A more recent method allows for achieving both the random access of records and a traversal through the records in sorted order. This method allows a more flexible use of the disk and guarantees excellent worst-case performance for a given number of records, with an acceptable amount of dedicated disk storage. It is known as the virtual sequential access method (VSAM). To see how it might be implemented, we study its basis B-trees. VSAM and many data base management systems use modified B-trees in their implementation. The basic reference for B-trees is the classic paper by Bayer and McCreight [1972]. Hash trees are an alternative to B-trees for the organization of large files of data. They are discussed and compared to B-trees by Bell and Deen [1984]. Tremblay and Sorenson [1984] discuss many file structure organizations. See Ullman [1982] for more on data base systems.
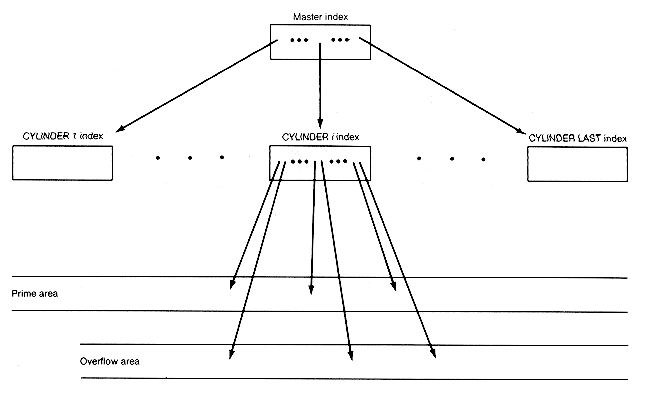
Figure 10.10 shows that the directories (the master index and the cylinder indexes) form a tree structure that guides the search for a record. Programmers try to find specialized trees leading to efficient searches, efficient use of storage, and relatively easy maintenance. Since the depth of the tree determines the worst-case search times, the goal is to find trees with short paths to terminal nodes. This implies that the nodes of the tree generally will have many successors. B-trees satisfy these requirements.

A B-tree of order m has the following four properties:
1. Every node of the tree, except the root and terminal nodes, has at least ?/FONT>1/2 m?/FONT> subtrees.
2. Every terminal node has the same depth.
3. The root node has at least two subtrees, unless it is a terminal node.
4. No node has more than m subtrees.
Each node of a B-tree will have the form shown in Figure 10.11. This represents storage for m - 1 keys and m pointers, although the storage may not all be used at a given time. If n is less than m, not all m keys are present in the node. Each pointer Pi points to a subtree of the node. The keys K1, K2, . . . , Kn are kept in sorted order, so K1 < K2 < ?/FONT> ?/FONT> ?/FONT> < Kn within the node. The subtree pointed to by Pi+1 contains all records of the file whose key values are less than Ki+1 and greater than or equal to Ki. P1 and Pn+1 point to subtrees containing records with key values less than K1 and greater than or equal to Kn, respectively. For example, if the keys are
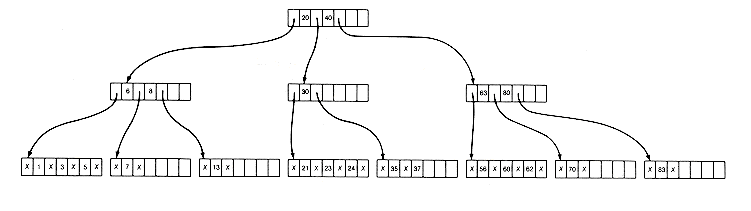
then the tree of Figure 10.12(a) is a B-tree of order 4 storing these keys and their records.
The terminal nodes of the B-tree in Figure 10.12 are not shown. Instead, the pointers to them have been replaced by null pointers. This reflects the way the tree might be represented in external storage. Notice that, in general, null pointers will appear at the same depth in the tree?/FONT>depth one less than the terminal nodes. A generalized inorder traversal (see Chapter 7) of the B-tree accesses the keys in sorted order. Associate with each null pointer the key value accessed immediately after the pointer is considered in such a traversal. A unique key is then associated with every null pointer except the last, and each key has a unique null pointer associated with it. For example, the first three null pointers have keys 1, 3, and 5 associated with them. The fourth null pointer (to the right of 5) has key 6 associated with it. Consequently, the number of null pointers, and the number of terminal nodes, is exactly one greater than the number of keys stored in the tree.
Any B-tree has a root node with at least two successors. Each successor has at least ?/FONT>1/2 m?I> successors. Thus there are at least 2 ?/FONT>1/2 m?/FONT> d-2 nodes at depth d > 3 of any B-tree. A B-tree of depth d > 3 has at least 2 ?/FONT>1/2 m?/FONT> d-2 terminal nodes, so
This implies that d < 2 + lgx?/FONT>(n + 1)/2?/FONT>, where lgx denotes logarithm with base x and x = ?/FONT>1/2 m?/FONT>. If n = 224 - 1 = 16,777,215 and m = 2 ?/FONT> 28 = 512, then (n + 1)/2 = 223, and lgx [(n + 1)/2] = lg256(223) < 3.
A B-tree storing 16,777,215 records will therefore have depth ?/FONT>4. We shall see that d - 1 is the maximum number of nodes that must be accessed when searching a B-tree for a search key. Thus we are guaranteed that no more than three node accesses are required to search for a key in the B-tree with 16,777,215 records!
A B-tree may be viewed as a generalization of a binary search tree, with a special imposed balance requirement to ensure against too great a depth. To search a B-tree for a search key value (say, 22) entails accessing its root node and traversing the node's keys until 22 is encountered, a key that exceeds 22 is reached, or the last key stored in the node is passed. If 22 is found, the search is complete. In Figure 10.12(a) the key value 40 is reached. The pointer to its left points to a subtree that must contain the search key, if it is in the tree at all. That subtree is then searched in the same way. Its root node is accessed, and 30 is reached. Following its left pointer, the final subtree root is accessed. Its key value, 23, is reached. Its left pointer is null, which means that the search terminates unsuccessfully.
Property 1 ensures that, except for the root and terminal nodes (which don't appear anyway), every node of a B-tree will be at least half full. Property 2 ensures that the B-tree will not be scraggly. All paths to terminal nodes must have the same length. The idea is to store information of a node on blocks of a cylinder on the disk, so that accessing a node requires one seek time and all keys of the node may be read into internal memory. The search through the keys of a node, to determine the next node to access, then takes place rapidly in internal memory, using an appropriate search technique.
After an insertion or deletion, of course, the tree must be maintained as a B-tree. This may be done making local modifications that are simpler than those required for AVL trees. For insertion, the key to be inserted is searched until a null pointer is to be followed. This assumes that only one record with a given key value appears in the tree and that it is similar to the initial insertion in AVL trees. If the node containing the null pointer has unused storage, then the key is simply inserted at the proper place in this node. This may require the shifting of keys in the node, but it is accomplished quickly in internal memory. For example, if key 35 is inserted in the tree of Figure 10.12(a), the result is the tree of Figure 10.12(b).
All insertions will be made in this way, in nodes at the lowest level, until the node becomes full. For example, if 28 is to be inserted next in the tree of Figure 10.12(b), no room exists in the node x 21 x 23 x 24 x . The m + 1 key values (the m old keys and the 1 new key) can be split by leaving ?/FONT>m/2?/FONT> - 1 in the old node and moving the remaining records, except the middle one, the ?/FONT>1/2m?/FONT>th, to a newly created node. The middle record is inserted in the predecessor (parent) of the old node. The result is the B-tree of Figure 10.12(c).
Had the predecessor been full, it would have been split in the same way in turn. Splitting may be necessary at every node of the search path, back to and including the root. If this occurs, the depth of the resultant B-tree is one greater than the original B-tree.
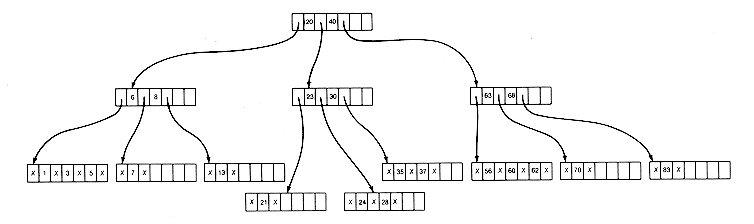
Deletion is done similarly. A key is simply deleted from a lowest-level node, and the keys shifted over, if the resultant number of keys satisfies the constraint that the node contain at least ?/FONT>m/2?/FONT> - 1 keys. If the constraint is violated, a key can be borrowed from a "neighbor" node, provided this may be done without violating the constraint for that node. In this case, the predecessor or successor key of the borrowed key moves into the deletion node, and the borrowed key takes its place in the predecessor node. For example, if key 7 is deleted from the tree of Figure 10.12(b), key 5 is borrowed from its neighbor (13 cannot be borrowed). The result is Figure 10.12(d).
If no neighbor can spare a key, the total number of keys between a neighbor and the deletion node will be less than m. These nodes may then be merged, along with a key from their predecessor. In the tree of Figure 10.12(d), if 83 is to be deleted, this situation will occur. The result is Figure 10.12(e).
It is possible for the predecessor to become too sparse, although this did not happen in our example. It is then treated as though its key were deleted, and so on, until the entire process is complete. This may go all the way to the root, in which case the root disappears and the depth of the tree decreases by 1.
If the key to be deleted were not in a lowest-level node, it would be replaced by its successor and the successor node treated as if the successor were being deleted.
These insertion and deletion procedures preserve the B-tree properties. The B-tree is an external memory data structure that plays the same role as AVL trees in internal memory. In practice, a modification of the basic B-tree is used to ensure better storage utilization and to increase the efficiency of traversal through the records in sorted order for VSAM. With B-trees the generalized inorder traversal must be used for sequential access. This is time-consuming and requires stack storage. Instead of storing some key records in higher-level nodes, the idea is to store all records only in lowest-level nodes and chain the lowest-level nodes by pointers. For example, in Figure 10.12(a) all nodes at depth 3 could be linked in a chain, with the leftmost node first and the rightmost node last on the list. A traversal then amounts to a traversal of this chain.
It is clear that storage management is needed for external memory, just as for internal memory. This problem is not discussed here, but the internal memory techniques are applicable, when properly modified to take into account the structure of the disks.
1,3,5,6,7,8,13,20,21,23,24,30,37,40,56,60,62,63,70,80,83
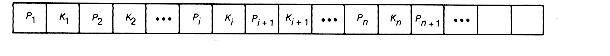
Figure 10.11 Form of Each Node on a B-Tree
n + 1 > 2 ?/FONT>1/2 m?/FONT> d-2

(a) Initial B-tree
(b) After Insertion of 35
Figure 10.12 A B-Tree of Order 4 with Twenty-one Records
(c) After Splitting, Due to Insertion of 28
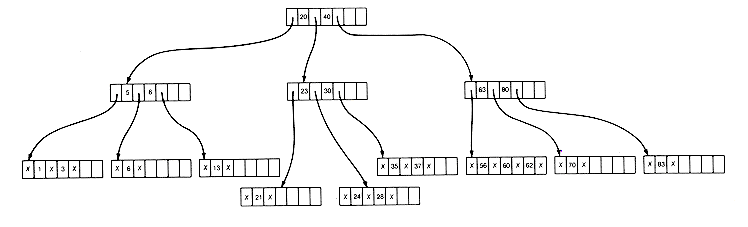
(d) After 7 is Deleted and 5 is Borrowed
Figure 10.12
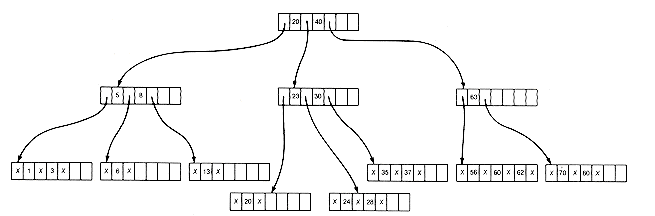
(e) After Deletion of 83 and Merging
Figure 10.12