1. Start with a collection of n trees, each with just a root. Assign an alphabetic character to each of these nodes. The weight of each node is the weight associated with its alphabetic character. The value of each of these root nodes is equivalent to its weight. (Value in this case equals the weight of the root itself, since these trees have no other nodes.)
2. Find the two trees with smallest values. Combine them as the successors of a tree whose root has a value that is the sum of their values. Remove the two combined trees and add the new tree obtained to the current collection of trees. Repeat the second step n - 2 times to obtain exactly one tree. This will be the optimal tree and will give the assignments of characters to terminal nodes.
When this algorithm is applied to the twenty-seven characters with their weights reflecting their frequency of occurrence in English, the first combination made is J with Q, since each has weight 1. The resultant tree has value 2. Next X and Z, also each of weight 1, are combined, yielding another tree with value 2. These two trees are combined, yielding a tree with value 4. The current collection now consists of twenty-four trees. The next combination involves weights 4 and 5 and yields value 9. Following this procedure, a final optimal tree that might result from the construction is shown in Figure 12.4. Other optimal trees could have been constructed, but all would have the same weighted path length of 5,124. This means that the average length (number) of 0's and 1's needed per character will be 4.124. The value 4.124 is obtained by normalizing the weighted path length (dividing it by the sum of the weights) and subtracting one. Thus 5124/1000 - 1 = 4.124. This saves almost 20 percent over a fixed-length code of length 5 (the shortest fixed-length code that can distinguish twenty-seven characters).
This construction procedure is the Huffman algorithm. A proof is given later showing that it does, in fact, produce an optimal binary tree. Notice that a cumulative total weight can be kept as the algorithm is carried out. To do this, start with the variable weight set at the sum of all the weights of the alphabetic characters. Every time two trees are combined, add the value of the resultant tree to weight. When the algorithm terminates, after making (n - 1) combinations, weight will contain the weighted path length of the optimal binary tree constructed.
The algorithm chooses the combination of current trees that yields a minimal value for the combined trees. It is in this sense that it is a "greedy" algorithm. It doesn't consider future ramifications of the current choice of subtrees to combine but takes the current two "best" subtrees. In this instance, best means "of smallest value." The algorithm makes a "local" best or greedy decision. It is an example of the greedy method of algorithm design, which involves making choices on the basis of the immediate best alternative. This may lead to later choices being constrained to such poor alternatives as to lead to an overall suboptimal result. Being less greedy now may lead to better choices later, which in turn may yield better overall results. Hence it is not obvious that taking the best possible next combination, as done here, must lead to an optimal tree.
The greedy method does not yield optimal solutions in all situations. A traveler who applied the greedy method to selecting a route might always choose the next road because it is the shortest of all the current possibilities. This method will clearly not always yield the shortest overall route. When making change in U.S. currency using our system of 1-, 5-, 10-, 25-, and 50-cent pieces and dollar bills, we normally use a greedy algorithm. For instance, to give $3.70 change most people would give three $1 bills, one 50-cent piece, and two dimes (not seven 50-cent pieces, one dime, and two nickels). The algorithm is greedy because it always takes as many pieces of currency of the next largest value as possible. This always minimizes the total number of pieces of currency used to make change in our system. If a system had 1-, 5-, and 11-cent pieces and dollar bills, then making change "greedily" to give $3.70 would require three $1 bills, six 11-cent pieces, and four pennies. Fewer pieces of currency result from using three dollar bills, five 11-cent pieces, and three nickels, Fortunately, the greedy method does yield optimal binary trees.
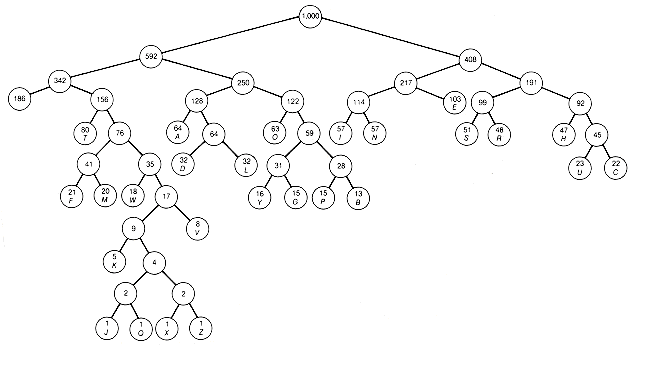
Figure 12.4 A Final Optimal Tree