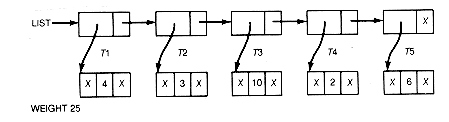
In this section the Huffman algorithm is implemented so that the Huffman tree and its weighted path length are generated. For a list of n records, a linked representation of the tree is illustrated in Figure 12.6(a) for n = 5 and weights 4, 3, 10, 2, 6.
The X's in the figure represent null pointers. The information field of each list record contains a pointer to a record representing the root of a binary tree. The records of the tree might be stored using pointer variables or in arrays. The records have leftptr, info, and rightptr fields. The info field contains the value assigned to the record's subtree by the Huffman algorithm. Thus each list record represents a tree. Weight is a variable initially set to the sum of the n weights and incremented by the value attached to each combined tree.
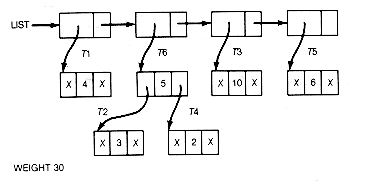
The implementation could proceed by traversing the list to find the trees with the two smallest values. These trees must be combined as dictated by step 2 of the algorithm into a new tree whose value is the sum of their values. The two trees that were combined must be deleted from the list, and the new tree added to the list. The result of these operations is shown in Figure 12.6(b) after one combination has taken place.
Every time step 2 is repeated, two trees are combined and the length of the list decreases by 1. The final list would contain one record; its information field would point to the root of the generated Huffman tree. Weight would contain its weighted path length. For this example, the resultant list would be as shown in Figure 12.6(c).
The list traversal required to find the two smallest value trees results in a worst-case time proportional to the length of the list for each traversal. Since the tree must be traversed n - 1 times, the worst-case time is O(n2). We can do better.
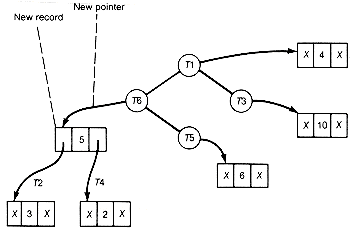
To improve the implementation, the two smallest values whose trees are to be combined must be found quickly without traversing the entire list. Recall that a heap, in this case a min heap, always has its smallest record at its root. Suppose the records of the binary tree are kept in a heap, or better, suppose the pointers are kept in the heap. Each pointer points to a corresponding record of the binary tree. The initial heap is shown in Figure 12.7.

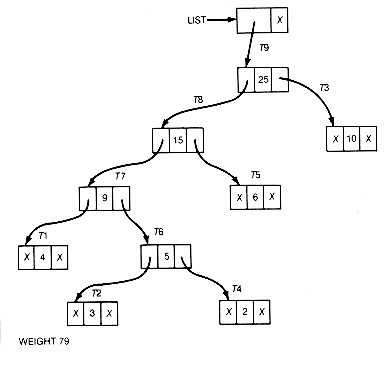
To find the two smallest values, simply remove the top heap pointer T4, reheap, and again remove the top pointer, T2. The records corresponding to the two smallest values can be combined. The new pointer to the combined record can then be placed at the top of the heap (which was left vacant), and the heap reheaped. Figure 12.7(b) shows the heap obtained by removing T4, reheaping, and removing T2. The two trees removed are combined, and reheaping is done to obtain the heap shown in Figure 12.7(c).

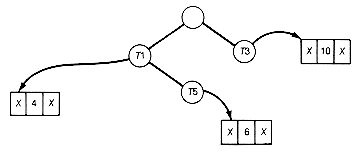
With this implementation the computer time consumed in finding the two smallest values, combining their corresponding records, and reheaping is O(lg n). Since the entire process is repeated (n - 1) times, the total time will be O(n lg n). It was the proper choice of data structure that made this improvement possible!