10.2: Internal and External Memory
Computer memories are normally thought of as falling into two basic categories, internal and external. Which memory is used to store data depends on the trade-off of efficiency of access to data versus the cost of that efficiency.
The data structures and algorithms considered thus far are all appropriate to the internal memory of a computer. This memory is also referred to as main memory or random access memory. A program can process only information stored in its internal memory. If the program is to process information stored in external memory, that information must first be read into its internal memory. Except for the instructions involved in this transfer of information, all program instructions refer to variables that name internal memory locations.
By means of random access, it is possible to access any individual internal memory element in exactly the same length of time--typically one-millionth of a second or less. This access time is independent of the past history of accessed elements. However, random access memory is expensive and, although available in increasingly larger sizes, is still relatively small in size compared to the storage needs of many applications.
External memory, also referred to as secondary storage, is so called because it is physically outside the computer itself. It is relatively inexpensive and is available in very large amounts, but access to an arbitrary record is slow compared to internal memory. Magnetic tapes, floppy disks, and magnetic disks (also known as hard disks) are the usual devices for external storage of data. The characteristics of these devices that are essential for efficient use of data structures are discussed in this chapter. Since the characteristics of secondary storage devices are different from those of internal memory, the data structures and algorithms required to process the data they store are distinct from those for internal memory. However, many of the same concepts and techniques of good design and implementation of algorithms are still applicable and form the basis for representing and operating on information stored in external memory.
Programming languages such as C do not ordinarily allow direct manipulation of external storage elements. Instead, as with internal storage, they provide commands that allow programmers to deal with external memory conceptually. C provides very limited kinds of operations to be performed on its conceptual external memory, whereas COBOL provides very extensive operations. FORTRAN falls between these extremes. Whatever high-level language is used, the operating system of a computer installation provides commands to make files available for processing by a program. Operating systems allow permanent storage of files generated by a program during its execution. The stored files can then be retrieved for later use.
You may have used the DOS, MVS, VM, or NOS operating system on a mainframe computer; RT-11, RSTS, RSX, TSX, VAX/VMS, or UNIX on a mini-computer; or MS-DOS, PC-DOS, UNIX, or CP/M on a micro - or personal computer. In effect, operating systems provide repositories of files that may be added to, or referenced by, programs. Such files are used to store data or information to be processed. They are also used to store algorithms (such as programs to be executed), data base management systems to organize and maintain large data bases, compilers to be invoked, or even other operating systems to be used when needed. Thus operating systems support the development of libraries of data and algorithms that programmers use, add to, or delete from. They support the general programming strategy recommended and demonstrated in this book; in solving a problem, the programmer begins by attempting to apply an already known algorithm, either directly or after appropriate modification.
Frequently, a solution to a problem is readily found by starting with one or more files of data and repeatedly applying available programs to these files. These programs, in turn, produce output data in the form of files, which then become the input files for other programs. The basic idea behind this kind of solution is a filter--a program whose input is one file and whose output is another file. A solution to a problem may often be found by starting with an input file and applying a sequence of filters. Each filter takes as its input the output file of the preceding filter. System commands allow this composition of filters, so that complex programs can be generated with few commands.
Example 10.1
Suppose an input file contained the roll scores for the bowling problem of Chapter 1. The problem is to structure the solution so that processing this file produces an output file of statistics.
Suppose gamescores is a filter that takes the input file and produces an output file of game scores. Once the game scores are available, a statistical package in the computer's operating system library might be used to process the game scores as an input file (as data), producing appropriate statistics. Applying this program, or filter, to the game scores file would result in an output file containing the required information. This file could be stored for future use or processed by a printing routine, producing printed output directly.
The two filters, gamescores and statistics, applied sequentially, produce the desired output file. Note that this solution is written so that the calculation of the game scores is done first, independently of the calculations producing the statistics. In the solution of Chapter 1 these tasks were intertwined.
The idea behind filters is to allow the construction of complex programs by sequencing simpler but powerful programs. The next example illustrates this more forcefully.
Example 10.2
Use filters to produce a simplified index for a book. The index should consist of the important words of the book in alphabetical order and the pages on which they appear.
One way to achieve a solution is to apply the following filters in sequence.
1. Word-count references
2. Truncate
3. Sort
The first takes a file consisting of the book text (organized as a sequence of pages) and produces an output file of records. Each record contains a word or sequence of words, the number of pages on which it appears, and the pages on which it appears. Truncate takes a file of records as its input and outputs a file that is identical to its input file, except that all records with a designated key field value greater than n are deleted. The key field contains the number of pages on which the word or sequence appears. A reasonable value for n might be 10. This should eliminate frequently occurring but not relevant words such as "the," "a," "and," and so on. Sort takes an input file of records and creates an output file in which the records appear in sorted order by designated key field value--in this case, the word field. The sequencing of these three relatively simple filters provides a quick and effective solution.
Using these system capabilities to store and access files of data or programs provides a framework in which to approach the entire task of problem solving. In effect, a computer installation provides a programming environment that determines the tools available for program construction. Such tools include text editors, data base management systems, file management utilities, ways to create a new program from existing programs already stored as files, and debugging aids. The enhancement of such programming environments is currently one of the major research and development areas of computer science. The command languages, also known as job control languages, provided by operating systems are used to operate on general files.
During the execution of high-level language programs, operations typically deal only with files treated as data. Operations include traversing and processing all the records of a file, randomly accessing and processing individual records selected in random order, or some combination of these two modes. The basic function of a file system, in addition to providing storage facilities, is to allow files to be searched efficiently and conveniently, so that records of an entire file may be sequentially retrieved or a portion of the file's records (perhaps only one record) may be randomly retrieved. In Example 10.1, after the bowling game scores file has been obtained, one may want to retrieve the scores of a particular game or individual.
This chapter briefly discusses the file processing facilities provided by C. It shows a number of ways in which more flexible and powerful file processing may be implemented. The literature on files would itself require a large file for its storage, and file storage and manipulation is currently an active area of research.This book considers a very small portion of that activity. The discussion deals only with the case of fixed-length records that are to be retrieved on the basis of a single field value, the primary key field. A primary key uniquely identifies a record. It is the field normally used as the search key, and the key by which records are sorted.
Just as with data structures that are stored in internal memory, the programmer must take great care to keep related records of files stored in external memory physically contiguous or linked by pointers. In internal memory, the time requirement of an algorithm is measured by the number of operations performed. These might be arithmetic operations or assignments, comparisons between two records (keys), or comparisons between two variables. When dealing with external memory, the time requirements are measured by the number of accesses to secondary storage.
C has no built-in ability to perform input/output. Input/output is done by using the standard C library <stdio> or by developing a user library. The printf and scanf functions used in the programs of the book are in this standard library.The <stdio> library contains a number of other functions that also perform input/output.
C input/output is character-oriented. All reads or writes to or from keyboards, screens, tapes, or disks are character-oriented. C reads or writes in bytes.The functions that read or write numbers or strings in turn use calls to the basic character-oriented input/output functions.
There are two ways to read or write files in C. They are termed high-level and low-level input/output. In high-level input/output, reading and writing is done a character at a time. The input/output is buffered, and the programmer does not have to consider buffer sizes or other characteristics of the operating system. The buffers, however, are not available to the programmer. In low-level input/output, which is essentially UNIX-type input/output to provide a UNIX interface, the buffers are not provided; the programmer must provide buffers and pointers to control the input/output process. In the following discussion only high-level input/output will be considered.
The simplest organization for a file is sequential. A sequential file is a sequence of records. The records may or may not be kept in sorted order in the sequence. In standard C input/output all files are sequential files. A record of a file is not necessarily declared to be of type structure. Although file records are typically of type structure, a file record may also be declared to be of type integer, float, character, or any other C type. All records of a file need not be the same type.
Example 10.3
To illustrate how records composed of structures are treated, suppose you are asked to keep a master file, bookinventory, consisting of records representing all books currently in stock in a book store. Each record is to contain a title, author, publisher, price, and currentstock field. These declarations may be used:
The name of a file is a variable within a C program. Unlike other variables, it represents stored information that may have been available before the execution of the program or that may be available after the execution of the program. A file named f is depicted in Figure 10.1.
Associated with each file is a file pointer, which always points to a record or is positioned prior to the first record or after the last record. File pointers must be declared and are of type FILE. For example,
declares f_ptr as a file pointer.
A record may be read from a file or written to a file. A read or write statement refers to the record indicated by the current position of the file pointer. Each file also has a portion of main memory, called the buffer, associated with it. When the file pointer is pointing to a file record, the file buffer contains a copy of that record's contents.
To attach a file to a program, it is necessary to execute an open statement. For reading the records in the file containing the bookinventory records, the following code is used.
F_ptr is the pointer to the file bookinventory. The r signifies that the file will be opened for reading only and that the file is already in existence.
Executing the first statement causes the file pointer f_ptr to be positioned to the first record. If any error occurs and the file can not be opened, the file pointer will returns a NULL value. For this reason, it is a wise policy always to test for the NULL pointer when opening a file, as was done above.
If the open is executed with a w (instead of an r) it opens the file for writing. If no file by the name used exists, it creates a new file and places the file pointer at the beginning of the file. If a file already exists, it places the file pointer at the beginning of the file, in effect erasing or truncating the file. If a file is opened with an a, it creates a new file or, if one already exists, positions the pointer at the end of the file for appending items. A similar set of values, r+, w+, and a+ is used to open files for both reading and writing.
To read a single record or numbers of records from a file the fread( ) function is used. The general form is
For example, to read a single record from the opened file:
Executing this statement will cause the value of the record pointed to by the file pointer to be copied into memory starting at the memory location pointed to by &bookinventory. Also, fread returns the number of records read, or zero when the end of file is reached.
To write a record to a file that is open for writing:
Executing this statement will cause the value of the record starting at the location pointed to by &bookinventory to be copied into the storage pointed to by the file pointer, and the file pointer moved to point to the storage to be used for the next record.
Reading from a file thus causes information in secondary storage (the file) to be transferred to variables whose values are stored in internal memory. Writing to a file causes the information stored in internal memory to be transferred to secondary storage.
Example 10.4
To illustrate how files composed of single variables such as integers are treated and the effect of the file operations, consider the following program. The file prime will be created initially to consist of the first 10 primes. Note that the reading and writing are done with fscanf and fprintf. They are like scanf and printf except that they work on files of individual variables. In contrast, fread and fwrite work on files of records. Also, fscanf returns EOF when the end of the file is reached or an error occurs.
Prime and reversedprime are files of integers and a is an array of integers.
After (1) fopen is executed, the file called prime and its file pointer can be depicted as in Figure 10.2(a). After nine executions of the first while loop body, the situation will be as shown in Figure 10.2(b).
The tenth execution sets a [9] to 29 and moves the file pointer beyond the last file record. The EOF test yields the value true, so the loop is exited with i set at 10.
After (2) fopen is executed, reversedprime appears as in Figure 10.3(a). After the second while loop body has been executed nine times, reversedprime looks like Figure 10.3(b). The last execution yields the file shown in Figure 10.3(c).
The standard function, exit, closes any open files, flushes any buffered output, signals what has happened, and terminates program execution. A zero parameter value, by convention, signals that all is well, while other values may have different meanings. The -1 is used here to signal that a file could not be opened. Files can also be closed by simply invoking the function fclose, whose parameter is the file pointer of the file to be closed. It is important to close all files appropriately.
Suppose you wished to append the eleventh prime, 31, to prime after 29. This can be done directly in C by opening the file prime to its end so that items can be appended. To do this, as noted earlier, the file need only be opened with the a to position the file pointer
Example 10.5
Suppose there are two files with records of the same type in sorted order based on key value. Merge the two files.
Producing a new file consisting of all the records of the two files in sorted order is called merging the two files. The merging of two files is a basic component of efficient methods of external sorting. The task in Example 10.5 is to write a function to produce a merged file assuming records are ordered with the smallest key value appearing in the first record.
The basic idea is straightforward. Read a record from each sorted file, and append the record with the smaller key value to the merged file. Read the next record of the file that had the record with the smaller key value. Compare it with the record that has not yet been appended. Append the record with the smaller key value to the merged file. Repeat this process of reading and comparing records from the two files until one of the files becomes empty. Then append the records on the remaining file to the merged file.
Assume that the files to be merged are not empty and have been opened with filepointers f1_ptr,f2_ptr, and f3_ptr. Filepointers f1_ptr and f2_ptr point to the input files to be merged. Filepointer f3_ptr points to the resultant merged file. The files are made up of records of typedeffilerecords, with key the field of filerecords on which merging is to be based. The merge may be written as follows:
The files must be opened before the merge is invoked.
The following program, when the merge is included, merges two files and prints the resultant file.
A range of devices is now available for use as secondary storage, the most common being magnetic tapes and disks. Tape cassettes like those used with stereo equipment are prototypical of the magnetic tape used for secondary storage. If a song is being played on such a tape, the time required to access another song on the tape depends on how far away from the current position that song is. This accessibility is the same for magnetic tapes used as secondary storage. Such a tape can be pictured as containing a sequence of fixed-length blocks (Figure 10.4). Each block contains a fixed number of records of a file (say, n per block). One or more input buffer areas (reserved storage areas) are set aside in internal memory, each large enough to hold one block of records. These buffers are required in order to allow for efficient reading and writing of files.
Suppose one buffer is set aside. To read a block of records into the buffer, the tape must be moved at sufficient speed past a read head. This speed determines the rate at which data are transferred to the buffer. If a sequential file is stored on magnetic tape, executing the open statement causes the buffer storage to be allocated, the tape to be rewound so that the first block may be read, and the first block to be read into the buffer. After these operations have occurred, the buffer and the file pointer can be visualized as in Figure 10.5.
If a read is executed, the first record is copied from the buffer into its memory location, and the file pointer is advanced to the next buffer position. Consecutive executions of a read for this file cause similar actions. Finally, when n such reads have occurred, the next block of records from the tape is placed into the buffer, the file pointer is automatically repositioned at the first record of the buffer, and the process is repeated. Had two buffers been set aside, as the current buffer is being read the other would be filled with the next block of file records. A similar procedure takes place for the writes with respect to an output buffer for the file. In this way the buffer is being filled, when reading from a file (or emptied, when writing to a file), at the same time that the computer is carrying out other commands of a program. Record blocking is done because n records can be read or written as a block much faster than individually, since it reduces tape starts and stops. Today's computers, whether mainframe or personal, can execute on the order of 100,000 commands in the time it takes for a block to be read into or written from the buffers. A program may actually process n records of the file while the next block is being transferred to the buffer. For example, the records may be sorted or individually processed during this transfer time. In this case, the time required to process the entire file is determined by the time required to scan the file in this fashion. Thus the number of accesses to secondary storage determines the execution time of the program. This may take minutes, which is a very long time in computer terms.
It should now be clear why sequential files should not be used when records must be accessed in an order other than the order in which they appear on the file. Attempting to access the records in random order may mean spending great amounts of computer time, since minutes may be required for each access. Instead, the typical use for sequential files is when records are to be processed in turn, starting from the first record. In other words, when the processing to be done can be accomplished by a traversal through the records of the file, then sequential files are appropriate. This is typical of external sorting, copying, updating, and printing (such as end-of-the-month billings).
As a practical example, suppose you are given the master file, bookinventory, of Example 10.3, and another transaction file, booktransactions. Booktransactions consists of records representing the arrival of new books for inventory and the sales of books in the last week. If both files are sorted on the same key (say, title), it is possible to traverse each of the files once and update each master file record to reflect new arrivals and sales. A new file must be created for this updated master file. This step would actually be advantageous for security purposes, since the old master file and booktransactions file could be saved. If anything were to happen to the new master file, the procedure could be repeated and the file reconstructed.
Once again, one picture--or in this case, a good example--is worth a thousand words. The different merging techniques demonstrated for the following example illustrate some of the complexities of sorting files stored on magnetic tape, when all records of the file cannot fit into internal memory at the same time. Tape sorts are used here, since they highlight the concepts of sorting, but these concepts are also applicable to disk sorts. Detailed analysis of the sorting algorithms discussed here, and others, may be found in Knuth [1973b]. We begin with an extreme case.
Example 10.6
Sort an original file of twenty-one records that are stored sequentially on a tape file. The records have integer key values. Assume that only two records can be kept in internal memory at any one time. Storage for the two records is in addition to input and output buffers.
Suppose the sequence of records in the original file is as follows:
It is not possible simply to read all the records into internal memory and then apply one of the internal sort algorithms of Chapter 8, since available internal storage is assumed to be only enough to hold two records. Instead, the general strategy, given that two sorted files can always be merged as shown in Section 10.3, is to create sorted subfiles repeatedly and merge them repeatedly until a final merged file containing all the original records is produced. The literature contains many ingenious algorithms for external sorting. This chapter gives only the flavor of the solutions. One major constraint on a solution is the number of tapes available for use in the sort. Assume three available tapes.
Perhaps the most straightforward sorting technique is the straight merge. The straight merge distributes the initial records onto two tapes, a and b, so that they contain the same number of records, or so that one tape contains only one more record than the other. If this is done for the original file in Example 10.5, then the configuration of tapes a and b will appear as the initial distribution.
Now a and b can be thought of as being composed of subfiles, each of which is sorted and of length 1. A subfile is a run of length r if it consists of r records sorted in order. Here, a contains eleven subfiles, or runs, of length 1, and b contains ten runs of length 1.
Apply a merge procedure to each pair of runs, each pair containing a run from tape a and the corresponding run from tape b. Thus
are "paired." The merge procedure consecutively merges each pair (consisting of a sorted subfile of length 1 from a, and a corresponding sorted subfile of length 1 from b). The resultant merged files are written consecutively to tape c. The result of the first merge of a and b to c is
Think of c as containing ten subfiles or runs of length 2 and one run of length 1 and distribute these to a and b equally to obtain the second distribution.
By now there are five paired runs of length 2 and one run of length 1. These may again be consecutively merged, and written to c to obtain the second merge of a and b to c.
Another distribution to a and b yields the third distribution.
These pairs of length 4 can now be merged to obtain the third merge of a and b to c.
It takes two more distributions and merges to complete the sort. The fourth distribution
is followed by the fourth merge.
The fifth distribution is next. It is followed by the fifth merge.
This completes the sort, which has taken five distributions and five merges. The sort is described as a five-pass sort, with five distribution phases and five merge phases, using three tapes. Programming this process is not a trivial task. Ignoring details, the basic time requirements can be seen to be determined by the number of times files must be rewound or rewritten and the number of records that must be accessed from secondary storage (tapes). This assumes that the internal memory processing will be done so quickly that it does not add to the total time for the sort. Before the original file, c, can be distributed (rewritten) to tapes a and b. those tapes must be rewound and the original file must be rewound. Before a and b can be merged (and written) to c, they must be rewound, and c must be rewound. Also, in each phase, whether distribution or merge, each record must be accessed from secondary storage. Thus the total time is proportional to the number of passes (five here). If the access time of a record is Ta, and the rewind time Tr, then the total time is 5 X (2 X 21 x Ta + 3 X Tr). Note the factor of 2 associated with the twenty-one records and the access time. The factor is 2 because there are two phases, distribution and merge.
The straight merge sort does not take advantage of any natural ordering that may exist in the original file. Even if that file were given in sorted order, the straight merge would proceed as before. A natural merge sort distributes the records of the original file to a and b, so that sorted subfiles or runs are preserved and treated as a unit. Such a distribution would assign 2 12 17 to a, since they form a run. The 16 terminates this run and goes to b. The 14 terminates this run and goes to a as the beginning of its second run, followed by 30. So far the result is
The 17 now terminates the 14 30 run and goes to b. Note that this extends the first run of b to 16 17. At this point, 2 terminates this run with the following result.
If balance is to be maintained, each file must end up with a number of runs differing by no more than 1 from the other files. Therefore the next run (starting with 2) must go to b. Subtleties of this kind must be carefully monitored in the actual implementation of merge sorting algorithms. The resultant distribution will be the initial distribution.
Merging these pairs of runs and writing the merged results to c yields the first merge.
Another distribution and merge gives the second distribution,
which is followed by the second merge.
A third and final distribution and merge complete the sort. The third distribution yields
The result of the third merge is as follows:
This is a three-pass, two-phase sort, using three tapes. The total time is 3 X (2 X 21 X Ta + 3 x Tr). Any inherent ordering of the initial data allows the number of passes to be reduced, as compared to the straight merge sort.
Note that to merge runs embedded in a file, the procedure of Section 10.3.1 requires modification.
Since there is typically room for a reasonable number of records in internal memory, both the straight and natural merge sorts can be speeded up. For instance, if m records can be sorted in internal memory, the straight merge sort can start with the distribution of runs of length m on each of the tapes a and b.
There is a clever way to produce runs for distribution (for example, with the natural merge sort) without actually storing the m records. This is the replacement-selection sort, which uses a heap of size m and works as follows. Start with the first m keys of the original file of Example 10.6 in internal memory and create a heap to obtain Figure 10.6(a) (m = 7).
Remove the root key from the heap and output it to an output file. The next input file key, 2, is inserted at the root of the heap, and the heap is reheaped, giving Figure 10.6(b).
Again, the root key is removed and written to the output file. The next record key of the input file, 50, is inserted at the root and reheaping occurs. Figure10.6(c) results.
Continuing in this way generates a run on the output file of length 8, which would be terminated when 16 from the input file is inserted at the root of the heap. The situation at that point is shown in Figure 10.6(d). Instead of terminating the run at length 8, treat 16 as associated with the next run, since 16 is less than the last output value, 20. This means that 16 must be distinguished from the heap entries for the current run; it is shaded in Figure 10.6(d). In reheaping, current run entries are considered smaller than next run entries. Figure 10.6(e) shows the heap after reheaping. Each input smaller than the last output is handled in this way. Eventually the heap becomes filled with entries of the next run, and the process repeats.
Notice that the length of the output run will always be at least m (with the possible exception of the last run generated). Continuing this process, called replacement-selection, we obtain the output file,
The original file consisted of ten runs; the output file after replacement-selection consists of two runs. With randomly ordered input files, this replacement-selection generates runs whose average length is 2m. The example exhibits this behavior in an exemplary fashion.
Notice that both the straight and natural merges spend half their time accessing records for the distribution phase. Spending this time can be avoided by using another tape. By this technique, each time two runs are merged, they can be written, alternately, to tapes a and b. This eliminates the need for extra, basically unproductive, time spent in distribution from tape c.
Rather than using more tapes, it is possible to incorporate the distribution phase (except for the initial distribution) into the merge phase. Such a sort is called a polyphase sort. In this type of sort, the tapes being merged, and the tape to which the merged subfiles are written, vary continuously throughout the sort. In this technique, the concept of a pass through records is not as clear-cut as in the straight or the natural merge. A distribution, a merge, and a pass all blend together. This might have more properly been called an amorphous sort, except that it has considerable character and is one of the better sorts.
The polyphase sort starts with an initial distribution of runs on tapes a and b. The initial distribution is critical to its proper execution. For the case of the original file of twenty-one records in Example 10.6, the initial distribution should be thirteen runs to tape a, and 8 runs to tape b, each of length 1. It is the number, not the length, of the runs on each tape that is critical. The number of records for the example is twenty-one because the first few Fibonacci numbers are 0, 1, 1, 2, 3, 5, 8, 13, 21. The Fibonacci numbers are crucial to the polyphase sort because the number of records must be a Fibonacci number to make the polyphase sort work.
When a three-tape polyphase sort is used, the original number of runs should be a Fibonacci number, with the distribution of runs between tapes a and b the two preceding Fibonacci numbers, which add to the original number of runs. In the present case, 8 + 13 = 21. When more tapes are used, generalized Fibonacci numbers, which specify the required number of records, become the basis for the initial run distribution among the tapes. No programs will be shown for the implementation of the details of the external sorting algorithms discussed in this section. Therefore it is unnecessary to resolve in detail the question of how to proceed when the actual number of runs is not a Fibonacci number. The remedy, though, involves adding an appropriate number of "dummy" runs [Knuth, 1973b] .
Getting back to the workings of the polyphase sort, the initial situation after distribution will be an initial distribution.
This distribution required twenty-one record accesses.
We now proceed by merging the first eight runs of a and the eight runs of b to c to obtain the merge of the first eight runs of a and b to c.
Notice that b is now empty, a total of 8 + 8 = 16 records have been accessed, and a and c contain 5 + 8 = 13 runs. All three tapes had to be rewound before the initial distribution, but only b need be rewound now. It is possible to continue merging the first five runs of c and the five runs of a to b. This results in a merge of the first five runs of a and c to b.
Notice that a is empty, a total of 5 + 5 X 2 = 15 records have been accessed, and b and c contain 5 + 3 = 8 runs. Tape a is now rewound, and the first three runs of b are merged with the three runs of c. The result is the merge of the first three runs of b and c to a.
Tape c is now empty and must be rewound. A total of (3 X 3) + (3 X 2) = 15 records were accessed, and a total of 2 + 3 = 5 runs remain. Merging the first two runs of a and b to c yields
This leaves b empty, so we rewind it. A total of (2 X 3) + (2 X 5) = 16 records were accessed, and 1 + 2 = 3 runs remain. Merging the run of a and the first run of c to b yields.
A total of (1 X 5) + (1 X 8) = 13 record accesses occurred, and 1 + 1 = 2 runs are left. Tape a is rewound. Then a final merge produces
This final merge of b and c to a took 13 + 8 = 21 record accesses. A total of 117 ( = 21 + 16 + 15 + 15 + 16 + 13 + 21) record accesses is required. These 117 record accesses represent an effective 117/21, or 5 4/7, passes. The total time for this algorithm is 117 x Ta + 8 x Tr. The straight merge sort and the natural merge sort required 210 X Ta + 15 X Tr and 126 X Ta + 9 X Tr time, respectively.
The polyphase sort, until completion, results in exactly one empty tape, so that the remaining tapes may be partially merged to it. After each merge, the distribution of runs is made up of two consecutive Fibonacci numbers (13 + 8, 8 + 5, 5 + 3, 3 + 2, 2 + 1, 1 + 1, 1 + 0) . With more tapes , this is also true , but generalized Fibonacci numbers appear.
Accessing a song on a phonograph record is different from accessing a song on a tape cassette. Think of the songs as stored along the grooves of a record rather than along the tape of a cassette. Instead of going through each song between the current arm position and the location of the desired song (and scratching the record!), the arm is moved directly to the proper groove. Once the arm is placed, it is necessary to wait until the record revolves, so the beginning of the song appears under the arm. The movable arm eliminates the need to pass through all songs that intervene between its current and desired positions. The magnetic disk works the same way. It is the reading head that moves to the desired storage location, thus saving access time compared to the magnetic tape.
Magnetic disks and disk packs are examples of direct access devices used for secondary storage. In this context, direct access means that a program can go straight to desired information stored on a given surface and cylinder. This access time is not constant. It is slower than random access in internal memory, but generally much faster than the sequential access time for tapes. A floppy disk has similar access capability but is slower and has much less storage capacity. Thus in terms of access time, direct access storage devices fall between sequential access devices, such as magnetic tapes, and random access memory. Hard disks are generally used with mainframes and minicomputers, whereas microcomputers or personal computers vary from no disks through floppy disks to hard disks.
A random access memory allows very fast access to any element of the memory. The access time is the same for all stored elements, no matter which element was last accessed. Sequential devices allow fast access "locally," but all elements between the currently accessed element and the next desired element must be passed through before the next element may be accessed. Consequently, the time to access the next desired element is proportional to its distance from the currently accessed element. Direct access devices are intermediate between these two extremes. They act like sequential devices with tabs. Just as using the alphabetical tabs in a dictionary allows a person seeking a word to find it quickly, so do "tabs" allow one to close in, relatively quickly, on the desired area of the sequential storage. In direct access devices, the "tabs" are the movable read/write heads.
Sequential devices are convenient for tasks that may be accomplished by traversing records. However, when the order in which the records must be processed cannot be predicted, sequential access devices are not efficient. Tasks requiring random access to records cannot be accomplished efficiently using sequential memory devices. The introduction of economical direct access devices made random access feasible. As a result, airline reservation systems, interactive computing, and instant updating of bank accounts have become commonplace. This was made possible by the development of appropriate technology for direct access memory.
A magnetic disk is a flat, circular platter on whose surfaces information can be stored and accessed. It can be pictured as a phonograph tone arm and record, with its concentric tracks corresponding to the grooves of the phonograph record and its movable read/write head corresponding to the tone arm. A disk pack consists of a pile of such magnetic disks and a read/write head for each record surface--that is, one head for each side of a record (see Figure 10.7). The read/ write heads are typically coupled so that they all move at the same time. They are positioned over the same track on their respective surfaces, although only one head is actually reading or writing at any moment. There may be twenty magnetic disks and a hundred tracks on each disk.
Each track of a surface in a disk pack stores records in blocks, similar to the blocking of records on magnetic tapes. Each track behaves as a sequential access device, like a magnetic tape. That is, each block must be passed through, as the disks rotate, before another block farther along the track can be accessed by the surface read/write head.
If we focus on the same track on each surface, then the pile of tracks forms a conceptual cylinder in space, as shown in Figure 10.8. Assuming tracks are numbered (say, from 1 to 100), a cylinder consists of all tracks with the same number. Thus the disk pack can be viewed as composed of one hundred concentric cylinders.
A cylinder is important because it allows any block of records stored on a surface of the cylinder to be accessed without moving the read/write heads. Accessing a block stored on a different cylinder (or track) requires moving the read/write heads. The time required to move the heads from one cylinder to another is called seek time; it is proportional to the distance between the cylinders. This time typically takes a significant fraction of a second (1/10th to 1/20th). It is the dominant factor in dealing with time requirements for accessing blocks on magnetic disks.
Once the read/write heads are positioned over the desired cylinder, the time required for the desired block to rotate under the heads is called latency time. It can be on the order of one hundredth of a second.
Often large amounts of information, too much to fit into internal memory, must be organized so that random requests for specific pieces of information can be readily satisfied. The methods of organization that are useful in internal memory are not adequate for data stored on disks in external memory.
There is a natural way to store records sequentially on magnetic disk to minimize total seek time for a traversal through the records. This storage technique is based on the cylinder concept. It starts by filling blocks of the top surface track of the outermost cylinder with records. The records are in sequence within the blocks. When the track is full, the same process is repeated with the track of the next surface, and the next, and the next, until the lowest surface track is filled. At that time the outermost cylinder has been filled. Continuing in the same way, records are stored on each of the inner cylinders, starting with the next adjacent cylinder. This is similar to storing records sequentially on magnetic tape. In fact, we can picture the surfaces and cylinders laid out linearly as in Figure 10.9. This arrangement has all the inherent drawbacks of magnetic tape, whenever random accessing of records is required.
We can adapt disk storage to random accessing by taking advantage of the tab feature of the disk, which allows the head to go directly to any cylinder and surface. The problem is how to determine exactly where to go. If one knew that the record to be retrieved were the ith record, then it would be easy to calculate on which cylinder and surface it would be located. This is not often the case, since the search is conducted by means of key value, not by order in the sequence.
A linear search of the file could be done but might take O(n) time, when n records are stored in the file. This could take minutes. If the records are stored in sorted order by key value, a binary search of the file might be done. The difficulty here is that 1g n accesses are required. A million-record file would require twenty accesses, and each access might require a seek. While the binary search is better, it still might take seconds. This is reasonable for isolated requests, but during this time there may be many requests for desired retrievals. Waiting requests may build up interminally, with unlimited waiting time before all are processed. The need to insert or delete records further compounds the problem.
Just as in the case of internal memory, keeping records in blocks with pointers to succeeding blocks is a possibility, based on the concept of lists. This may avoid insertion and deletion difficulties, but it does not alleviate the problem of searching. We encountered this same problem with lists in internal memory. What about binary search trees? Even if balanced, a million records may need as much as 20
We still have hash tables in our arsenal. Using hash tables in secondary storage requires some accommodation to its access capabilities. Buckets, an extension of the chaining policy for collision resolution with internal memory, are appropriate. The idea is to create a hash table based on key values. The hash table will contain pointers to lists. Each list, referred to as a bucket, contains all records that hash to the same hash table address. The lists are stored in blocks on the disk, each block holding a fixed number of records and a pointer to the next block containing other records on the list. When a key is inserted into the hash table, the program determines its hash address and then inserts the key into the bucket pointed to by that address. The key may be inserted into the bucket by traversing the list of linked blocks until a block is encountered with room for the record. If no such block is found, a new block is appended to the list, and the record is inserted in that block. Care must be taken to avoid wasting seek time (and latency time) when these lists are being traversed. This means that the blocks of a bucket should be on the same cylinder. Searching for a key is similar to making an insertion. Deletion involves the usual deletion from a list, with care taken to release unneeded blocks when possible. When small enough, the hash table itself is kept in internal memory to avoid one disk access.
In practice, such hash tables can be devised so that one or two disk accesses are required for either successful or unsuccessful searches. This is accomplished by selecting a good hash function, an appropriate fixed number of records per block, and an appropriate number of buckets. The usage factor of such a hash table is given by n/bk, where n is the number of records stored, b is the number of buckets, and k the fixed number of records per bucket. If the performance of the table degrades as insertions are made, the table may be reorganized.
Other interesting and important external hashing methods are presented in Larson [1976], Litwin [1960], and Fagin, Nievergelt, Pippenger, and Strong [1979].
While the hash table solution may yield fast average access times, there is no guarantee for the worst case, nor any convenient way to access records in sorted order by key value. To achieve the ability to access records in random order or in sorted order, as necessary, we must incorporate an old idea familiar to all. Suppose a visitor from outer space wanted to find the location of a particular street, say Bond Street in London. The visitor might go to a world atlas and determine first where London's country, England, is situated. The intergalactic traveler might then find a map of the country, and locate London. Finally, a city map of London gives the creature the exact location of the street. On a more mundane level, suppose a student wants to locate a particular book in the university library. The student would go to the file cabinet of authors and find the drawer that contains authors' last names with the appropriate beginning initial. She would then search for the card with the correct author and title, which gives a library call number. Next she would consult a library directory to learn the floor location of those call numbers. Finally, she would go to that location and search for the book with that particular call number. The critical concept in such searches is the availability of one or more directories, to be used to determine quickly the location of the particular item desired.
The magnetic disk supports the use of such a directory to focus the search. It can be used to find a particular cylinder and surface relatively quickly, eliminating the need for traversing sequentially through intervening records. Until recently, when B-trees (see next section) were introduced, the most popular method of creating and maintaining such a directory used the natural sequential storage of records, so that they appear in sorted order by key value. This is known as the indexed sequential access method (ISAM); it may be implemented in various ways, typically using three or four levels of directories. A first directory, known as the master index, may be searched to determine the cylinder on which a particular search key appears. If a disk pack has two hundred cylinders (tracks), then the master index has two hundred entries, one for each cylinder. The entry for the ith track gives the highest key value appearing on that track. A search of the master index then readily determines the cylinder on which a search key may reside. That cylinder is accessed; it contains a cylinder index directory. If a disk pack has ten surfaces, the cylinder index has ten entries, one for each surface. The entry for the ith surface gives the highest key value appearing on that surface. A search of the cylinder index determines the surface on which a search key may reside. Finally, the track of the cylinder on that surface may be searched sequentially for the desired key, resulting in a successful or unsuccessful search. With such an implementation, unused storage is initially left in blocks so that the insertion of new records may be more easily accommodated. If a block is full, records can be shifted to the right to other blocks, so that the new record is inserted in proper order.
Overflow areas must also be available and maintained on disk, in case the track storage is exhausted due to insertions. Tracks and cylinders are set aside for this purpose. Insertions may require the master or cylinder index to be updated. Similarly, deletions of records, leaving vacated storage to be reclaimed, may require updating of directories and shifting of records. Deletions may also be treated simply by marking a record as deleted, but this may eventually lead to the need for reclamation of this storage, degrading the efficiency of the implementation. Because of overflow from insertions, performance may degrade, necessitating reorganization, allocation of more disk storage, and reconstitution of the file.
The overflow areas may be maintained as lists of records in sorted order, linked by pointers. When the proper cylinder index is searched, the pointer to be followed may point to an overflow area, in which case the search amounts to a traversal of a list of records. Otherwise, the record is said to reside in the prime area, and the search amounts to a sequential traversal of records on a track. The prime area consists of reserved tracks on cylinders designated as prime cylinders.
For a given number of records to be stored, there is no guarantee that overflow will not degrade the system, unless a high price is paid by dedicating large amounts of track storage to reduce this possibility.
Each cylinder index actually has additional entries giving the highest key value in its overflow area for each surface and a pointer to the first record of the overflow list for the surface. Conceptually, we may visualize the organization of such implementations as shown in Figure 10.10.
A more recent method allows for achieving both the random access of records and a traversal through the records in sorted order. This method allows a more flexible use of the disk and guarantees excellent worst-case performance for a given number of records, with an acceptable amount of dedicated disk storage. It is known as the virtual sequential access method (VSAM). To see how it might be implemented, we study its basis B-trees. VSAM and many data base management systems use modified B-trees in their implementation. The basic reference for B-trees is the classic paper by Bayer and McCreight [1972]. Hash trees are an alternative to B-trees for the organization of large files of data. They are discussed and compared to B-trees by Bell and Deen [1984]. Tremblay and Sorenson [1984] discuss many file structure organizations. See Ullman [1982] for more on data base systems.
Figure 10.10 shows that the directories (the master index and the cylinder indexes) form a tree structure that guides the search for a record. Programmers try to find specialized trees leading to efficient searches, efficient use of storage, and relatively easy maintenance. Since the depth of the tree determines the worst-case search times, the goal is to find trees with short paths to terminal nodes. This implies that the nodes of the tree generally will have many successors. B-trees satisfy these requirements.
A B-tree of order m has the following four properties:
1. Every node of the tree, except the root and terminal nodes, has at least
2. Every terminal node has the same depth.
3. The root node has at least two subtrees, unless it is a terminal node.
4. No node has more than m subtrees.
Each node of a B-tree will have the form shown in Figure 10.11. This represents storage for m - 1 keys and m pointers, although the storage may not all be used at a given time. If n is less than m, not all m keys are present in the node. Each pointer Pi points to a subtree of the node. The keys K1, K2, . . . , Kn are kept in sorted order, so K1 < K2 <
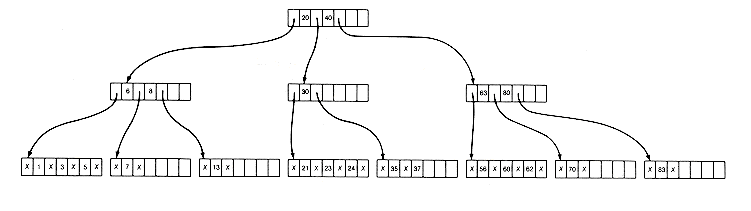
then the tree of Figure 10.12(a) is a B-tree of order 4 storing these keys and their records.
The terminal nodes of the B-tree in Figure 10.12 are not shown. Instead, the pointers to them have been replaced by null pointers. This reflects the way the tree might be represented in external storage. Notice that, in general, null pointers will appear at the same depth in the tree--depth one less than the terminal nodes. A generalized inorder traversal (see Chapter 7) of the B-tree accesses the keys in sorted order. Associate with each null pointer the key value accessed immediately after the pointer is considered in such a traversal. A unique key is then associated with every null pointer except the last, and each key has a unique null pointer associated with it. For example, the first three null pointers have keys 1, 3, and 5 associated with them. The fourth null pointer (to the right of 5) has key 6 associated with it. Consequently, the number of null pointers, and the number of terminal nodes, is exactly one greater than the number of keys stored in the tree.
Any B-tree has a root node with at least two successors. Each successor has at least
This implies that d < 2 + lgx
A B-tree storing 16,777,215 records will therefore have depth
A B-tree may be viewed as a generalization of a binary search tree, with a special imposed balance requirement to ensure against too great a depth. To search a B-tree for a search key value (say, 22) entails accessing its root node and traversing the node's keys until 22 is encountered, a key that exceeds 22 is reached, or the last key stored in the node is passed. If 22 is found, the search is complete. In Figure 10.12(a) the key value 40 is reached. The pointer to its left points to a subtree that must contain the search key, if it is in the tree at all. That subtree is then searched in the same way. Its root node is accessed, and 30 is reached. Following its left pointer, the final subtree root is accessed. Its key value, 23, is reached. Its left pointer is null, which means that the search terminates unsuccessfully.
Property 1 ensures that, except for the root and terminal nodes (which don't appear anyway), every node of a B-tree will be at least half full. Property 2 ensures that the B-tree will not be scraggly. All paths to terminal nodes must have the same length. The idea is to store information of a node on blocks of a cylinder on the disk, so that accessing a node requires one seek time and all keys of the node may be read into internal memory. The search through the keys of a node, to determine the next node to access, then takes place rapidly in internal memory, using an appropriate search technique.
After an insertion or deletion, of course, the tree must be maintained as a B-tree. This may be done making local modifications that are simpler than those required for AVL trees. For insertion, the key to be inserted is searched until a null pointer is to be followed. This assumes that only one record with a given key value appears in the tree and that it is similar to the initial insertion in AVL trees. If the node containing the null pointer has unused storage, then the key is simply inserted at the proper place in this node. This may require the shifting of keys in the node, but it is accomplished quickly in internal memory. For example, if key 35 is inserted in the tree of Figure 10.12(a), the result is the tree of Figure 10.12(b).
All insertions will be made in this way, in nodes at the lowest level, until the node becomes full. For example, if 28 is to be inserted next in the tree of Figure 10.12(b), no room exists in the node x 21 x 23 x 24 x . The m + 1 key values (the m old keys and the 1 new key) can be split by leaving
Had the predecessor been full, it would have been split in the same way in turn. Splitting may be necessary at every node of the search path, back to and including the root. If this occurs, the depth of the resultant B-tree is one greater than the original B-tree.
Deletion is done similarly. A key is simply deleted from a lowest-level node, and the keys shifted over, if the resultant number of keys satisfies the constraint that the node contain at least
If no neighbor can spare a key, the total number of keys between a neighbor and the deletion node will be less than m. These nodes may then be merged, along with a key from their predecessor. In the tree of Figure 10.12(d), if 83 is to be deleted, this situation will occur. The result is Figure 10.12(e).
It is possible for the predecessor to become too sparse, although this did not happen in our example. It is then treated as though its key were deleted, and so on, until the entire process is complete. This may go all the way to the root, in which case the root disappears and the depth of the tree decreases by 1.
If the key to be deleted were not in a lowest-level node, it would be replaced by its successor and the successor node treated as if the successor were being deleted.
These insertion and deletion procedures preserve the B-tree properties. The B-tree is an external memory data structure that plays the same role as AVL trees in internal memory. In practice, a modification of the basic B-tree is used to ensure better storage utilization and to increase the efficiency of traversal through the records in sorted order for VSAM. With B-trees the generalized inorder traversal must be used for sequential access. This is time-consuming and requires stack storage. Instead of storing some key records in higher-level nodes, the idea is to store all records only in lowest-level nodes and chain the lowest-level nodes by pointers. For example, in Figure 10.12(a) all nodes at depth 3 could be linked in a chain, with the leftmost node first and the rightmost node last on the list. A traversal then amounts to a traversal of this chain.
It is clear that storage management is needed for external memory, just as for internal memory. This problem is not discussed here, but the internal memory techniques are applicable, when properly modified to take into account the structure of the disks.
Files are stored in secondary storage and provide powerful facilities for the temporary and permanent storage of large amounts of data. Magnetic tapes and magnetic disks are two important devices on which to store files. These are typical of sequential and direct access devices, respectively.
Because of the structure and resultant access capabilities of these devices, internal memory techniques must be modified in order to deal efficiently and conveniently with files stored on them. It is possible to sort efficiently, even with sequential files, by using external sorting techniques. Primarily, these are merge sorts, such as straight, natural, and polyphase sorts. Other merge sorts may also decrease sorting time. In general, sequential files are suitable for tasks that can be accomplished by traversing the records of the file. These tasks include sorting and updating master files.
It is possible to achieve efficient random accessing of records with direct access devices when access is by a specific key. Hash tables are useful for this purpose. To achieve a combined capability of random plus sequential access in sorted order by a specific key requires considerable file organization. This organization involves the creation of a file directory, which may consist of a number of levels. The directory guides the search efficiently to the desired record with specific key value. A number of directory implementations are possible; directories based on B-trees are becoming increasingly popular. Such directories may be searched relatively quickly, allowing efficient insertions and deletions while utilizing storage well.
At this point, you should have filed away the substance of this book. It is hoped that you have done so to allow quick retrieval, while maintaining room for insertions. Deletions may be necessary but should be minimal.
1. Suppose a function reads in each record of Example 10.4 and creates a file consisting of every other prime number on the file. Show the state of the input and output files and their file pointers after the fourth record of the output file has been written.
2. Write a function to create the output file of Exercise 1.
3. Write a function to create reversedprime of Example 10.4, assuming the array a may only be of length 10 while reversedprime may contain many more entries.
4. How many writes and reads will be executed by the function merge if file 1 and file 2 are, respectively,
5. Write a function to create a sequential file that is the same as file 1, except that all records on file 1 that are also on file 2 do not appear.
a. Assume file 1 and file 2 records appear in sorted order based on the key field.
b. Assume file 1 and file 2 are not sorted, and you do not know how to sort a file.
6. Write a function to produce a new file that is the same as an input file except that all blanks have been deleted from it.
7. Write a function that takes two sequential files and appends the second file to the first.
8. Why are the sort procedures of Chapter 8 inappropriate for files?
9. Why does the number of passes required by a straight sort not depend on any initial ordering among records?
10. Write a function for the straight merge.
11. Modify the merge function of Section 10.3 so that it merges two runs embedded in files.
12. Write a function to distribute records as required by the natural merge.
13. Write a function for the natural merge.
14. Simulate the behavior of replacement-selection to verify that the average length run produced is 2m.
15. Why must Fibbonacci numbers govern the number of initial runs for three tapes in the polyphase sort?
16. a. If four tapes are used in a polyphase sort, what is the relation determining the initial distribution of runs?
b. Can you generalize to n tapes?
17. Write a function for the polyphase sort using three tapes.
18. Why do the movable read/write heads and surfaces act as tabs for a disk?
19. Suppose the master index of Section 10.7.3 does not fit on one cylinder. How may another directory level be created to serve as an index to the master index?
20. Why do B-trees allow more flexible use of a disk than directories implemented using prime and overflow areas?
21. Create a B-tree of order 4 to store the nametable records of Chapter 6. The records are to be ordered alphabetically so that the B-tree can be searched with the name field as key.
22. Write a function to insert a record into a B-tree of order m that is stored in internal memory.
23. Can you write the function of Exercise 22 so that it is independent of whether the B-tree is stored in internal or external memory? If so, write it. If not, explain why not.
24. Write a function to delete a record from a B-tree of order m that is stored in internal memory.
25. Why does the chaining of lowest-level nodes discussed in Section 10.7.4 allow more efficient traversal through a file?
26. Write a function to create a B-tree stored in internal memory.
27. Suppose we want to store variable length records in a B-tree. How may this be done?
28. Why is it not feasible to store all records in the root node of a B-tree so that only one seek is required?
29. A B-tree of order 3 is called a 2-3 tree, since each node has two or three successors.Although not useful for external storage, such a tree may rival AVL trees for an internal memory structure in which to store records. Compare its search, insertion, and deletion algorithms and its time requirements with those for AVL trees.
30. Write a search function for a B-tree of order m.
31. Write a function to traverse through the records of a B-tree in order by key value.
32. Suppose the individual records of Figure 6.5 are to be stored on a disk with the recordptr field of the nametable pointing to the address of an individual record on the disk. The address is a cylinder and surface specification. What is a reasonable way to allocate disk storage to the individual records?
33. Suppose records of a file were stored in a hash table, with buckets for random access by key, and linked in sequential order by pointers for sequential access. Compare the insertion and retrieval times of such an implementation with the use of B-trees.
This assignment is appropriate for a group of students to do together. It involves a task of reasonable size, which must be partitioned so that each member of the group knows just what to do and so that, when all parts are put together, the final solution works correctly. The idea is to produce an "index" for a book. This involves
1. The creation of files, using the sequential files available in C.
2. The creation of appropriate functions that will allow the records of a file to be accessed randomly, or in sequential order, by key.
One file, the book file, is to consist of records that represent the pages of a book. Each page contains one hundred lines, and each line consists of one hundred characters. The key consists of a page number and a line number. A second file, the dictionary file, is to consist of records representing words to appear in an index for the book represented on the book file. When the solution is run, it should use a scaled-down version of the book file, which will consist of a few pages of ten lines and twenty characters each, with the dictionary containing relatively few words (say, twenty-five).
The dictionary file is to be a sequential file, with the file implemented using B-trees. Instead of a disk, assume that enough internal memory exists to store the book file. The index for the book should be output so that the words of the index appear in alphabetical order, followed by the page and line numbers on which the word appears in the book. Also, an input file consisting of page and line numbers appearing in random order should result in an output consisting of the text for each record of this input file.
10.2.1 Operating Systems
10.2.2 Filters
10.3: Organization of Files
10.3.1 Sequential Files
typedef struct
{char title[MAXTITLE];
char author[MAXAUTHOR];
char publisher[MAXPUBLISHER];
float price;
int currentstock;
}bookrecords;
bookrecords bookinventory;
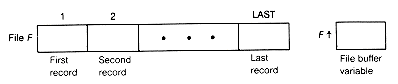
Figure 10.1 File F and F

FILE *f_ptr;
f_ptr = fopen("bookinventory", "r");if(f_ptr == NULL)
printf("Can not open the file");fread( pointer to the location of the , size of , number of, pointer to )
memory in which the records record to records to the file to
read are to be placed be read be read be read
fread(&bookinventory,sizeof(bookrecords),1,f_ptr);
fwrite(&bookinventory,sizeof(bookrecords),1,f_ptr);
#define NULL 0
#include <stdio>
main()
/* Creates a file consisting of the first 10 prime
numbers, and a file containing these primes in
reversed order, and prints the contents of both
the files.
*/
{/* This section creates file prime and
stores the first ten primes in it.
*/
int a[20],i,dummy;
FILE *f_ptr,*fr_ptr,*fopen();
f_ptr = fopen("prime","w");fprintf(f_ptr,"%d",2);
fprintf(f_ptr,"%d",3);
fprintf(f_ptr,"%d",5);
fprintf(f_ptr,"%d",7);
fprintf(f_ptr,"%d",11);
fprintf(f_ptr,\"%d\",13);
fprintf(f_ptr,"%d",17);
fprintf(f_ptr,"%d",19);
fprintf(f_ptr,"%d",23);
fprintf(f_ptr,"%d",29);
fclose(f_ptr);
/* This section reads from the prime file,
fills a with its contents, and creates
reversedprime which will contain
the contents of a in reversed order.
*/
i = 0;
(1) f_ptr = fopen("prime","r");if(f_ptr == NULL)
{printf("Can not open");exit(-1);
}
while(fscanf(f_ptr,"%d",&dummy) != EOF)
{a[i] = dummy;
i++;
}
i--;
(2) fr_ptr = fopen("reversedprime","w");if(fr_ptr == NULL)
{printf("Can not open");exit(-1);
}
while(i >= 0)
{fprintf(fr_ptr,"%d",a[i]);
i--;
}
fclose(f_ptr);
fclose(fr_ptr);
/* This section prints, at the terminal,
the contents of prime and then of
reversedprime.
*/
f_ptr = fopen("prime","r");while(fscanf(f_ptr,"%d",&dummy) != EOF)
printf("\n %d\n",dummy);fr_ptr = fopen("reversedprime","r");while(fscanf(fr_ptr,"%d",&dummy) != EOF)
printf("\n %d\n",dummy);fclose(f_ptr);
fclose(fr_ptr);
}
f_ptr = fopen("prime","a");fprintf(f_ptr,"%d",31);
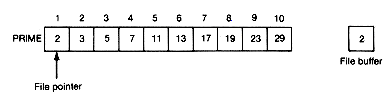
(a) After FOPEN Is Executed

(b) After Nine Executions of the While Loop
Figure 10.2 File PRIME

(a) After FOPEN Is Executed

(b) After Nine Executions of the Second While Loop

(c) After Last Execution
Figure 10.3 File REVERSEDPRIME
merge(f1_ptr,f2_ptr,f3_prt)
/* Merges the files pointed to by f1_ptr
and f2_ptr. The merged file is pointed
to by f3_prt. The files must be opened before the merge is invoked.
*/
FILE *f1_ptr,*f2_ptr,*f3_ptr;
{struct filerecords record1,record2;
int flag,length;
flag = 0;
length = sizeof(filerecords);
fread(&record1,length,1,f1_ptr);
fread(&record2,length,1,f2_ptr);
while(flag == 0)
if(record1.key < record2.key
{fwrite(&record1,length,1,f3_ptr);
if(fread(&record1,length,1,f1_ptr) == 0)
{flag = 1;
fwrite(&record2,1ength,1,f3_ptr);
}
}
else
{fwrite(&record2,length,1,f3_ptr);
if(fread(&record2,length,1,f2_ptr) == 0)
{flag = 2;
fwrite (&record1,length,1,f3_ptr);
}
}
if(flag == 1)
while(fread(&record2,length,1,f2_ptr) != 0)
fwrite(&record2,length,1,f3_ptr);
else
while(fread(&record1,1ength,1,f1_ptr) != 0)
fwrite(&record1,1ength,1,f3_ptr);
}
#define NULL 0
#include <stdio>
typedef struct
{int key;
}filerecords;
main()
/* Merges two files and prints the merged file.
*/
{filerecords record;
FILE *f1_ptr,*f2_ptr,*f3_ptr;
f1_ptr = fopen("prime","r");if(f1_ptr == NULL)
{printf("Can not open file1");exit(-1);
}
f2_ptr = fopen("other","r");if(f2_ptr == NULL)
{printf("Can not open file2");exit(-1);
}
f3_ptr = fopen("result","w");if(f3_ptr == NULL)
{printf("Can not open file3");exit(-1);
}
merge(f1_ptr,f2_ptr,f3_ptr);
fclose(f1_ptr);
fclose(f2_ptr);
fclose(f3_ptr);
f3_ptr = fopen("result","r");while(fread(&record,sizeof(filerecords),1,f3_ptr) != 0)
printf("\n %d\n",record.key);fclose(f3_ptr);
}
10.4: Sequential Access in External Memory

Figure 10.4 Sequential Access on Magnetic Tape
Figure 10.5 Input Buffer for the File
10.5: Sorting Tape Files
2 12 17 16 14 30 17 2 50 65 20 32 48 58 16 20 15 10 30 45 16
10.5.1 Straight Merge
a 2|17|14|17|50|20|48|16|15|30|16
b 12|16|30| 2|65|32|58|20|10|45|
2 17 14
12 16 30, etc.
c 2 12|16 17|14 30|2 17|50 65|20 32|48 58|16 20|10 15|30 45|16
a 2 12|14 30|50 65|48 58|10 15|16
b 16 17| 2 17|20 32|16 20|30 45|
c 2 12 16 17|2 14 17 30|20 32 50 65|16 20 48 58|10 15 30 45|16
a 2 12 16 17|20 32 50 65|10 15 30 45
b 2 14 17 30|16 20 48 58|16
c 2 2 12 14 16 17 17 30|16 20 20 32 48 50 58 65|10 15 16 30 45
a 2 2 12 14 16 17 17 30|10 15 16 30 45
b 16 20 20 32 48 50 58 65|
c 2 2 12 14 16 16 17 17 20 20 30 32 48 50 58 65|10 15 16 30 45
a 2 2 12 14 16 16 17 17 20 20 30 32 48 50 58 65
b 10 15 16 30 45
c 2 2 10 12 14 15 16 16 16 17 17 20 20 30 32 45 48 50 58 65
10.5.2 Natural Merge
a 2 12 17|14 30
b 16
a 2 12 17|14 30
b 16 17
a 2 12 17|14 30 |20 32 48 58|15 16
b 16 17 | 2 50 65|16 20 |10 30 45
c 2 12 16 17 17|2 14 30 50 65|16 20 20 32 48 58|10 15 16 30 45
a 2 12 16 17 17|16 20 20 32 48 48
b 2 14 30 50 65|10 15 16 30 45
c 2 2 12 14 16 17 17 30 50 65|10 15 16 16 20 20 30 32 45 48 58
a 2 2 12 14 16 17 17 30 50 65
b 10 15 16 16 20 20 30 32 45 48 58
c 2 2 10 12 14 15 16 16 16 17 17 20 20 30 30 32 45 48 50 58 65
10.5.3 Replacement-Selection
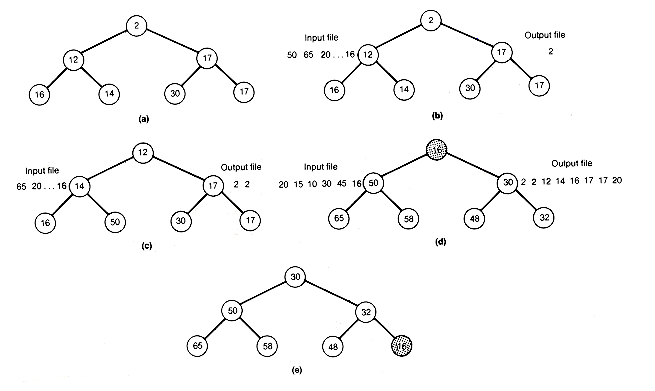
Figure 10.6 Replacement-Selection Sort
2 2 12 14 16 17 17 20 30 32 48 50 58 65|10 15 16 16 20 30 45
10.5.4 Polyphase Sort
a 2
 12
12 17
17 16
16 14
14 30
30 17
17 2
2 50
50 65
65 20
20 32
32 48 13 runs of length 1
48 13 runs of length 1b 58
 16
16 20
20 15
15 10
10 30
30 45
45 16
16 8 runs of length 1
8 runs of length 1c
a 50
 65
65 20
20 32
32 48 5 runs
48 5 runsb
c 2 58
 12 16
12 16 17 20
17 20 15 16
15 16 10 14
10 14 30 30
30 30 17 45
17 45 2 16 8 runs
2 16 8 runsa
b 2 50 58
 12 16 65
12 16 65 17 20 20
17 20 20 15 16 32
15 16 32 10 14 48 5 runs
10 14 48 5 runsc 30 30
 17 45
17 45  2 16
2 16  3 runs
3 runsa 2 30 50 58
 12 16 17 45 65
12 16 17 45 65 2 16 17 20 20 3 runs
2 16 17 20 20 3 runsb 15 16 32
 10 14 48 2 runs
10 14 48 2 runsc
a 2 16 17 20 20 1 run
b
c 2 15 16 30 30 32 50 58
 10 12 14 16 17 45 48 65 2 runs
10 12 14 16 17 45 48 65 2 runsa
b 2 2 15 16 16 17 20 20 30 30 32 50 58 1 run
c 10 12 14 16 17 45 48 65 1 run
a 2 2 10 12 14 15 16 16 16 17 17 20 20 30 30 32 45 48 50 58 65
b
c
10.6: Direct Access in External Memory
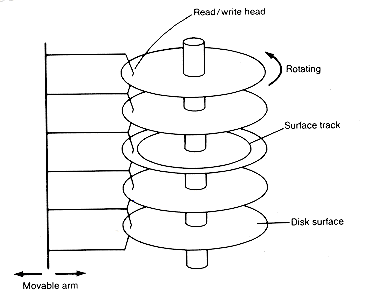
Figure 10.7 A Disk Pack
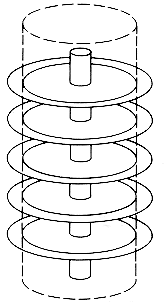
Figure 10.8 Conceptual Cylinder
10.7: Sequential and Random Access of Disk Files
10.7.1 Sequential Access

Figure 10.9 Sequential Access on a Magnetic Disk Pack
 c seeks, where c is a small constant.
c seeks, where c is a small constant.10.7.2 Random Access
10.7.3 Indexed Sequential Access
10.7.4 B-trees for Sequential and Random Access
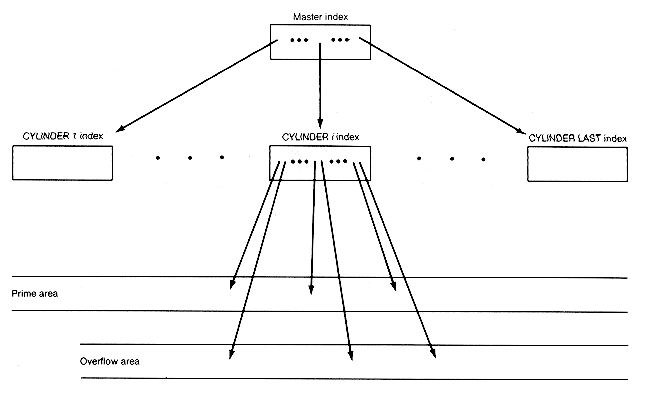
Figure 10.10 Organization of Indexed Sequential Files
 1/2 m
1/2 m subtrees.
subtrees.

 < Kn within the node. The subtree pointed to by Pi+1 contains all records of the file whose key values are less than Ki+1 and greater than or equal to Ki. P1 and Pn+1 point to subtrees containing records with key values less than K1 and greater than or equal to Kn, respectively. For example, if the keys are
< Kn within the node. The subtree pointed to by Pi+1 contains all records of the file whose key values are less than Ki+1 and greater than or equal to Ki. P1 and Pn+1 point to subtrees containing records with key values less than K1 and greater than or equal to Kn, respectively. For example, if the keys are1,3,5,6,7,8,13,20,21,23,24,30,37,40,56,60,62,63,70,80,83
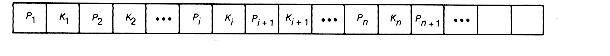
Figure 10.11 Form of Each Node on a B-Tree
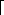 1/2 m
1/2 m successors. Thus there are at least 2
successors. Thus there are at least 2 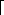 1/2 m
1/2 m d-2 nodes at depth d > 3 of any B-tree. A B-tree of depth d > 3 has at least 2
d-2 nodes at depth d > 3 of any B-tree. A B-tree of depth d > 3 has at least 2 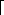 1/2 m
1/2 m d-2 terminal nodes, so
d-2 terminal nodes, son + 1 > 2
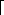 1/2 m
1/2 m d-2
d-2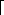 (n + 1)/2
(n + 1)/2 , where lgx denotes logarithm with base x and x =
, where lgx denotes logarithm with base x and x = 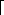 1/2 m
1/2 m . If n = 224 - 1 = 16,777,215 and m = 2 X 28 = 512, then (n + 1)/2 = 223, and lgx [(n + 1)/2] = lg256(223) < 3.
. If n = 224 - 1 = 16,777,215 and m = 2 X 28 = 512, then (n + 1)/2 = 223, and lgx [(n + 1)/2] = lg256(223) < 3. 4. We shall see that d - 1 is the maximum number of nodes that must be accessed when searching a B-tree for a search key. Thus we are guaranteed that no more than three node accesses are required to search for a key in the B-tree with 16,777,215 records!
4. We shall see that d - 1 is the maximum number of nodes that must be accessed when searching a B-tree for a search key. Thus we are guaranteed that no more than three node accesses are required to search for a key in the B-tree with 16,777,215 records!
(a) Initial B-tree
(b) After Insertion of 35
Figure 10.12 A B-Tree of Order 4 with Twenty-one Records
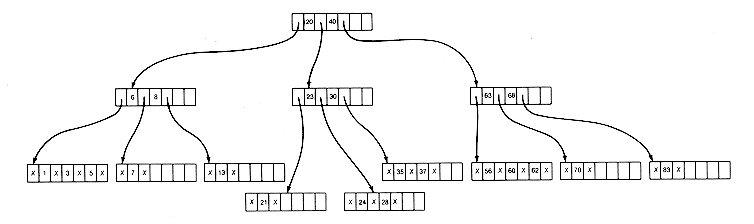
(c) After Splitting, Due to Insertion of 28
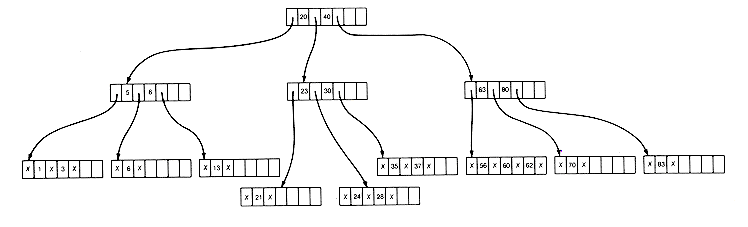
(d) After 7 is Deleted and 5 is Borrowed
Figure 10.12
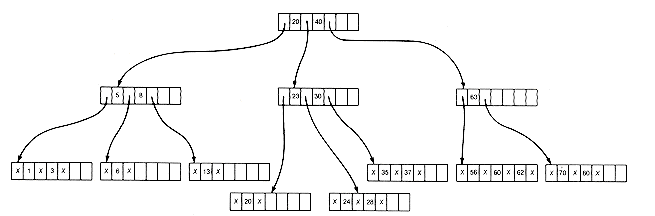
(e) After Deletion of 83 and Merging
Figure 10.12
 m/2
m/2 - 1 in the old node and moving the remaining records, except the middle one, the
- 1 in the old node and moving the remaining records, except the middle one, the 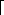 1/2m
1/2m th, to a newly created node. The middle record is inserted in the predecessor (parent) of the old node. The result is the B-tree of Figure 10.12(c).
th, to a newly created node. The middle record is inserted in the predecessor (parent) of the old node. The result is the B-tree of Figure 10.12(c).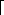 m/2
m/2 - 1 keys. If the constraint is violated, a key can be borrowed from a "neighbor" node, provided this may be done without violating the constraint for that node. In this case, the predecessor or successor key of the borrowed key moves into the deletion node, and the borrowed key takes its place in the predecessor node. For example, if key 7 is deleted from the tree of Figure 10.12(b), key 5 is borrowed from its neighbor (13 cannot be borrowed). The result is Figure 10.12(d).
- 1 keys. If the constraint is violated, a key can be borrowed from a "neighbor" node, provided this may be done without violating the constraint for that node. In this case, the predecessor or successor key of the borrowed key moves into the deletion node, and the borrowed key takes its place in the predecessor node. For example, if key 7 is deleted from the tree of Figure 10.12(b), key 5 is borrowed from its neighbor (13 cannot be borrowed). The result is Figure 10.12(d).10.8: Summary
Exercises
1 2 8 10 13 15 40
3 7 10 12 17 20 45 50 60
Suggested Assignment


