Topological sorting requires ranking a set of objects subject to constraints on the resultant topology--that is, on the placement of the objects. It occurs in many practical situations. For example, textbooks are often written so that each chapter builds on material covered earlier and cannot be understood without this base of information. Determining the order in which to present topics to ensure that all prerequisite material has been covered reduces to finding a topological sort of the topics. Other examples involving topological sorting are presented later.
The approach to the topological sorting problem presented in this chapter and the characteristics of the final program are intended to serve as prototypes. The problem is substantial and the algorithm developed important, but it is the process by which it is achieved that is most important. Developing an efficient topological sorting program is a complex process and demonstrates the general problem solving methodology used in this text. It requires the application of structured programming concepts, during which the selection of data structures plays a significant role.
The resultant topological sorting program is a model solution, representing nearly the best programmers can hope to achieve. Few solutions to problems have all its characteristics. It is concise and clear; correctness is easy to determine; and the storage and execution time requirements can be analyzed. Invalid input data are not difficult to deal with. What more can we ask?
The following are some examples of problems whose solutions require topological sorting.
Example 11.1
A large skyscraper is to be constructed. Imagine that you must write a program to prescribe the order in which all the tasks are to be performed. The tasks include T3--install windows; T50--install floors; T8--install window sashes; T1000--clear the ground; T7--build the foundation; T9--install doors. For any two tasks, it is possible to specify whether one should be done before the other. Clearly, T8 must be done before T3, and T1000 must be done before T7, while it makes no difference whether or not T3 is done before T9. The constraint that Ti be done before Tj is represented as the pair (i, j).
Example 11.2
Imagine that you want to write a book on data structures. All technical words used must be defined. First write down all the relevant words. If word wj uses wi in its definition, represent this constraint by the pair (i, j).
Example 11.3
As a student you must take a number of courses to graduate. Represent the fact that course cj has course ci as a prerequisite by the pair (i, j).
Example 11.4
A number of books must be read for a course you are taking. Represent the fact that you prefer to read book i before book j by the pair (i, j).
Suppose that an order is given in which the construction tasks of Example 11.1 are to be carried out. If you proceed to carry out the tasks, you may not be able to do the next task, since tasks that must precede it have not yet been finished. The same situation can arise in Examples 11.2, 11.3, and 11.4, when an order is specified in which words are to be defined, courses to be taken, and books to be read, respectively. This is because words used in the next word's definition have not yet been defined, all prerequisites for the next course may not have been taken, or you will not read the next available book because you want to honor your preferences. A topological sort gives an order in which to proceed so that such difficulties will never be encountered.
Some mathematical concepts and terminology must be defined before the topological sorting problem can be stated and solved in abstract terms. As with the solution to any problem, stating this solution abstractly is desirable so that it will not be tied to a particular application.
You readily understand what is meant by the statements: "Fred is related to Sam"; "John is taller than Sue"; "3 is the square root of 9." The phrases each specify a connection or relation between two objects. In the first two cases the relations refer to two people. In the third case the relation refers to numbers. Each is a binary relation on a set of objects.
Mathematics abstracts from such examples to define a binary relation R on a set S. S is taken as the set or collection of objects referred to by the relation. R contains information, for any two of these objects, on whether or not they are related. R is a set of pairs of objects (a, b), where a and b belong to S. If the pair (a, b) belongs to R, then this is interpreted to mean that a is related to b. This is written as aRb. If (a, b) does not belong to R, then a is not related to b. This is written as
For instance, specify S to be the set of integers between 2 and 10, so S = {2, 3, . . . , 10}; and take R = {(4, 2), (6, 2), (8, 2), (8, 4), (9, 3), (10, 2), (6, 3), (10, 5)}.Then R captures the "is divided evenly by but is not equal to" relation on S, since a pair (a, b) will belong to R only if a "is divided evenly by but is not equal to" b. By looking at R, we can determine if aRb or
Of particular interest are the kinds of binary relations called partial orders. A binary relation R on S is called a partial order on S if it has the following properties:
Irreflexivity For any a in S,
Asymmetry For any two distinct a and b in S, aRb implies
Transitivity For any three distinct a, b, and c in S, aRb and bRc implies aRc
These properties specify that whenever certain pairs are in R, then other pairs must necessarily be included in R or excluded from R. The "is divided evenly by but is not equal to" relation on S in the preceding paragraph fulfills all three properties of a partial order.
It is irreflexive, since a is divided evenly by but is equal to a for all a in S.
It is asymmetric, since if a "is divided evenly by" b, then b cannot be divided evenly by a when a is not equal to b.
It is transitive, since whenever a is divided evenly by b and b is divided evenly by c, then a must also be divided evenly by c.
To show that a relation does not have a property requires only one counter-example.
Two extreme binary relations on a set S are the null relation, which contains no pairs at all, and the universal relation, which contains all possible pairs. The null relation is a partial order. This is because no counterexamples can be found. The universal relation will never be irreflexive (unless S has no objects in it) or asymmetric (unless S has only one object), but it will always be transitive.
One can represent any binary relation R on a set of n objects graphically, as in Figure 11.1. Let S consist of ten objects, the integers 1, 2, 3, . . . , 10. Take R to contain the pairs (1, 2), (8, 3), (7, 6), (2, 7), (5, 4), (7, 8), (2, 4), (4, 7), (2, 8), (8, 5). Create a node for each object in S and draw arrows between two nodes for each pair in R. For example, an arrow will appear from 7 to 8 for the pair (7, 8).
Any such diagram can be interpreted as representing a binary relation on a set S. For such a diagram to represent a partial order requires that
No arrows appear from any node to itself (irreflexivity)
No arrows appear from any node i to another node j and back from j to i (asymmetry)
If arrows appear from i to j and from j to k, then an arrow must appear from i to k (transitivity)
In depicting partial orders, it is unnecessary to draw all the arrows needed to represent transitivity, because they are always assumed. With this understanding, it is not difficult to see that a diagram represents a partial order if and only if it contains no loops. This means that no node can be found such that one can follow a series of arrows starting from that node and ending at that node. In Figure 11.1, there is a loop involving nodes 5, 4, 7, and 8. Hence the diagram does not represent a partial order. Note that if one starts with a diagram representing a partial order (no loops), erasing a node and all arrows emanating from it results in a diagram that represents a new partial order on the set of remaining nodes.
Partial orders are important. They are meant to capture abstractly any concrete example in which the pairs of R (or arrows of the diagram) mean "is greater than," "precedes," "is ranked higher than," or "comes before." A special case of a partial order is one whose diagram looks like the following:
For such a diagram, it seems clear what would be meant by a listing or ranking of the eight objects that is consistent with the given partial order. Such a ranking would be 3, 5, 1, 2, 4, 6, 8, 7. No other ranking would be consistent with the given partial order. This can be generalized to any partial order by interpreting the arrows as constraints on the ordering of objects in a ranking. For example, an arrow from 3 to 5 would mean that 3 must be ranked higher than 5. Then, a ranking consistent with a partial order would mean a ranking of the n objects that violates no constraints (that is, a ranking that violates no arrows or pairs).
Example 11.5
Consider the partial order on the set of nine integers represented by Figure 11.2.
The ranking 2, 3, 4, 5, 6, 7, 8, 9, 10 would not be consistent with this partial order, because it violates at least one of the constraints--namely, that 6 be ranked higher than 3, or that 10 be ranked higher than 2. This diagram actually represents the "is divided evenly by but is not equal to" relation introduced earlier.
The definition of topological sorting can now be stated more formally than at the outset of the chapter. A topological sort is a ranking of the n objects of S that is consistent with the given partial order. Let us try to solve the following topological sorting problem.
Example 11.6
Given a partial order on a set S of n objects, produce a topological sort of the n objects, if one exists. If no such ranking exists, then print out a message saying that none exists.*
* If a relation is asymmetric and transitive but not irreflexive, then one can eliminate all pairs of the form (x, x) from the relation or, equivalently, erase all self-loops from its diagram. The resulting relation is a partial order, and it still makes sense to find a topological sort with respect to it. The topological sort then satisfies the constraints of the original relation involving distinct objects.
For simplicity assume that S is always the set of the first n integers 1, 2, 3, . . . , n, and that the partial order is given as m pairs of integers representing arrows in the corresponding diagram. Assume no pairs are replicated. For concreteness, take the input to have the following form:
This particular instance of the topological sorting problem will be referred to repeatedly throughout the chapter. Is there an obvious algorithm for this problem? Try to think of one before continuing.
Consider the specific ranking 4, 8, 1, 2, 7, l0, 9, 5, 3, 6 of the 10 objects of the example. It is easy to determine whether or not this ranking violates any constraints of the partial order by checking each one. Since this ranking violates two of the nine constraints, 6
A search-based algorithm:
If a ranking is found which violates no constraints, then the ranking is a topological sort, print it and stop. If all possible rankings have been tried and no topological sort found, then print out the message that none exists, and stop.
To implement this algorithm in a programming language requires finding a way to generate the rankings so that all the distinct rankings are eventually generated. The procedure permutations of Chapter 4 does this. Any implementation of the algorithm could take time proportional at least to the number of distinct rankings of n objects. A particular ranking can be constructed by selecting any one of the n objects to be first in the ranking, then selecting any one of the remaining n - 1 objects to be second in the ranking, and so on. Thus there are n X (n - 1) X (n - 2) X
* See Section 1.8.2.
The first solution to Example 1l.6 searched through all possible rankings. Another approach is to attempt the construction of the required ranking. To this end consider a ranking, obj1, obj2, . . . , objn, of the n objects that is a topological sort with respect to a given diagram. What can be said about obj1, the highest-ranked object? Clearly there must be no objects that are constrained by the diagram to appear higher in the ranking than obj1. Otherwise, those constraints would be violated, and the ranking would not be a topological sort. In terms of the diagram, this means that no arrows must point to obj1. We describe this by saying that obj1 must have no predecessors.
Now suppose the node corresponding to obj1 is erased, as well as all the arrows emanating from obj1. As noted earlier, this results in a new diagram that represents a new partial order on the remaining n - 1 objects. Consider the ranking of these n - 1 objects obtained by taking the original topological sort of the n objects and removing obj1. That is, consider obj2, obj3, . . . , objn. It must be a topological sort of the remaining n - 1 objects in the new diagram with respect to the new partial order. This is because any constraint in the new diagram that is violated by this ranking would have been violated in the original ranking of the n objects. Note that if any topological sort of the remaining n - 1 objects were taken with respect to the new partial order, and obj1 were placed in front of it, the ranking of n objects thus obtained would be a topological sort with respect to the original partial order. Placing obj1 first in this ranking cannot violate any of the original constraints because they did not require that any object precede obj1.
We have just discovered how to construct a topological sort:
A construction-based algorithm:
While S is not empty
1. Select any object with no predecessors.
2. Place it in the next position of the output ranking.
3. Remove that object from S, and
4. Remove its arrows from the partial order.
The output ranking produced will always be a topological sort.
One difficulty remains. How can the programmer be certain the algorithm can actually be carried out? It may be impossible to carry out because at some point there may be no objects with zero predecessors. That this is indeed an algorithm requires showing that there always is at least one object with no predecessors.
One method of proof for any proposition is to assume it is not true and then show that this assumption leads to a contradiction. This method of proof is applied here. The goal is to prove that every time the loop task is to be carried out, at least one object with no predecessors can be found among those remaining. To assume that this is not true means that at some point the task cannot be carried out because every object left has at least one predecessor. Recall that the original diagram, representing a partial order, had no loops. It will be shown that the assumption implies a loop in the diagram. This will be the contradiction.
Suppose i1 is one of the remaining objects. Under the assumption, every object has at least one predecessor, so i1 has a predecessor (say, i2). Note that i2 cannot be the same object as i1, or the irreflexivity property would not hold. Again, i2 must have a predecessor (say, i3). The object i3 cannot be i1 or i2. If it were i1 or i2, then a loop involving i2 and i1 or a loop with just i2 would exist. Continuing with this argument, i1, i2, i3, i4, . . . must all be distinct objects. But since there are only n objects in total, eventually an object must repeat. This implies that the repeated object is the starting and ending object of a loop. The conclusion is that the assumption was false. Therefore what we wanted to prove must be true, and we never get bogged down--there will always be an object with no predecessors.
This algorithm yields additional insight into the topological sorting problem. Since it is clear that the loop can always be carried out to completion, it will always produce a topological sort of the n objects. In other words, a topological sort always exists. This was certainly not obvious before.
To be sure the algorithm is understood, it is applied next to Example 11.6, depicted again in Figure 11.3. Initially (see Figure 11.3(a)), 4, 7, 5, and 9 have zero predecessors.
The first step is to select and remove 5 (either 4, 7, or 9 could also have been removed) and its successor arrows, to obtain Figure 11.3(b). S is not empty, so the loop must be repeated. Now, 4, 7, and 9 have no predecessors. Select and remove 7 and its successor arrows, and obtain Figure 11.3(c). S is still not empty, and now 4, 9, 1, 3, and 6 have no predecessors. Select 4. Updating produces Figure 11.3(d).
S is still not empty, but 9, 1, 3, 6, and 2 now have zero predecessors. Continuing in this way, removing 1, 3, 6, 8, 9, 2, and finally 10 in succeeding iterations yields the final ranking: 5, 7, 4, 1, 3, 6, 8, 9, 2, 10.
Notice that every time an object is selected and removed, the diagram is updated to reflect the new S and the new partial order. As a result, some additional objects may end up with zero predecessors. Once an object has zero predecessors, it will remain in each succeeding diagram, always with zero predecessors, until it is removed.
The first refinement describes an implementation of the algorithm.
First refinement:
1. Read n.
2. Initialize for phase I.
3. While there is another input pair,
a. record the information in the pair i, j phase I
4. Initialize for phase II. phase II
5. While the set S is not empty,
a. select an object with no predecessors, and output it as the next object in the output ranking;
b. update the records to reflect the removal of the output objects.
Phase I reads into memory the information about the number of objects and the partial order. Every time an i, j pair is read in, the new information that this represents must be incorporated into a representation in memory. The "record the information" of task 3a refers to the modification of this representation to reflect the new arrow, i
Phase II describes the processing required by our algorithm. Task 5a involves the selection, removal, and outputting of an object. Task 5b involves modifying the partial order representation and S, to reflect the removal of an object and its arrows, and outputting it in the ranking. After task 5b is carried out, that representation should reflect the new set S and the new partial order resulting from the object's removal.
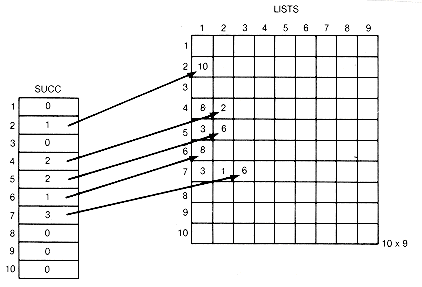
A straightforward representation of the partial order would be to keep an image in memory of all input arrows. We might use two arrays, first and second, for this purpose. First would contain the first integer, and second would contain the second integer of an input pair. The "record the information" task would then involve putting i and j into the next available locations of first and second, respectively. For Example 11.6, after phase I was executed, the result would be the arrays shown in Figure 11.4.
Suppose the while loop of phase II is being executed, and task 5a is to be carried out. An object with no predecessors must be selected. How is such an object found? Any object that has no predecessors will not appear in the second array. Somehow the second array must be searched to select an object with no predecessors. This can be accomplished by using an array S, traversing second, and marking location i of S when object i appears in second. Any location in S left unmarked corresponds to an object with no predecessors.
Suppose this is done, and object 5 is selected. Object 5 can then be output to the next place in the ranking. To accomplish task 5b, the "updating of the records," then requires that the array first be traversed. As it is traversed, each time a 5 is encountered, the program must mark the location of first in which it appears, and the corresponding location of second. The mark signifies that the corresponding arrow emanating from 5 has been removed from the representation.
This completes one execution of the loop. This same processing must be repeated for each repetition of that loop. The loop will be repeated n times, once for each of the n objects. The first and second arrays must be traversed each time. This will take time proportional to their length, which, in general, will be m. Hence this implementation of the algorithm will take time proportional to n X m. The storage required is roughly 2m locations for first and second, and n locations for S.
It is apparent that a lot of time is spent finding the information needed to carry out the processing in phase II. Efficiency can be improved by focusing on the following important question. Precisely what information is needed to carry out the processing?
Notice that each time through the loop, the program must select an object with no predecessors. To do this requires kdnowing which of the objects left in S have zero predecessors. Suppose that it is known, before and after each execution of the loop body, exactly how many predecessors each remaining object has. With this knowledge, an object with zero predecessor count can be selected. Once an object becomes eligible to be selected (has zero predecessors), it remains eligible until it is actually selected. Why not collect all those initially eligible in the initialization for phase II? The program could then select among them arbitrarily. Think of this collection as kept in a bag from which the object selected for output is pulled.
As the rest of the loop body is executed, the records must be updated to reflect the removal of this object and its arrows. Removing its arrows amounts to reducing the predecessor count of each successor of the object removed.Whenever the predecessor count of one of these successors becomes zero, that successor becomes eligible for selection on the next repetition of the loop. That successor is immediately added to the bag. Consequently, at the start of each loop repetition, the bag will contain exactly those objects eligible for selection, thus eliminating the need to search for them. In fact, the "S not empty" test is now equivalent to asking if the "bag is not empty." Keeping track of the successors of each object eliminates the need to search for them when that object is output. Incidently, we now know two operations that will be needed on the count collection, decrease(i,count) and iszero(i,count). The first reduces the count of the ith object by one, and the second returns true only if the count of the ith object is zero. The precise information needed for processing has now been isolated. What must be known are the predecessor counts and successors for each object, and what's in the bag.
The loop body of phase I must update predecessor counts and successors.The input pair i, j contains the information that j has one more predecessor than currently reflected in j's predecessor count, and that i has one more successor, j, than currently reflected by i's successors. The loop body of phase II must update the predecessor counts of all successors of the removed object. It must also update the bag. We have developed the following better refinement of the algorithm.
A better refinement:
1. Read n.
2. Initialize
a. Initialize the predecessor counts for each of the n objects to zero.
b. Initialize current successors for each of the n objects to zero.
3. While there is another input pair,
a. increase the predecessor count of j by l;
b. add j to the current successors of i.
4. Place all objects with zero predecessor count into the bag.
5. While the bag is not empty,
a. remove an object from the bag and output it in the output ranking;
b. for each successor of the output object, decrease its predecessor count by l; if the predecessor count becomes zero, add the successor to the bag.
The implementation treats the predecessor counts, the collections of successor counts, the bag, and the output ranking as data abstractions. In order to refine the solution further, we must decide how to store the predecessor counts, the successors of each object, the bag, and the output ranking. These are data structure decisions. They should be based on the kinds of operations to be performed in tasks 1 through 5. First we functionally modularize the solution.
1. read(n);
2. a. predinitialization(n,count);
b. succinitialization(n,successor);
3. while nextpair(i,j)
a. increase(j,count);
b. insert(i,j,successor)
4. baginitialization(bag,n,count);
5. while not emptybag(bag)
a. remove(bag,obj);
b. update(successor,obj,bag,count)
Every operation performed in tasks 1 through 5 that involves the bag, any of the n predecessor counts or collections of successors, or the output ranking has been implemented by a corresponding function. Note the use of a prefix to designate the structure involved in some of these operations. When written in this form, the program is independent of the specific details of implementation of each of these structures. This means that even if changes in the data structure implementations are ultimately adopted, this version of the solution will never need to be modified.
The next step is to decide on specific data structures for implementation of the data abstractions. This choice must be based on the functions that operate on the data structures. These functions include predinitialization,succinitialization, increase, decrease, iszero, insert, baginitialization, emptybag, and remove.
At some future time a decision may be made to change the implementation of any data abstraction. This requires finding all declarations and definitions of the data structures and functions involved and replacing them with the new versions.This modification may be made more easily and more reliably when the originals have been localized in the program. Such localization is called encapsulation. Not all high-level languages provide appropriate tools for achieving the same degree of encapsulation. In the ideal final program the data abstractions are defined in precisely one place; even more important, no operations are allowed on the corresponding data structures except those specified by the functions of the data abstraction. In the implementation above, this means, for example, that for the bag only the baginitialization, emptybag, remove, plus any other operations we take as basic to the bag will appear together. This makes it easier to determine which operations may be affected by a new implementation of the bag.The greater the encapsulation and modularization, the more expeditious the process of achieving correct modifications and adaptations. How to do this in C was discussed in Chapter 5.
We are actually in a position now to make a decision on the implementations for count, successor, and bag. The programmer does not know, in advance, the order in which objects will be output. In task 5b of the better refinement, after an object is output, its successors must be accessed and their predecessor counts updated. This means that the predecessor counts and the collections of successors must be accessed in arbitrary order. Because arrays support random access to their entries, we choose to store the predecessor counts in an array count and pointers to each collection of successors in an array succ. Count[i] and succ [i] will then contain, respectively, the predecessor count and a pointer to the successors of object i. This allows the predecessor count and collection of successors of any object to be selected, taking constant time. Since we shall need to access the collection of successors of objects, we define access_succ(i,succ) as a basic operation that returns a pointer to the collection of successors of object i.
There are n collections of successors, one for each object. These may be stored separately or may share storage. This choice has important ramifications, which will be discussed later. For now, it is best to share storage and to implement each collection of successors as a list of records. The records consist of two integer fields, succobj, containing a successor object, and link, containing a pointer to the next list record. Either dynamic memory or an array may be used to store the records. Selecting the array for storage means the programmer must manage its allocation himself or herself. Dynamic memory is probably a more natural choice, but an array of records is used to illustrate its simple management in this case and to make the later discussion comparing shared or separate storage for the list records more concrete. Lists will be the array for record storage, and a variable t will keep track of the next available record in lists for task 3b. Since only insertions will be made into the lists, the entries of lists will be allocated one after another as needed, starting with the first. Thus t must be initialized correctly.
The apparent choice for the output ranking is an integer array rank, with a variable next specifying where the next output object is to be placed in the rank array. For convenience, we use the record ranking with the two fields rank and next.
The bag could be implemented similarly, in an array with bag pointing to the next available element for a new bag entry. When an object is to be removed from the bag, we can store its value in obj and then decrease bag by 1. Thus an object can be added or removed from the bag in constant time. This implementation is permissible because objects may be selected from the bag in any order. However, implementing the bag as in Figure 11.5 affords an advantage. By allowing the bag and the output ranking to share storage, it saves time. However, this selection is made primarily to emphasize a point to be made later about the independence of modules. In order to simplify the example, only the array entries starting with 1 are used. As you know, in C they start with zero; 0th array positions will not be used in this example so that ranking and array positions will be identical.
The X's represent nine objects placed in the rank array. Next, pointing to position 6, indicates that the next object to be selected from the bag will be the one in rank[next],rank[6] in this case. Bag, pointing to 10, indicates that when a successor is to be added to the bag, it should be placed in rank[bag],rank[10] in this case. In other words, the bag contains all objects in rank between next and bag-1.
The bag is initialized by traversing the count array and placing any object with zero count into the location of the rank array to which bag points. Bag, of course, must then be updated by 1 to move its pointer down. Bag must initially be 1, and next must initially be 1. Objects are then output in the order in which they are placed into the bag, easing processing and keeping the time constant for addition or removal of an object. Each time an object is selected, next must be increased by 1 to move it down. The bag is empty when next equals bag.
Before proceeding, phase I is illustrated by applying it to Example 11.6. For this example, count, succ, t, and list would appear as in Figure 11.6, after the first eight pairs have been input. Figure 11.7 graphically depicts the successor lists.
At the start of phase I, no information was processed yet on predecessors or successors for any object. The first pair, 7 3, contains the information that 3 has one more predecessor than was known, and that 7 has one more successor than was known, namely 3. One must be added to the count for 3, and 3 to the list of successors of 7, and so on for the other seven pairs.
The detailed processing of an input pair is illustrated for the last pair of this example. It is the ninth pair, 7 6. To update the count for 6, add 1 to count[6]. To create a record to contain the successor 6, place 6 into lists[9].succobj and add this new record to the current successor list for 7 by changing two pointers. First, copy the pointer from succ[7], the head of the list to which the new record is to be added, into the link field of the new record lists[9].link. Then place a pointer into succ[7] so that it points to the new record. In this case, 9 is placed into succ[7]. Since successors need not be kept in any special order, always adding records at the front of successor lists saves processing time. Adding the record anywhere else on the list would require traversal time from the head of the list to the insertion place. T must be incremented by 1 so that it points to the next available record in lists. The final situation after all nine input pairs have been read and processed is shown in Figures 11.8 and 11.9. An X indicates a null pointer.
We are now ready to consider the actual implementations for the functions of the data abstractions. Following is the code that might be used for those functions whose implementation may not be apparent.
increase
decrease
iszero
avail
insert
succinitialization
emptybag
remove
Note that avail must correctly initialize and update t.
Task 5b of the better (or "bag") refinement of the algorithm could be done by writing the procedure update from scratch. Instead, it is done here using a tool that is available, the traverse procedure of Chapter 3. First, traverse is modified by adding bag and count as additional parameters of both traverse and process, and changing its name to update.
Process, called by update, must now be implemented so that update does its job. Its code is
A complete program using topsort follows. Notice that topsort has two parameters. It is the same as our version, except it copies the rank field of ranking into the output array as a last step.
Because of the implementation, some functions must have access to specific variables. C requires these variables to be either passed as pointers or declared as global. For example, process must have access to rank, and emptybag to next. Incidentally, as written, topsort does not depend on the medium assumed for the input pairs. Normally, we want programs to be independent of the form of the input. This has been accomplished here for the pairs by using the function nextpair(i,j), which inputs the next pair and returns true if it is a nonsentinel pair. The program uses 0 0 as the sentinel pair.
Note that the ranking and bag implementations are not independent. Thus, if it is desirable to change the implementation of one, the other is also affected. As written, the bag acts as a stack, but it may be important to pick the entry to be removed from the bag more selectively. One way to do this is to implement the bag as a priority queue. In any case, to make ranking and bag independent requires changing their declarations, definitions, and basic operations.
We will now analyze the time requirements of this implementation. Refer to the refinement shown in the implementation that used data abstractions on page 503. Reading n takes constant time. The count and succ array initializations take time proportional to n. The while loop read and test takes constant time. Reading the next input pair and tasks 3a and 3b, which involve executing five instructions, take constant time. Each repetition of the loop thus takes constant time. Since the loop is executed once for each of the m input pairs, the total loop time will be proportional to m. Phase I thus takes some constant time, plus time proportional to n, plus time proportional to m.
Initializing the bag at the start of phase II takes time proportional to n, since it involves traversing the count array and placing each object whose count is zero into the bag. The while loop body of phase II, unlike that of phase I, does not take the same amount of time on every repetition. Task 5a takes constant time, but task 5b depends on the number of successors of the object that was removed by task 5a. The loop itself is executed n times, once for each object output.
How can we determine the total loop time required? Notice that each of the n objects will eventually be output in some loop execution. We do not know in what order the objects will be output. However, the time taken in its particular loop execution for each object output is the same. This time is at most a constant plus time proportional to the number of successors of the object. Thus, the total time for the while loop in phase II is the sum of the time required to output each object. The total time is then a constant times n plus time proportional to the sum
[(number of successors of object 1) plus (number of successors of object 2) . . . plus the (number of successors of object n)]
This sum is just the total number of successors, m. Hence the total time for phase II is made up of the same kinds of components as the total time for phase I. We conclude that the total time for this implementation has the same form.
Note that the search-based algorithm could take time O(n!). The straight-forward implementation of the construction-based algorithm could take time O(n
How much storage does the implementation require? Suppose the program is to run correctly for values of n between 1 and 20. The only difficulty in determining the actual amount of storage required is in deciding what length to declare for lists. This depends on how large m may be. In general, if there are n objects, each object can have no more than n - 1 successors--that is, an arrow to every other object. There are then at most n(n - 1) possible successors. Each successor requires one record of the lists array. Actually, because of the asymmetry property, at most one-half of the n(n - 1) possibilities can appear. Hence we need a total of at most 1/2
Knuth [1973a] and Wirth [1976] give different implementations of the algorithm for the topological sorting problem. See Aho, Hopcroft, and Ullman [1983] for a somewhat different point of view on its solution.
In the solution to the topological sorting problem, it is assumed that each distinct input pair appears only once and also that the input contains no loops. Either assumption might be violated. Of course, more obvious errors could occur. For example, n or one of the input pair members could be negative or out of range. It is not difficult to add a validation routine to check for these kinds of input errors. Subtler errors, such as replication of pairs or the occurrence of loops, are not as obviously remedied.
What does happen if pairs are replicated or loops occur in the input ? How would you recognize loops? Replication of an input pair i, j causes the count of j to be 1 larger than it should be. It also causes the successor j to appear on the list of successors of i one more time. When object i is eventually removed, its list of successors is traversed. This results in the count of j being reduced one additional time, so that the extra increase due to the i, j replication is cancelled. The implementation will thus work correctly as long as there is room for the extra successor records to appear in lists. If there is no room to accommodate these extra records, it is not possible to predict what will occur when the implementation is executed.
Loops, on the other hand, result in some objects never being output. Objects that are involved in a loop, or that are the successors of an object in a loop, will never have their counts go to zero, and will never appear in the bag of objects. In fact, had the test for completion been "S not empty" or "n objects output," loops in the input would cause an infinite loop in the program. It should now be clear that next-1, when the loop in phase II is exited, will be the actual number of objects that were output by the loop. If this is less than n, then loops occurred in the input. This can provide a simple test for loops.
As already noted, the implementation of the output ranking and the bag are coupled because they share storage. As a result they are not independent. This means that a change in the choice of implementation for one will affect the other. In general, such a situation is to be avoided--and, as pointed out earlier, could have been avoided. Certainly the small saving in time and storage did not warrant the added complexity.
There are, however, some important storage considerations that were alluded to earlier. Topsort will run out of storage before it runs out of time, since storage requirements grow as n2. The bulk of the storage needed is taken by the lists array. Suppose a maximum size, based on the available storage of the computer system, is declared for the lists array. Say its length is 50,000. Assuming each of its records takes two entries, this provides enough storage to guarantee the solution of any problem with no more than 25,000 successors (m
Suppose, instead, that the decision had been to represent each collection of successors by dedicating an array to the collection. Since the programmer does not know in advance how the successors will be distributed, each of the required n arrays should have the same length. Lists are no longer necessary, since the successors can be placed sequentially in the proper array. Of course, a variable will be needed to keep track of the last successor in each array. An additional array may be used for these pointers. If n is to be no greater than (say) 500, then each of the arrays containing the successors can be declared of length 50,000/500, or 100. The upshot is that the solution may now be guaranteed for a different class of problems. These problems must have n
Had dynamic memory been used instead of the lists array for storage of the successor records, the program would contain no explicit storage limitation (other than the declarations for the length of count, succ, and rank). Still, the maximum dynamic memory size would have imposed a limit on the value of m for which the program would execute.
One final point involving time and storage trade-offs. Suppose an input validation must be added to topsort just prior to the processing of the current i, j pair read in phase I. The function is to check whether i, j is a duplicate of an earlier input pair. If so, it is to be ignored; if not, it is to be processed. One way to accomplish this, which requires no additional storage, is to traverse the current list of successors of object i. If j appears on the list as a successor, then i, j is a duplicate; otherwise it is not. This takes time proportional to the current number of successors of i and thus adds a total time to phase I that is proportional to m2. Instead, the function can work in constant time if n(n - 1) additional storage is available. Use the storage for an n(n - 1) array that is initialized to all zeros. When i, j is read, simply test the (i, j)th array entry. If it is zero, the pair is not a duplicate. Then set the entry to 1 to indicate that this i, j pair has been processed. In this way, an entry of 1 will mean that the pair is a duplicate from now on. This adds total time to phase I of O(m) but requires n(n - 1) additional storage.
A topological sort produces a ranking of objects that satisfies constraints on their allowable positions within the ranking. The obvious algorithm for finding a topological sort, searching through all rankings until one satisfying the constraints is found, is not feasible. A feasible algorithm was developed by constructing a ranking that satisfied the constraints. The initial implementation merely produced an image of the input data in memory. It was improved significantly by using an array to contain predecessor counts, creating lists of successors, and introducing a bag to hold objects whose predecessor counts became zero. This solution was achieved by a process of stepwise refinement, stressing data abstraction, encapsulation, modularity, and the proper choice of data structures. The functional modularity of the final solution allowed immediate application of a routine developed earlier--the list traversal routine. Again, because of functional modularity, it was not difficult to determine where and how to build in appropriate checks of the input data.
More generally, the analysis of the storage and time requirements of a fairly complex program was demonstrated. Even though this cannot always be accomplished, or may be difficult for complex programs, it serves as an example of what we hope to be able to do.
1. Within a textbook, chapters cover specific topics. The information required to understand each topic is expected to have appeared before the topic appears in the book. Suppose you are given a list of topics and the other topics on which each depends. How might you select an ordering of the topics for their appearance in the book?
2. Which of these binary relations is a partial order on S?
a. "Square root of" on the set S of all real numbers greater than 1
b. "Is older than" on the set S of all your relatives
c. "Sits in front of" on the set S of all students in a class
d. "Lives diagonally across from" on the set S of all people
3. Write down the graphic representation for the binary relation R on the first 10 integers. R = (3, 2), (4, 6), (7, 6), (8, 1), (9, 7), (9, 8).
4. Write a detailed modification of the algorithm of Section 11.2 that will check if a given ranking is consistent with the given partial order.
5. Write a program to implement the refinement of Exercise 4 and determine its worst-case time and storage requirements.
6. Apply the construction-based algorithm of Section 11.3 to the following data to obtain a consistent ranking. Always select the smallest integer for output.
S = 1, 2, 3, . . . , 12
R = (3, 2), (4, 6), (7, 9), (12, 10), (5, 6), (2, 4), (8, 9), (2, 6), (3, 6), (7, 12), (3, 4), (7, 10)
7. If the second implementation of the construction-based algorithm is applied to the input of Exercise 6, what integers are in the bag after 3 is removed?
8. State clearly and concisely what purpose the bag serves in the better "bag" refinement and why it was introduced.
9. Write an expanded version of the better refinement that will output integers from the bag by selecting the smallest possible integer first.
10. What will the succ, lists and count arrays have in them after phase I, when the input pairs of the running example appear in the order 7 6, 5 3, 2 10, 6 8, 5 6, 7 3, 4 8, 7 1, 4 2?
11. What will the count, succ, and lists arrays look like after phase II as compared to after phase I?
12. Suppose the better implementation were modified so that no count array were stored in memory, and only the succ and lists arrays were available after phase I. Write a new phase II refinement under this constraint.
13. Suppose a solution to the topological sort problem had been constructed by determining what object should be at the bottom of the ranking. How would the better refinement be changed to reflect this new solution?
14. a. Suppose the bag is implemented in a separate record bag instead of using the ranking record. How must the data abstraction implementations change?
b. Suppose the output ranking is not kept in the ranking record but, instead, is simply printed. How must the program and data abstraction implementations change?
15. The function process is itself dependent on the ranking and bag implementations. Modify it so that process becomes independent of these implementations.
16. Suppose task 5b of the better refinement is further expanded to:
5b.i. For each successor of the output object, decrease its predecessor count by 1.
5b.ii. For each successor of the output object, if its predecessor count is zero, add the successor to the bag.
a. ow should the implementation of the data abstraction algorithm (on p. 503) be modified to reflect this refinement?
b. rite implementations for tasks 5b.i and 5b.ii that use traverse as a tool. This should include writing the corresponding two process functions.
c. ow will this expansion of task 5b affect the time required for the algorithm?
17. Suppose the input for Exercise 10 had the pairs below appended after 4 2. What would the graphic depictions of the successor lists be after phase I of topsort?
18. For the input of Exercise 17, what would be in the count array after phase I?
19. For the input of Exercise 17, show what will be in the count array, the successor lists, and the bag after 7 is output.
20. Take as input the Example 11.6 with pairs 10 4 and 10 1 appended after 4 2. What will the second implementation of topsort output in the rank array? What will be the value of next after phase II?
1. Write and run a program whose input will be a series of topological sorting problems. For each problem the program should execute a slight modification of the topsort function called newtopsort. Newtopsort has parameters n and topologicalsort. Newtopsort is to read in and echo print n and all input pairs for the example it has been called to work on. It should print out the relevant portions of the count, succ and lists arrays as they appear after phase I. When newtopsort returns, the program prints the topological sort contained in the topologicalsort array. Except for the modifications needed to do the printing, newtopsort corresponds exactly to the sample implementation of topsort, with one exception: Implement the bag as an array separate from rank. Newtopsort should work correctly for valid input and for any number of objects between 1 and 20. You should make up four input sample problems to use. Two should be valid. One should include replications, and one should contain loops.
2. Suppose, instead of using the sample implementation, you do the following to keep successor information: Declare lists to be an n(n - 1) two-dimensional array and keep the successors of object i in the ith row of lists. For the example, after phase I, lists would be This two-dimensional lists array takes up the same total amount of storage as the one-dimensional lists array of the better implementation. For both implementations, the limiting factor on whether or not the program will run might then be the value of n beyond which available storage is exhausted. Suppose you are willing to give up the guarantee that topsort will always run correctly. This means you may attempt to run problems whose n is large enough that you are not sure whether the implementation of lists can hold all successors. Discuss the relative advantages of the implementations.
3. This is the same as Assignment 1 except, instead of the lists array, use dynamic memory to store the successor lists.
4. Assume your program for Assignment 1 treated the bag with the operations empty-bag, remove, and baginitialization and count with the operations predinitialization and increase as data abstractions.
a. What does this mean?
b. Write a function, number, that also treats them as data abstractions and returns the number of objects in the bag when it is invoked. When it returns, the bag must contain exactly the same objects as before number was invoked. Assume number does not have access to information about the output ranking.
11.1.1 Binary Relations and Partial Orders
.
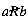for any a and b in S.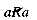
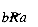
11.1.2 Graphic Representation of Partial Orders
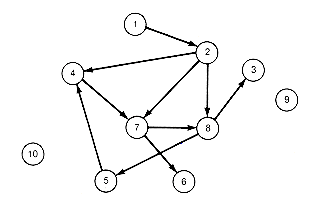
Figure 11.1 Binary Relation R on a Set of n = 10 Objects
11.1.3 Topological Sorts: Consistent Rankings
3
5 1 2 4 6 8 7
Figure 11.2 A Partial Order on the Integers 2, . . . , 9
10 value of n
7 3
5 3
2 10
6 8
5 6 m = 9 pairs
4 8
7 1
4 2
7 6
11.2: A Searching Solution
8 and 7 1, it is not a topological sort. Any ranking may be checked in this way. This leads to an obvious algorithm based on the generation of all rankings of the n objects.
X 2 X 1 distinct rankings of n objects. This product is n factorial. Consequently this solution can deal with values of n no greater than 16.* For larger n, an algorithm must be found that need not consider all rankings.11.3: A Constructed Solution
11.3.1 Correctness
Figure 11.3 Graphic Depiction of Example 11.6
j.11.3.2 An Initial Implementation
Figure 11.4 Result of Phase I of the First Refinement
11.3.3 A Better Implementation
Figure 11.5 Data Structure Implementation of Bag and Output-Ranking Data Abstractions
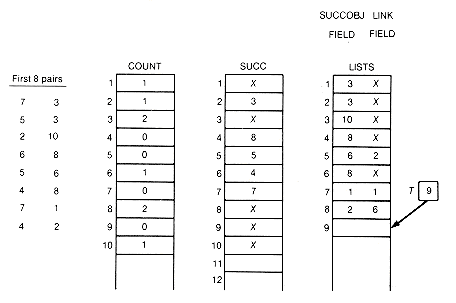
Figure 11.6 Data Structures Involved in Phase I after Input of First Eight Pairs
Figure 11.7 Graphic Depiction of Successor Lists
Figure 11.8 Data Structures of Figure11.7 after Processing Last Input Pair of Phase I
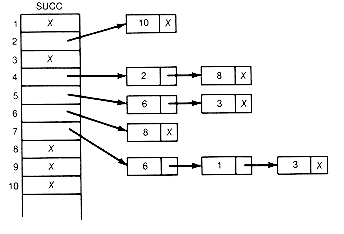
Figure 11.9 Graphic Depiction of Successor Lists of Figure 11.8
count[j] = count[j] + 1;
count[i] = count[i] - 1;
return(count[i] == 0);
static int t=0;
t++;
return(t);
pointer = avail();
setinfo(pointer,j);
setlink(pointer,succ[i]);
succ[i] = pointer;
for (i=1;i<=n;i++)
succ[i] = setnull();
emptybag =(bag == ranking.next);
*pobj = ranking.rank[ranking.next];
ranking.next = ranking.next + 1;
currentsucc = info(recordpointer);
decrease(currentsucc,count);
if(iszero(currentsucc,count))
{ranking.rank[*pbag] = currentsucc;
*pbag = *pbag + 1;
}
#defineLIMIT 21
typedef int outputarray[LIMIT];
main()
/* Reads the number of objects n and the input pairs
specifying a partial order on the objects, and prints
a topological sort of the n objects. Each pair should
not occur more than once in the input and n should
not exceed twenty. The sentinel pair is 0 0.
*/
{int n,i;
outputarray topologicalsort;
topsort(&n,topologicalsort);
printf("\n A TOPOLOGICAL SORT IS");for (i=1;i>=n;1++)
printf("\n %d",topologicalsort[i]);}
typedef int countcollection[LIMIT];
predinitialization(n,count)
/* Initializes all n counts to zero. */
int n;
countcollection count;
{int i;
for (i=1;i<=n;i++)
count[i] = 0;
}
increase(j,count)
/* Increases the jth count by one. */
int j;
countcollection count;
{count[j] = count[j] + 1;
}
decrease(j,count)
/* Decreases the jth count by one. */
int j;
countcollection count;
{count[j] = count[j] - 1;
}
iszero(i,count)
/* Returns true only if the ith count is zero. */
int i;
countcollection count;
{return(count[i] == 0);
}
#define RECORDLIMIT 191
/* RECORDLIMIT should be at least
(((LIMIT-1)*(LIMIT-2))/2)+1
*/
#define NULL - 1
typedef int listpointer;
typedef struct
{int succobj;
listpointer link;
}listrecords,recordsarray[RECORDLIMIT];
recordsarray lists;
listpointer setnull()
/* Returns a null pointer. */
{return(NULL);
}
anotherrecord(recordpointer)
/* Returns true only if recordpointer
points to a record.
*/
listpointer recordpointer;
{return(recordpointer != NULL);
}
info(pointer)
/* Returns the contents of the succobj field
of the record pointed to by pointer.
*/
listpointer pointer;
{return(lists[pointer].succobj);
}
listpointer next(pointer)
/* Returns the link field value of
the record pointed to by pointer.
*/
listpointer recordpointer;
{return(lists[recordpointer].link);
}
setinfo(pointer,value)
/* Copies value into the succobj field
of the record pointed to by pointer.
*/
listpointer pointer;
int value;
{lists[pointer].succobj = value;
}
setlink(pointer1,pointer2)
/* Copies pointer 2 into the link field
of the record pointed to by pointer 1.
*/
listpointer pointer1,pointer2;
{lists[pointer 1].link = pointer2;
}
listpointer avail()
/* Returns a pointer to storage allocated
for a list record.
*/
{static int t=0;
t++;
return(t);
}
typedef listpointer succ_collection[LIMIT];
insert(i,j,succ)
/* Add j into the ith collection in succ. */
int i,j;
succ_collection succ;
{listpointer pointer,avail();
pointer = avail();
setinfo(pointer,j);
setlink(pointer,succ[i]);
succ[i] = pointer;
}
succinitialization(n,succ)
/* Initializes all n collections of succ to empty. */
int n;
succ_collection succ;
{int i;
listpointer setnull();
for (i=1;i<=n;i++)
succ[i] = setnull();
}
listpointer access_succ(i,succ)
/* Returns a pointer to the i collection in succ. */
int i;
succ_collection succ;
{return(succ[i]);
}
typedef struct
{outputarray rank;
int next;
}rankingrecord;
rankingrecord ranking;
1 allocates storage for ranking
copy(n,topologicalsort,ranking)
/* Copies the rank field of ranking
into topologicalsort.
*/
int n;
outputarray topologicalsort;
rankingrecord ranking;
{int i;
for (i=1;i<=n;i++)
topologicalsort[i] = ranking.rank[i];
}
typedef int bagcollection;
baginitialization(pbag,n,count)
/* Initializes the bag so it contains
only objects whose counts are zero.
*/
bagcollection *pbag;
int n;
countcollection count;
{int i;
ranking.next = 1;
*pbag = 1;
for(i=1;i<=n;i++)
if(iszero(i,count))
{ranking.rank[*pbag] = i;
*pbag = *pbag + 1;
}
}
emptybag(bag)
/* Returns true only if bag is empty. */
bagcollection bag;
{return(bag == ranking.next);
}
remove(pbag,pobj)
/* Sets obj to an object to be removed
from bag, and removes it.
*/
bagcollection *pbag;
int *pobj;
{*pobj = ranking.rank[ranking.next];
ranking.next = ranking.next + 1;
}
process(listname,recordpointer,pbag,count)
/* Decreases the count of the successor pointed
to by recordpointer and adds it to the bag if
its count has become zero.
*/
listpointer listname,recordpointer;
bagcollection *pbag;
countcollection count;
{int currentsucc;
currentsucc = info(recordpointer);
decrease(currentsucc,count);
if (iszero(currentsucc,count))
{ranking.rank[*pbag] = currentsucc;
*pbag = *pbag + 1;
}
}
topsort(pn,topologicalsort)
/* Inputs the number of objects n and the
partial order and generates a solution in
topologicalsort.
*/
int *pn;
outputarray topologicalsort;
{countcollection count;
succ_collection succ;
bagcollection bag;
int i,j,obj;
printf("\n enter n between 1 and %d\n",LIMIT-1);scanf("%d",pn);predinitialization(*pn,count);
succinitialization(*pn,succ);
while (nextpair(&i,&j))
{increase(j,count);
insert(i,j,succ);
{baginitialization(&bag,*pn,count);
while(!emptybag(bag))
{remove(&bag,&obj);
update(succ,obj,&bag,count);
}
copy(*pn,topologicalsort,ranking);
}
nextpair(pi,pj)
int*pi,*pj;
/* Input the next pair and return true
only if it was not the sentinel pair.
*/
{print("\n enter a pair \n");scanf("%d %d",pi,pj);return(!((*pi == 0) && (*pj == 0)));
}
update(succ,obj,pbag,count)
/* Update the counts of all successors of obj
and place any whose counts become zero
into bag.
*/
succ_collection succ;
int obj;
bagcollection *pbag;
countcollection count;
{listpointer listname,recordpointer,access_succ();
listname = access_succ(obj,succ);
recordpointer = listname;
while(anotherrecord(recordpointer))
{process(listname,recordpointer,pbag,count);
recordpointer = next(recordpointer);
}
}
11.4: Analysis of Topsort
m). Topsort takes time of the form c1 + c2n + c3m and represents a very substantial improvement. It was made possible because we were able to determine precisely, and to obtain efficiently, the information required to do the processing steps of the algorithm. The topological sort problem is more complex than earlier ones in this book, but it illustrates the same theme. The processing to be done determines the data structures that are most appropriate. Clearly, any implementation of an algorithm that does topological sorting must take time of the form an + bm, since it is necessary to read in all m input pairs and output all n objects. n(n - 1) records for lists. If n is 20, then (20 19)/2 records will do. The storage required is proportional to n2.11.5: Behavior for Replicated Pairs or Loops
11.6: Final Comments on Topsort
25,000). It makes no difference how the successors are distributed among the objects; only the total number is relevant. 500, and each object may have no more than 100 successors. Even though the total number of successors may now be 50,000 (twice as many as before), their distribution is critical. When storage is at a premium, such considerations are important.11.6.1 An Input Validation
11.7: Reviewing Methodology
Exercises
7 3, 5 6, 4 2, 7 3, 6 8
Suggested Assignments
