15.1 INTRODUCTION
In the standard Boolean retrieval model, each document is associated with a set of keywords or index terms, and each query is in the form of a Boolean expression. The Boolean expression consists of a set of index terms connected by the Boolean operators and, or, and not. The documents retrieved for a given query are those that contain index terms in the combination specified by the query. As can be seen from the discussion in Chapter 10, the Boolean model is popular in operational environments because it is easy to implement and is very efficient in terms of the time required to process a query. Boolean retrieval systems are also capable of giving high performance in terms of recall and precision if the query is well formulated. However, the model has the following limitations, as discussed by a number of authors: Bookstein (1985), Cater & Kraft (1987), Cooper (1988), Wong et al. (1988), Paice (1984), Salton, Fox & Wu (1983).
 The Boolean model gives counterintuitive results for certain types of queries. For example, consider a query of the form A and B and C and D and E. A document indexed by all but one of the above terms will not be retrieved in response to this query. Intuitively, it appears that the user would be interested in such a document, and that it should be retrieved. Similarly, for a query of the form A or B or C or D or E, a document indexed by any of these terms is considered just as important as a document indexed by some or all of them. This limitation of the Boolean model is due to its strict interpretation of the Boolean operators. Our experimental studies have shown that such a strict interpretation is not compatible with the user's interpretation; for example, results of the retrieval based on a strict interpretation have lower precision than results from a P-norm interpretation as shown by Salton, Fox & Wu (1983). Hence, we need to soften the Boolean operators, and account for the uncertainties that are present in choosing them. We can do this by making the and query behave a bit like the or query and the or query behave somewhat like the and query.
The Boolean model gives counterintuitive results for certain types of queries. For example, consider a query of the form A and B and C and D and E. A document indexed by all but one of the above terms will not be retrieved in response to this query. Intuitively, it appears that the user would be interested in such a document, and that it should be retrieved. Similarly, for a query of the form A or B or C or D or E, a document indexed by any of these terms is considered just as important as a document indexed by some or all of them. This limitation of the Boolean model is due to its strict interpretation of the Boolean operators. Our experimental studies have shown that such a strict interpretation is not compatible with the user's interpretation; for example, results of the retrieval based on a strict interpretation have lower precision than results from a P-norm interpretation as shown by Salton, Fox & Wu (1983). Hence, we need to soften the Boolean operators, and account for the uncertainties that are present in choosing them. We can do this by making the and query behave a bit like the or query and the or query behave somewhat like the and query.
 The standard Boolean model has no provision for ranking documents. However, systems combining features of both the Boolean and the vector models have been built to allow for ranking the result of a Boolean query, for example, the SIRE system (1977) Noreault, Koll & McGill. Ranking the documents in the order of decreasing relevance allows the user to see the most relevant document first. Also, the user would be able to sequentially scan the documents, and stop at a certain point if he/she finds that many of the documents are no longer relevant to the query.
The standard Boolean model has no provision for ranking documents. However, systems combining features of both the Boolean and the vector models have been built to allow for ranking the result of a Boolean query, for example, the SIRE system (1977) Noreault, Koll & McGill. Ranking the documents in the order of decreasing relevance allows the user to see the most relevant document first. Also, the user would be able to sequentially scan the documents, and stop at a certain point if he/she finds that many of the documents are no longer relevant to the query.
 During the indexing process for the Boolean model, it is necessary to decide whether a particular document is either relevant or nonrelevant with respect to a given index term. In the Boolean model, there is no provision for capturing the uncertainty that is present in making indexing decisions. Assigning weights to index terms adds information during the indexing process.
During the indexing process for the Boolean model, it is necessary to decide whether a particular document is either relevant or nonrelevant with respect to a given index term. In the Boolean model, there is no provision for capturing the uncertainty that is present in making indexing decisions. Assigning weights to index terms adds information during the indexing process.
 The Boolean model has no provision for assigning importance factors or weights to query terms. Yet, searchers often can rate or rank index terms in queries based on how indicative they are of desired content. It would be useful to allow weights to be assigned to (some) query terms, to indicate that the presence or absence of a particular query term is more important than that of another term.
The Boolean model has no provision for assigning importance factors or weights to query terms. Yet, searchers often can rate or rank index terms in queries based on how indicative they are of desired content. It would be useful to allow weights to be assigned to (some) query terms, to indicate that the presence or absence of a particular query term is more important than that of another term.
Many retrieval models have been proposed as alternatives to the Boolean model. This chapter discusses three such models:
 MMM
MMM
 Paice
Paice
 P-norm
P-norm
These models avoid the strict interpretation of the Boolean operators, and attempt to provide a ranking of the retrieved documents in order of decreasing relevance to the query. They attempt to take into account the uncertainty involved in the indexing process. In addition, the P-norm model has the ability to consider weighted query terms. Experimental results have shown that these models can given an improvement of more than 100 percent in precision, at fixed recall levels, over the standard Boolean model as reported in Lee (1988).
We begin with a description of each model, and then discuss the data structures and algorithms that implement them. A few examples of the similarity computation in each model are also provided. We conclude with a short discussion of the relative merits of these models.
15.2 EXTENDED BOOLEAN MODELS
In the three models discussed below, a document has a weight associated with each index term. This document weight is a measure of the degree to which the document is characterized by that term. Without loss of generality, we assume that document weights for all index terms lie in the range [0, 1]. This is less restrictive than in the standard Boolean model, which limits the values to the extremes of the range, namely 0 and 1.
To retrieve documents relevant to a given query, we need to calculate the query-document similarity for documents in the collection. The query-document similarity is an attempt to predict the relevance of a document to the query. In the following subsections, we consider each model and its method for calculating similarity.
15.2.1 The MMM model
This model is based on the concept of fuzzy sets proposed by Zadeh (1965). In fuzzy-set theory, an element has a varying degree of membership, say dA, to a given set A instead of the traditional membership choice (is an element/is not an element).
In the Mixed Min and Max (MMM) model developed by Fox and Sharat (1986), each index term has a fuzzy set associated with it. The document weight of a document with respect to an index term A is considered to be the degree of membership of the document in the fuzzy set associated with A. The degree of membership for union and intersection are defined as follows in Fuzzy set theory:
According to fuzzy set theory, documents that should be retrieved for a query of the form A or B, should be in the fuzzy set associated with the union of the two sets A and B. Similarly, the documents that should be retrieved for a query of the form A and B, should be in the fuzzy set associated with the intersection of the two sets. Hence, it is possible to define the similarity of a document to the or query to be max(dA, dB), and the similarity of the document to the and query to be min(dA, dB). The MMM model attempts to soften the Boolean operators by considering the query-document similarity to be a linear combination of the min and max document weights.
Thus, given a document D with index-term weights dA1, dA2, . . . , dAn for terms A1, A2, . . . , An, and the queries
the query-document similarity in the MMM model is computed as follows:
where Cor1, Cor2 are "softness" coefficients for the or operator, and Cand1, Cand2 are softness coefficients for the and operator. Since we would like to give the maximum of the document weights more importance while considering an or query and the minimum more importance while considering an and query, generally we have Cor1 > Cor2 and Cand1 > Cand2. For simplicity it is generally assumed that Cor1 = 1 - Cor2 and Cand1 = 1 - Cand2.
Our experiments (Lee & Fox 1988) indicate that the best performance usually occurs with Cand1 in the range [0.5, 0.8] and with Cor1 > 0.2. In general, the computational cost is low, and retrieval effectiveness is good, much better than with the standard Boolean model, as can be seen from Table 15.1 in section 15.4 below.
The model proposed by Paice (1984) is also based on fuzzy-set theory. It is similar to the MMM model in that it assumes that there is a fuzzy set associated with each index term, and the document weight of a document with respect to an index term represents the degree of membership of the document with respect to the fuzzy set associated with that index term. However, while the MMM model considers only the maximum and the minimum document weights for the index terms while calculating the similarity, the Paice model takes into account all of the document weights.
Thus, given a document D with index-term weights dA1, dA2 ,. . . , dAn for terms A1, A2, . . . , An, and the queries
the query-document similarity in the Paice model is computed as follows:
where the di's are considered in descending order for or queries and in ascending order for and queries. Note that when n = 2, the Paice model behaves like the MMM model.
The experiments conducted by Lee & Fox (1988) have shown that setting the value of r to 1.0 for and queries, and to 0.7 for or queries, gives good retrieval effectiveness. The computational cost for this model is higher than that for the MMM model. This is because the MMM model only requires the determination of min or max of a set of term weights each time an and or or clause is considered, which can be done with an O(n) algorithm as described in Aho and Ullman (1974). The Paice model requires the term weights to be sorted in ascending or descending order, depending on whether an and clause or an or clause is being considered. This requires at least an 0(n log n) sorting algorithm. A good deal of floating point calculation is needed also.
Besides allowing document weights for index terms, the P-norm model also allows query terms to have weights. In the P-norm model, a document D with weights dA1, dA2, . . . , dAn with respect to index terms Al, A2, . . . , An is considered to be a point with coordinates (dA1, dA2, . . . , dAn) in an n-dimensional space. These document weights are generally obtained using term frequency and inverse document frequency statistics, with proper normalization as described by Fox (1983).
Consider an or query of the form dA1 or dA2 . . . or dAn. It is clear that the point having all the n coordinates equal to 0 (indicating that all the index terms are absent) is to be avoided for this query, whereas for an and query of the form dA1 and dA2. . . and dAn, the point with all the n coordinates equal to 1 (indicating that all the index terms have weight 1) is the most desirable point. Thus, it is possible to rank the documents (i.e., from those with highest similarity to those with lowest similarity) in order of decreasing distance from the point (0, 0, . . . , 0) for an or query, and in order of increasing distance from the point (1, 1, . . . , 1) for an and query.
In the P-norm model, the generalized queries are of the form:
We note that the operators have coefficients P which indicate the degree of strictness (from 1 for least strict to
The query-document similarity for the P-norm model is calculated using the following formulae:
Numerous experiments have shown the P-norm model to be very effective as reported in Salton, Fox & Wu (1983), Fox & Sharat (1986), Lee & Fox (1988), Fox (1983). However, when the P-value is greater than one, the computational expense can be high. This is because of the need for expensive exponentiation computations.
As in any other information retrieval system, we need to convert the given set of documents and queries into a standard format. We first discuss the data structures used in our implementation, and then follow up with a discussion of the actual algorithms.
There are several important data structures for both the document and query representations.
Given a set of documents, the goal is to index them, that is, find the index terms in the collection, and assign document weights for each document with respect to each index term. To calculate the document weight for an index term, a weighting technique such as normalized (tf * idf)ik can be used. A more detailed discussion of weighting techniques is provided in Chapter 10. The data structure for a document consists of an array doc _wts that stores the document weights as shown below. The element doc_wt [i] is the document weight for the ith index term.
We assume that each query has an id associated with it, and is in the form of a tree with the operators as internal nodes and index terms as the leaves (see Figure 15.1). The data structure used to store a query is as follows:
We see from the query structure that there are three arrays associated with each query (see Figure 15.2):
In the query structure we store the address of the first element of each array. In our implementation we assume that the first element of the node array is the root of the query tree.
The tree-node structure is as follows:
In this structure, the child_index is the index of the leftmost child of the current node within the array of nodes. Similarly, sibling_index is the index of the next node to the right of the current node within the array of nodes. If a node does not have any children / siblings to its right, the value of its child_index / sibling_index will be equal to UNDEF (-1).
It is possible to determine whether the current node is an operator node or an index-term node by examining the value of child_index (see Figure 15.3). Since index terms can only be leaves of the tree, they cannot have any children, whereas operators will have at least one child. Hence, if child_index has value UNDEF, then it implies that the current node is an index-term node; otherwise it implies that the node is an operator node. The iterm_op_index in the TREE_NODE structure is the index number of the index-term/operator associated with the current node within the array of index-term/operators.
The data structure that stores information about an index term is as follows:
Here, iterm_num is the unique number given to an index term. Note that iterm_wt, which is the weight of the index term in the query, is used only for P-norm queries.
The data structure for an operator is as follows:
If the MMM model is being used, then op_coeff is the Cor1 / Cand1 value. (Note: We assume that Cor2 = 1 - Cor1 and Cand2 = 1 - Cand1.) If on the other hand the Paice model is being used, then the op_coeff is the r value. If the P-norm model is being used, then op_coeff is the P-value.
Given a query and a set of documents in the standard form, we use the following algorithm to retrieve and rank documents:
In order to calculate the query-document similarity, we start from the root of the query tree, and find the similarity for each child. (Refer to the appendix for the C program.) If the child is an index term, then the similarity is the document weight for that index term. If it is an operator, then we recursively calculate the similarity for each child of that node. Once the similarity value is determined for a child, further processing is different for the various models and is described below:
We update the values of two variables, maximum and minimum (both of type double), where
We store the similarity in an array (of type double), child_sims, which will contain the similarities of the children of the current node.
We update the values of two variables, numerator and denominator (both of type double), where
Once all the children of the node have been considered, we use the appropriate formula to find the actual similarity.
For example, if the document weights for the index terms A, B, and C in a query Q of the form A or B or C and for a particular document D are 0.5, 0.8, and 0.6, respectively, then the maximum of the three is 0.8, and the minimum 0.5. If the coefficient of the or operator is 0.7, then, using the above formula, the MMM similarity between the given document and query is
If the Paice similarity is being calculated, we begin by sorting the array child_sims in descending order for an OR node, and in ascending order for an AND node. We then use the following formula to calculate the Paice query-document similarity.
For the query Q given above, since the operator is OR_OP we sort the similarities in descending order. We will therefore have the similarities in the order: 0.8, 0.6, 0.5. Hence, using the formula given above, with the assumption that r = 0.7, the Paice similarity between the given document and query will then be
If for the query Q given above, the query term weights are 0.5 and the operator coefficient or the P or operator has the coefficient value is 2, then the value of the numerator and denominator after considering the three index terms will be
Using the final values of the numerator and denominator and the formula given above, the query-document similarity SIM (Qor, D) will be
The C programs that implement these algorithms are given in the appendix. The routine cal_sim() is called with the array containing the document weights which are of type float as the first parameter, the query vector which is of type QUERY_STRUCT as the second parameter, and the third argument sim_type which determines the type of similarity being computed, that is, MMM, Paice, or P-norm. Based on the value of the third parameter, one of the following sets of routines is called for further computations:
Numerous experiments performed with the extended Boolean models have shown that they give much better performance than the standard Boolean model as reported by Lee & Fox (1988). Table 15.1 gives the percentage improvement in the average precision that these models showed over the standard Boolean model for three test collections: the CISI, CACM, and the INSPEC collections. As can be seen in the table, all three models show substantial improvement over the standard Boolean model. In fact, for the CACM and the INSPEC collections, all three models show more than 100 percent improvement.
The P-norm model is computationally expensive because of the number of exponentiation operations that it requires. The Paice model requires one to sort the similarities of the children. This adds to its computational overhead. The MMM model clearly has the least computational overhead of the three models.
The standard Boolean model is still the most efficient model. But by using any one of the extended Boolean models, it is possible to get much better performance. Based on experimental studies, the MMM model appears to be the least expensive, while the P-norm model gives the best results in terms of average precision.
AHO, A. J., and J. ULLMAN. 1974. "The Design and Analysis of Computer Algorithms." Reading, Mass.: Addison-Wesley.
BOOKSTEIN, A. 1985. "Probability and Fuzzy-Set Applications to Information Retrieval," in M. E. Williams, ed., Annual Review of Information Science and Technology (ARIST), 20, 117-51.
CATER, S. C., and D. H. KRAFT. 1987, June. "TIRS: A Topological Information Retrieval System Satisfying the Requirements of the Waller-Kraft Wish List." Presented at the 10th Annual Int'l ACM-SIGIR Conference on R&D in Information Retrieval, 171-80.
COOPER, W. S. 1988. "Getting Beyond Boole." Information Processing & Management 24(3), 243-48.
FOX, E. A. 1983. "Extending the Boolean and Vector Space Models of Information Retrieval with P-Norm Queries and Multiple Concept Types." Cornell University, August.
FOX, E. A., and S. SHARAT. 1986. "A Comparison of Two Methods for Soft Boolean Interpretation in Information Retrieval." Technical Report TR-86-1, Virginia Tech, Department of Computer Science.
LEE, W. C., and E. A. FOX. 1988. "Experimental Comparison of Schemes for Interpreting Boolean Queries." Virginia Tech M.S. Thesis, Technical Report TR-88-27 Department of Computer Science.
NOREAULT, T., M. KOLL, and M. J. MCGILL. 1977. "Automatic Ranked Output from Boolean Searches in SIRE." J. American Society for Information Science, 28(6), 333-39.
PAICE, C. P. 1984. "Soft Evaluation of Boolean Search Queries in Information Retrieval Systems." Information Technology, Res. Dev. Applications, 3(1), 33-42.
SALTON, G., E. A. FOX, and H. WU. 1983. "Extended Boolean Information Retrieval." Communications of the ACM, 26(12), 1022-36.
WONG, S. K. M., W. ZIARKO, V. V. RAGHAVAN, and P. C. N. WONG. 1988. "Extended Boolean Query Processing in the Generalized Vector Space Model." Information Systems 14(1), 47-63.
ZADEH, L. A. 1965. "Fuzzy Sets," Information and Control, 8, 338-53.
dA
 B = min(dA, db)
B = min(dA, db)dA
 B = max(dA, db)
B = max(dA, db)Qor = (A1 or A2 or . . . or An) and
Qand = (A1 and A2 and . . . and An),
SlM(Qor, D) = Cor1 * max(dA1, dA2, . . . , dAn) + Cor2 * min(dA1, dA2, . . . , dAn)
SlM(Qand, D) = Cand1 * min(dA1, dA2, . . . , dAn) + Cand2 * max(dA1, dA2 . . . , dAn)
15.2.2 The Paice Model
Qor = (A1 or A2 or ... An) and
Qand = (A1 and A2 and ... and An)
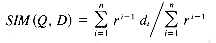
15.2.3 The P-norm Model
Q or p = (A1, a1) orP (A2, a2) orP ... orP (An, an), and
Q and p = (A1, a1) andP (A2, a2) andP ... andP (An, an).
 for most strict, i.e., the Boolean case) of the operator. Also, the query terms have weights (i.e., ai) which indicate their relative importance. Sophisticated users may wish to assign the P-values and query weights. Extensive experimentation demonstrated that system-assigned p-values (e.g., p = 2 throughout a query) can give good results, and that uniform query weighting of 1 or based on inverse document frequency will lead to effective retrieval as described by Fox (1983).
for most strict, i.e., the Boolean case) of the operator. Also, the query terms have weights (i.e., ai) which indicate their relative importance. Sophisticated users may wish to assign the P-values and query weights. Extensive experimentation demonstrated that system-assigned p-values (e.g., p = 2 throughout a query) can give good results, and that uniform query weighting of 1 or based on inverse document frequency will lead to effective retrieval as described by Fox (1983).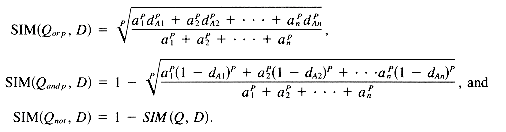
15.3 IMPLEMENTATION
15.3.1 Data Structures
Document structure
typedef struct
{float doc_wts[NUM_ITERM]; /*document weight vector*/
} DOC_STRUCT
Query Structure
typedef struct
{ long query_id; /* query id */TREE_NODE *beg_node _array; /* array of query nodes */
ITERM_TUPLE *beg_iterm_array; /* array of index terms */
OP_TUPLE *beg_op_array; /* array of operators */
} QUERY_STRUCT
 an array of the nodes in the query tree
an array of the nodes in the query tree an array of index terms
an array of index terms an array of operators
an array of operators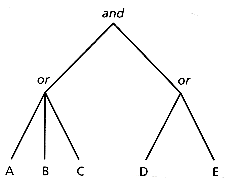
Figure 15.1: Structure of query (A or B or C) and (D or E)
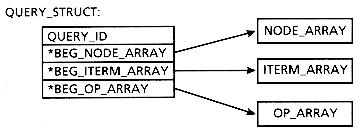
Figure 15.2: Structure of QUERY-STRUCT
typedef struct
{int iterm_op_index; /* index of index-term/operator for
leaf/non-leaf node resp. */
short child_index; /* index of the left child of the
current node */
short sibling_index; /* index of right sibling of the
current node */
} TREE_NODE /* structure of a node in the query tree */
typedef struct
{long iterm_num; /* unique ID given to index-term */
float iterm_wt; /* weight of the index-term */
} ITERM_TUPLE /* structure of an index term */

Figure 15.3: Data structures generated for query ((A or B or C) and (D or E))
typedef struct
{int op_type; /* type ot operator -
AND_OP / OR_OP / NOT_OP */
long op_coeff; /* coefficient of the operator -
= 0.0 for NOT_OP
= C_or1 / C _and1 for MMM model,
= r value for Paice model, and
= P value for P-norm model */
float op_wt; /* wt. of the operator */
} OP_TUPLE /* structure of an operator */
15.3.2 Algorithms and Examples
For each document
Find similarity;
Sort similarities;
Display document / similarity data in descending order.
 For the MMM model:
For the MMM model:maximum = max(dA1 dA2,...,dAn), and
minimum = min(dA1 dA2,...,dAn).
 For the Paice model:
For the Paice model: For the P-norm model:
For the P-norm model: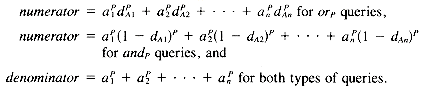
 For the MMM model, we can calculate the similarity for the node by using the following formula:
For the MMM model, we can calculate the similarity for the node by using the following formula:SIM(Q,D) = Cop * maximum + (1 - Cop) * minimum,
SIM(Q,D) = 0.7 * 0.8 + (1 - 0.7) * 0.5 = 0.71
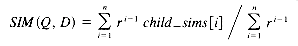
SIM(Q,D) = 0.70*0.8 + 0.71*0.6 + 0.72*0.5/0.70 + 0.71 + 0.72
= 1.465/2.19 = 0.6689
 If the P-norm similarity is being calculated, then we use the values of the numerator and denominator in the following formula to calculate the P-norm query-document similarity:
If the P-norm similarity is being calculated, then we use the values of the numerator and denominator in the following formula to calculate the P-norm query-document similarity:SIM(Qor,D) = (numerator/denominator)1/p_value
SIM(Qand,D) = 1 - (numerator/denominator)1/p_value
Index Term Numerator Denominator
1 A 0 + 0.52 * 0.52 0 + 0.52
= 0.0625 = 0.25
2 B 0.0625 + 0.52 * 0.82 0.25 + 0.52
= 0.2225 = 0.50
3 C 0.225 + 0.52 * 0.62 0.50 + 0.52
= 0.3125 = 0.75.
SIM(Qor,D) = (0.3125/0.75)1/2 = 0.6455
 mmm_sim( ): MMM model
mmm_sim( ): MMM model paice_sim( ): Paice model
paice_sim( ): Paice model update_numer_denom( ) & p_norm_sim( ): P-norm model
update_numer_denom( ) & p_norm_sim( ): P-norm model15.4 CONCLUSION
Table 15.1: Percentage Improvements Over Standard Boolean Model Test Collection
Scheme CISI CACM INSPEC
------------------- ------------------ ------------------
Best Average Best Average Best Average
Precision Rank Precision Rank Precision Rank
-------------------------------------------------------------------
P-norm 79 1 106 2 210 1
Paice 77 2 104 3 206 2
MMM 68 3 109 1 195 3
REFERENCES
APPENDIX
/**
** Compute query-document similarity using MMM, Paice and P-norm
** formulas
**/
#include <stdio.h>
#include <math.h>
#define UNDEF-l
#define NOT_OP -2
#define AND_OP -3
#define OR_OP -4
#define MMM_SIM 1
#define PAICE_SIM 2
#define P_NORM_SIM 3
#define P_INFINITY 0.0 /* Used only for P-norm model */
typedef struct
{long iterm_num; /* Unique ID given to the index-term */
float iterm_wt; /* Weight of index-term (P-norm queries only) */
} ITERM_TUPLE; /* Structure of an index-term in a query */
typedef struct
{int op_type; /* operator type - AND_OP, OP_OP, NOT_OP */
float op_coeff; /* Coefficient of the operator
= 0.0 for NOT_OP,
= C_or1/C_and1 for MMM model,
= r value for Paice model, and
= P value for P-norm model */
float op_wt; /* Wt. of operator - (P-norm queries only) */
} OP_TUPLE; /* Structure of an operator in a query */
typedef struct
{long iterm_op_index; /* If child_index = UNDEF then concept
index, else operator index */
short child_index; /* Current node's left child index */
short sibling_index; /* Current node's right sibling index */
} TREE_NODE; /* Structure of a node in the query tree */
typedef struct
{long query_id; /* Query id */
TREE_NODE *beg_node_array; /* Array of query nodes */
ITERM_TUPLE *beg_iterm_array; /* Array of index terms */
OP-TUPLE *beg_op_array; /* Array of operators */
} QUERY-STRUCT; /* Structure of a query */
#define NUM_ITERMS 1000 /* Max. no. of index-terms
allowed in a document */
/***************************************************************************
double
calc_sim ( doc_wts, query_vec, sim_type )
Returns: The MMM / Paice / P-norm similarity between the given
document and query.
Purpose: To compute:
MMM_SIM (Doc, Query ) if sim_type = MMM_SIM, or
PAICE_SIM (Doc, Query ) if sim_type = PAICE_SIM, or
P_NORM_SIM (Doc, Query ) if sim_type = P_NORM_SIM,
Plan: Call the routine to calculate the similarity by passing
to it the index of the root of the query tree (= zero).
***************************************************************************/
double
calc_sim ( doc_wts, query_vec, sim_type )
float doc_wts[NUM_ITERMS]; /* In: doc. weights vector */
register QUERY_STRUCT *query_vec; /* In: Given Query vector */
short sim_type; /* In: Similarity type flag */
{double calc_tree_sim ();
if ( ( sim_type != MMM_SIM ) && ( sim_type != PAICE-SIM ) &&
( sim_type != P_NORM_SIM ) )
fprintf ( stderr, "calc_sim: illegal similarity\
type %d, query %d\n", sim_type,
query_vec-> query_id );
return ( calc_tree_sim (doc_wts, query_vec, 0, sim_type ) );
}
/***************************************************************************
static double
calc_tree_sim ( doc_wts, query_vec, root_index, sim_type )
Returns: The similarity between the given document and the
subtree of the query tree with its root at ROOT_INDEX
Purpose: To compute: SIM (Doc, Query-subtree)
Plan: If the root of the subtree is an index-term then
similarity is the document wt. for that index-term
else, if it is an operator then,
if the operator == NOT_OP then
(1) Calculate the similarity of the child of
the current node (CHILD_VALUE)
(2) Return (1.0 - CHILD_VALUE)
else if the operator == AND_OP or OR_OP then
(1) Calculate the similarity considering
each child of the current node
(2) If (SIM_TYPE == MMM_SIM) then
Find the maximum and the minimum of
these similarities,
else if (SIM_TYPE == PAICE_SIM) then
Store this similarity in the array
child_sims,
else if (SIM_TYPE == P_NORM_SIM) then
Find the numerator and denominator
to be used in the formula
else
Print "invalid sim_type".
(3) Use the appropriate similarity computation
formula to compute the similarity for
the current node.
***************************************************************************/
static double
calc_tree_sim ( doc_wts, query_vec, root_index, sim_type)
float doc_wts [NUM_ITERMS]; /* In: Document weights */
register QUERY_STRUCT *query_vec; /* In: Query vector */
short root_index; /* In: Index of the root of the
subtree to be evaluated */
short sim_type; /* In: Similarity type flag */
{register TREE_NODE *root_ptr; /* Addr. of the root of the
subtree being considered */
register TREE_NODE *child_ptr; /* Addr. of a child of the root
of subtree being considered */
register OP_TUPLE *op_ptr; /* Addr. of current operator */
register ITERM_TUPLE *iterm_ptr; /* Addr. of current index-term */
long doc_index; /* Index of the weight of the
current index-term within
DOC-WTS array */
short child_index; /* Index of the child of the root
within the set of tree nodes */
double child_value; /* Sim. of child's subtree */
/* Declarations for MMM model */
double maximum; /* Maximum (children's sim.) */
double minimum; /* Minimum (children's sim.) */
double mmm_sim (); /* Func. computing MMM sim. */
/* Declarations for Paice model */
double child_sims[NUM_ITERMS]; /* Array to store sim. of all
the children of the root */
int curr_i; /* Number of sim. stored in
child_sims */
double paice_sim (); /* Func. computing Paice sim. */
/* Declarations for P-norm model */
double child_wt; /* Wt. of the child */
double numerator; /* Numerator in sim. formula */
double denominator; /* Denominator in sim. formula */
void update_numer_denom(); /* Func. updating value of */
/* numerator & denominator */
double p_norm_sim (); /* Func. computing P-norm sim. */
double calc_tree_sim(); /* Recursive call for each subtree */
/* Addr. of first node of the tree + index of the current node
= the addr. of the root of the subtree under consideration */
root_ptr = query_vec->beg_node_array + root_index;
if UNDEF == root_ptr->child_index)
{/* If node is an index-term, then return its doc-wt. Index in */
/* the doc_wts array is the ITERM_NUM of current index-term */
iterm_ptr = query_vec->beg_iterm_array + root_ptr->iterm_op_index;
doc-index = iterm_ptr->iterm_num;
return ( (double) doc_wts [doc_index] );
}
else
{ /* If current node is an operator, then compute its sim. */op_ptr = query_vec->beg_op_array + root_ptr->iterm_op_index;
if ( ( op_ptr->op_type != NOT_OP ) &&
( op_ptr->op_type != OR_OP ) &&
( op_ptr->op_type != AND_OP ) )
{ /* if neither NOT, OR or AND */fprintf ( stderr, "calc_tree sim:\
illegal operator type %d, query %d.\n",
op_ptr->op_type, query_vec->query_id);
return ( (double) UNDEF );
}
switch (op_ptr->op_type)
{case (NOT_OP): /* If the operator is NOT_OP */
if (UNDEF != (query_vec->beg_node_array +
root_ptr->child_index)->sibling_index)
{ /* NOT_OP operator can have only one child */fprintf(stderr,
"calc_tree_sim: NOT operator has more\
than one child.\n');
return ( (double) UNDEF);
}
/* if only child, return (1.0 - similarity of child) */
if ((double) UNDEF == (child_value =
calc_tree_sim ( doc_wts, query_vec,
root_ptr->child_index, sim_type)))
return ( (double) UNDEF );
return ( 1.0-child_value );
break;
case (OR_OP):
case (AND_OP): /* If the operator is OR_OP or AND_OP */
maximum = -99999.0;
minimum = 99999.0; /* Init. for MMM model */
curr_i = -1; /* Init. for Paice model */
numerator = 0.0;
denominator = 0.0; /* Init. for P-norm model */
/* Start with the first child of the current node, *
* consider each of its siblings, until none left */
for (child_index = root_ptr->child_index;
UNDEF != child_index;
child_index = (query_vec->beg_node_array +
child_index)->sibling_index )
{if ( (double)UNDEF == (child_value =
calc_tree_sim ( doc_wts, query_vec, child_index,
sim_type)))
return ((double UNDEF);
switch (sim_type)
{case (MMM_SIM): /* update max and mim */
maximum = (child_value > maximum) ? child_value
: maximum;
minimum = (child_value < minimum) ? child_value
: minimum;
break;
case (PAICE_SIM):
curr_i = curr_i + 1;
child_sims [curr_i] = child_value;
break;
case (P_NORM_SIM): /* Find the wt. of the child */
child_ptr = query_vec->beg_node_array +
root_ptr->child_index;
if (UNDEF == child_ptr->child_index)
child_wt = (query_vec->beg_iterm_array +
child_ptr->iterm_op_index)->iterm_wt;
else
child_wt = (query_vec->beg_op_array +
child_ptr->iterm_op_index)->op_wt;
update_numer_denom ( child_value, child_wt,
op_ptr->op_type, op_ptr->op_coeff,
&numerator, &denominator );
break;
} /* switch - sim_type */
} /* for */
/* After considering all the children, compute the *
* sim. of current subtree with appropriate formula */
if ( sim_type == MMM_SIM )
return ( mmm_sim ( op_ptr->op_coeff,
op_ptr->op_type, maximum, minimum));
else
if ( sim_type == PAICE_SIM )
return (paice_sim (op_ptr->op_coeff,
op_ptr->op_type, child_sims, curr_i ));
else
if ( sim_type == P_NORM_SIM )
return ( p_norm_sim (op_ptr->op_coeff,
op_ptr->op_type, numerator, denominator ) );
} /* switch - op_ptr->op_type */
} /* else */
}
/***************************************************************************
double
mmm_sim (coeff, type, maximum, minimum)
Returns: The MMM similarity
Purpose: To calculate the MMM similarity using
MAXIMUM and MINIMUM.
SIM(Qor, D) = coeff * MAXIMUM + (1-coeff) * MINIMUM
SIM(Qand, D) = coeff * MINIMUM + (1-coeff) * MAXIMUM
Plan: Depending on the type of the operator use the
appropriate formula
***************************************************************************/
double
mmm_sim ( op_coeff, op_type, maximum, minimum )
register float op_coeff; /* In: Value of the coefficient */
int op_type; /* In: Type of operator */
double maximum; /* In: Maximum of the similarities */
double minimum; /* In: Minimum of the similarities */
{if ( op_type == OR_OP )
return ( (op_coeff * maximum + (1 - op_coeff) * minimum));
else
if ( op_type == AND_OP )
return ( (op_coeff * minimum + (1 - op_coeff) * maximum));
}
/***************************************************************************
double
paice_sim (op_coeff, op_type, child_sims, num_i)
Returns: The Paice similarity
Purpose: To calculate the Paice similarity using the
Paice similarity computation formula
Plan: Sort the array in ascending order
If the operator is OR_OP then:
numerator = SUM (child_sims[i] * op_coeff/\(num_i - i) ) ;
for i = 0 to num_i
denominator = SUM (op_coeff/\(num_i-i));
for i = 0 to num_i
else if the operator is AND_OP then:
numerator = SUM (child_sims[i] *op_coeff/\(i) );
for i = 0 to num_i
denominator = SUM (op_coeff/\(i) );
for i = 0 to num_i
***************************************************************************/
double
paice_sim ( op_coeff, op_type, child_sims, num_i )
register float op_coeff; /* In: Coefficient r */
int op_type; /* In: Type of operator */
double child_sims [NUM_ITERMS]; /* In: Array containing sim. */
int num_i; /* In: No. of elements in
child_sim */
{int i;
double numerator;
double denominator;
double power;
void qsort (); /* Quick Sort Func. in C lib. */
int comp_double (); /* Func. used by qsort */
qsort ( (char *) child_sims, num_i,
sizeof (double), comp_double );
numerator = 0;
denominator = 0;
if ( op_type == OR_OP )
{for (i = 0; i <=num_i; i++)
{power = pow((double) op_coeff, (double)num_i-i);
numerator = numerator + power*child_sims[i];
denominator = denominator + power;
}
return (numerator/denominator);
}
else
if(op_type == AND_OP)
{for (i = 0; i <= num_i; i++)
{power = pow((double) op_coeff, (double)i);
numerator = numerator + power * child_sims[i];
denominator = denominator + power;
}
return ( numerator / denominator );
}
}
/***************************************************************************
int
comp_double ( d1, d2 );
Returns: int
Purpose: Compares d1 and d2 and returns -1, 0, or 1.
***************************************************************************/
int
comp_double (d1, d2)
double *d1, *d2;
{if (*d1 < *d2)
return (-1);
else
if (*d1 == *d2)
return (0);
else
return (1);
}
/***************************************************************************
void
update_numer_denom (value, weight, op_type, p_value,
numerator, denominator)
Returns: Void
Purpose: Update the values of NUMERATOR and DENOMINATOR
Plan: If P_value == P_INFINITY then
if VALUE > NUMERATOR then
NUMERATOR = VALUE
DENOMINATOR = 1
else
if OP_TYPE == OR_OP then
NUMERATOR = NUMERATOR + weight/\P_value * value/\P_value
DENOMINATOR = DENOMINATOR + weight/\P_value
if OP_TYPE == AND_OP then
NUMERATOR = NUMERATOR + weight/\P_value *
(1 - value) /\P_value
DENOMINATOR = DENOMINATOR + weight/\P_value
***************************************************************************/
void
update_numer_denom ( value, weight, op_type, p_value,
numerator, denominator )
double value; /* In: The sim. of the child */
double weight; /* In: The query weight */
register float p_value; /* In: The p_value */
int op_type; /* In: The type of the operator */
register double *numerator; /* Out: Numerator in p-norm sim.
calculation formula */
register double *denominator; /* Out: Denominator in p-norm sim.
calculation formula */
{double power
double pow ()
if (p_value == P_INFINITY)
{*denominator = 1;
if (value > *numerator)
*numerator = value;
}
else
switch (op_type)
{case (OR_OP):
power = pow (weight, p_value);
*numerator = *numerator + power * pow(value,p_value);
*denominator = *denominator + power;
break;
case (AND_OP):
power = pow (weight, p_value );
*numerator = *numerator + power * pow(1-value,p_value);
*denominator = *denominator + power;
break;
}
}
/***************************************************************************
double
p_norm_sim (p_value,op_type,numerator,denominator)
Returns: The P-norm similarity
Purpose: To calculate the P-norm similarity using the
P-norm similarity computation formula
Plan: Depending on the type of the operator use the
appropriate formula
SIM(Q (P_INFINITY) , D) = NUMERATOR
SIM (Qor_P, D) = (NUMERATOR / DENOMINATOR) /\ (1/P)
SIM (Qand_P, D) = 1 - (NUMERATOR / DENOMINATOR) /\ (1/P)
***************************************************************************/
double
p_norm_sim ( p_value, op_type numerator, denominator)
register float p_value; /* In: P value */
int op_type; /* In: Type of operator */
double numerator; /* In: Numerator */
double denominator; /* In: Denominator */
{double pow ();
if (p_value == P_INFINITY)
return (numerator);
else
if (op_type == OR_OP)
return (pow (numerator / denominator, 1/p_value) );
else
if (op_type == AND_OP)
return (1 - pow (numerator / denominator, 1/p_value) );
}


