16.1 CLUSTER ANALYSIS
16.1.1 Introduction
Cluster analysis is a statistical technique used to generate a category structure which fits a set of observations. The groups which are formed should have a high degree of association between members of the same group and a low degree between members of different groups (Anderberg 1973). While cluster analysis is sometimes referred to as automatic classification, this is not strictly accurate since the classes formed are not known prior to processing, as classification implies, but are defined by the items assigned to them.
Because there is no need for the classes to be identified prior to processing, cluster analysis is useful to provide structure in large multivariate data sets. It has been described as a tool of discovery because it has the potential to reveal previously undetected relationships based on complex data (Anderberg 1973). An early application of cluster analysis was to determine taxonomic relationships among species. Psychiatric profiles, medical and clinical data, census and survey data, images, and chemical structures and properties have all been studied using cluster analytic methods, and there is an extensive and widely scattered journal literature on the subject.
Basic texts include those by Anderberg (1973), Hartigan (1975), Everitt (1980), Aldenderfer and Blashfield (1984), Romesburg (1984), Spath (1985), Jain and Dubes (1988) and Kaufman (1990). Taxonomic applications have been described by Sneath and Sokal (1973), and social science applications by Lorr (1983) and Hudson and Associates (1982). Comprehensive reviews by Lee (1981), Dubes and Jain (1980) and Gordon (1987) are also recommended.
Because cluster analysis is a technique for multivariate analysis that has application in many fields, it is supported by a number of software packages which are often available in academic and other computing environments. Most of the methods and some of the algorithms described in this chapter are found in statistical analysis packages such as SAS, SPSSX, and BMDP and cluster analysis packages such as CLUSTAN and CLUSTAR/CLUSTID. Brief descriptions and sources for these and other packages are provided by Romesburg (1984).
The ability of cluster analysis to categorize by assigning items to automatically created groups gives it a natural affinity with the aims of information storage and retrieval. Cluster analysis can be performed on documents in several ways:
Although cluster analysis can be easily implemented with available software packages, it is not without problems. These include:
The emphasis in this chapter will be on the range of clustering methods available and algorithms for their implementation, with discussion of the applications and evaluation that have been carried out in an information retrieval environment. The following notation will be used: N for the numberof items Di in a data set, L for its dimensionality, and M for the number of clusters Ci created. It will be assumed that the items to be clustered are documents, and each document Di (or cluster representative Ci) is represented by (weighti1, . . ., weightiL), where weightik is the weight assigned to termk in Di or Ci. The choice of an appropriate document representation is discussed elsewhere in this text; a summary of research on term-weighting approaches is provided by Salton and Buckley (1988).
In order to cluster the items in a data set, some means of quantifying the degree of association between them is required. This may be a distance measure, or a measure of similarity or dissimilarity. Some clustering methods have a theoretical requirement for use of a specific measure (Euclidean distance for Ward's method, for example), but more commonly the choice of measure is at the discretion of the researcher.
While there are a number of similarity measures available, and the choice of similarity measure can have an effect on the clustering results obtained, there have been only a few comparative studies (summarized by Willett [1988]). In cluster-based retrieval, the determination of interdocument similarity depends on both the document representation, in terms of the weights assigned to the indexing terms characterizing each document, and the similarity coefficient that is chosen. The results of tests by Willett (1983) of similarity coefficients in cluster-based retrieval suggest that it is important to use a measure that is normalized by the length of the document vectors. The results of tests on weighting schemes were less definitive but suggested that weighting of document terms is not as significant in improving performance in cluster-based retrieval as it is in other types of retrieval. Sneath and Sokal (1973) point out that simple similarity coefficients are often monotonic with more complex ones, and argue against the use of weighting schemes. The measures described below are commonly used in information retrieval applications. They are appropriate for binary or real-valued weighting scheme.
A variety of distance and similarity measures is given by Anderberg (1973), while those most suitable for comparing document vectors are discussed by Salton (1989). The Dice, Jaccard and cosine coefficients have the attractions of simplicity and normalization and have often been used for document clustering.
Dice coefficient:
If binary term weights are used, the Dice Coefficient reduces to:
where C is the number of terms that Di and Dj have in common, and A and B are the number of terms in Di and Dj.
Jaccard coefficient:
Cosine coefficient:
Many clustering methods are based on a pairwise coupling of the most similar documents or clusters, so that the similarity between every pair of points must be known. This necessitates the calculation of the similarity matrix; when the similarity measure is symmetric (Sij = Sji), the lower triangular matrix is sufficient (Figure 16.1).
The inverted file algorithm is particularly useful in limiting the amount of computation required to calculate a similarity matrix, if the similarity measure used is one that results in a 0 value whenever a document-document or document-cluster pair have no terms in common (Willett 1980; Perry and Willett 1983). The document term list is used as an index to the inverted index lists that are needed for the similarity calculation. Only those document/cluster pairs that share at least one common term will have their similarity calculated; the remaining values in the similarity matrix are set to 0. The inverted file algorithm is as follows:
The inverted file algorithm can be effectively incorporated in the clustering algorithms described in this chapter when the calculation of the similarity matrix, or a single row of it, is required for a document collection.
It should be noted that the similarity matrix can be the basis for identifying a nearest neighbor (NN), that is, finding the closest vector to a given vector from a set of N multidimensional vectors. The identification of an NN arises in many clustering algorithms, and for large data sets makes a significant contribution to the computational requirement. Calculating and storing the similarity matrix, or recalculating it when needed, provides a brute force approach to nearest neighbor identification. Therefore, if an efficient NN-finding algorithm can be incorporated into the clustering algorithm, considerable savings of processing time may be achieved. However, although there are a number of techniques available for introducing efficiency into the NN-finding process (Bentley et al. 1980; Murtagh 1985), these techniques are generally inappropriate for data sets with the high dimensionality typical of information retrieval applications. Use of the inverted file algorithm to calculate the similarity matrix or a row of it seems to be the best optimization technique available in these circumstances.
There are a very large number of ways of sorting N objects into M groups, a problem compounded by the fact that M is usually unknown. Most of the possible arrangements are of no interest; it is the role of a clustering method to identify a set of groups or cluster that reflects some underlying structure in the data. Moreover, there are many clustering methods available, which have differing theoretical or empirical bases and therefore produce different cluster structures. For a given clustering method, there may be a choice of clustering algorithm or means to implement the method. The choice of clustering method will determine the outcome, the choice of algorithm will determine the efficiency with which it is achieved. In this section, an overview of the clustering methods most used in information retrieval will be provided. The associated algorithms that are best suited to the processing of the large data sets found in information retrieval applications are discussed in sections 16.4 and 16.5.
In cases where the data set to be processed is very large, the resources required for cluster analysis may be considerable. A major component of the computation required is the calculation of the document-document or document-cluster similarity. The time requirement will be minimally O(NM), where M is the number of clusters, for the simpler reallocation methods; where the similarity matrix must be constructed, the proportionality is at least N2. Most of the preferred clustering methods have time requirements of at least O(N2). The storage requirement will be O(N) if the data set is stored, or O(N2) if the similarity matrix is stored. For large N this may be unacceptable, and disk accesses may make processing time too large if the similarity matrix is stored on disk. An alternative is to recalculate the similarity matrix from the stored data whenever it is needed to identify the current most similar pair, but this increases the time requirement by a factor of N2.
Because of the heavy demands of processing and storage requirements, much of the early work on cluster analysis for information retrieval was limited to small data sets, often only a few hundred items. However, improvements in processing and storage capacity and the introduction of efficient algorithms for implementing some clustering methods and finding nearest neighbors have made it feasible to cluster increasingly large data sets. Salton and Bergmark (1981) have pointed out that there is a high degree of parallelism in the calculation of a set of similarity values, and parallel hardware also offers the potential for increased processing efficiency (Willett and Rasmussen 1990).
Clustering methods are usually categorized according to the type of cluster structure they produce. The simple nonhierarchical methods divide the data set of N objects into M clusters; where no overlap is allowed, these are known as partitioning methods. Each item has membership in the cluster with which it is most similar, and the cluster may be represented by a centroid or cluster representative that is indicative of the characteristics of the items it contains. The more complex hierarchical methods produce a nested data set in which pairs of items or clusters are successively linked until every item in the data set is connected. The hierarchical methods can be either agglomerative, with N - 1 pairwise joins beginning from an unclustered data set, or divisive, beginning with all objects in a single cluster and progressing through N - 1 divisions of some cluster into a smaller cluster. The divisive methods are less commonly used and few algorithms are available; only agglomerative methods will be discussed in this chapter.
The nonhierarchical methods are heuristic in nature, since a priori decisions about the number of clusters, cluster size, criterion for cluster membership, and form of cluster representation are required. Since the large number of possible divisions of N items into M clusters make an optimal solution impossible, the nonhierarchical methods attempt to find an approximation, usually by partitioning the data set in some way and then reallocating items until some criterion is optimized. The computational requirement O(NM) is much lower than for the hierarchical methods if M << N, so that large data sets can be partitioned. The nonhierarchical methods were used for most of the early work in document clustering when computational resources were limited; see for example work on the SMART project, described by Salton (1971).
Most of the early published work on cluster analysis employed hierarchical methods (Blashfield and Aldenderfer 1978), though this was not so in the IR field. With improvements in computer resources, the easy availability of software packages for cluster analysis, and improved algorithms, the last decade of work on clustering in IR retrieval has concentrated on the hierarchical agglomerative clustering methods (HACM, Willett [1988]).
The cluster structure resulting from a hierarchical agglomerative clustering method is often displayed as a dendrogram like that shown in Figure 16.2. The order of pairwise coupling of the objects in the data set is shown, and the value of the similarity function (level) at which each fusion occurred. The dendrogram is a useful representation when considering retrieval from a clustered set of documents, since it indicates the paths that the retrieval process may follow.
The most commonly used hierarchical agglomerative clustering methods and their characteristics are:
Two other HACM are sometimes used, the centroid and median methods. In the centroid method, each cluster as it is formed is represented by the coordinates of a group centroid, and at each stage in the clustering the pair of clusters with the most similar mean centroid is merged. The median method is similar but the centroids of the two merging clusters are not weighted proportionally to the size of the clusters. A disadvantage of these two methods is that a newly formed cluster may be more like some point than were its constituent points, resulting in reversals or inversions in the cluster hierarchy.
The single pass method is particularly simple since it requires that the data set be processed only once. The general algorithm is as follows:
1. Assign the first document D1 as the representative for C1.
2. For Di, calculate the similarity S with the representative for each existing cluster.
3. If Smax is greater than a threshold value ST, add the item to the corresponding cluster and recalculate the cluster representative; otherwise, use Di to initiate a new cluster.
4. If an item Di remains to be clustered, return to step 2.
Though the single pass method has the advantage of simplicity, it is often criticized for its tendency to produce large clusters early in the clustering pass, and because the clusters formed are not independent of the order in which the data set is processed. It is sometimes used to form the groups that are used to initiate reallocation clustering. An example of a single pass algorithm developed for document clustering is the cover coefficient algorithm (Can and Ozkarahan 1984). In this algorithm, a set of documents is selected as cluster seeds, and then each document is assigned to the cluster seed that maximally covers it. For Di, the cover coefficient is a measure that incorporates the extent to which it is covered by Dj and the uniqueness of Di, that is, the extent to which it is covered by itself.
The reallocation methods operate by selecting some initial partition of the data set and then moving items from cluster to cluster to obtain an improved partition. Anderberg (1973) discusses some of the criteria that have been suggested to establish an initial partition and to monitor the improvement achieved by reallocation. A general algorithm is:
1. Select M cluster representatives or centroids.
2. For i = 1 to N, assign Di to the most similar centroid.
3. For j = 1 to M, recalculate the cluster centroid Cj.
4. Repeat steps 2 and 3 until there is little or no change in cluster membership during a pass through the file.
The single pass and reallocation methods were used in early work in cluster analysis in IR, such as the clustering experiments carried out in the SMART project (Salton 1971). Their time and storage requirements are much lower than those of the HACM and much larger data sets could be processed. With improved processing capability and more efficient hierarchical algorithms, the HACMs are now usually preferred in practice, and the nonhierarchical methods will not be considered further in this chapter.
All of the hierarchical agglomerative clustering methods can be described by a general algorithm:
1. Identify the two closest points and combine them in a cluster.
2. Identify and combine the next two closest points (treating existing clusters as points).
3. If more than one cluster remains, return to step 1.
Individual HACM differ in the way in which the most similar pair is defined, and in the means used to represent a cluster. Lance and Williams (1966) proposed a general combinatorial formula, the Lance-Williams dissimilarity update formula, for calculating dissimilarities between new clusters and existing points, based on the dissimilarities prior to formation of the new cluster. If objects Ci and Cj have just been merged to form cluster Cij, the dissimilarity d between the new cluster and any existing cluster Ck is given by:
dCi,jck =
This formula can be modified to accomodate a variety of HACM by choice of the values of
There are three approaches to implementation of the general HACM (Anderberg 1973), each of which has implications for the time and storage requirements for processing. In the stored matrix approach, an N
In addition to the general algorithm, there are also algorithms specific to individual HACM. For some methods, algorithms have been developed that are the optimal O (N2) in time and O (N) in space (Murtagh 1984). These include several algorithms for the single link method, Defay's algorithm for complete link, and a nearest-neighbor algorithm for Ward's method, all of which are discussed below.
The single link method merges at each stage the closest previously unlinked pair of points in the data set. Since the distance between two clusters is defined as the distance between the closest pair of points each of which is in one of the two clusters, no cluster centroid or representative is required, and there is no need to recalculate the similarity matrix during processing. This makes the method attractive both from a computational and a storage perspective, and it also has desirable mathematical properties (Jardine and Sibson 1971), so that it is one of the most widely used of the HACM.
A number of algorithms for the single link method have been reviewed by Rohlf (1982), including related minimal spanning tree algorithms. The computational requirements range from O (NlogN) to O (N5). Many of these algorithms are not suitable for information retrieval applications where the data sets have large N and high dimensionality. The single link algorithms discussed below are those that have been found most useful for information retrieval.
Van Rijsbergen (1971) developed an algorithm to generate the single link hierarchy that allowed the similarity values to be presented in any order and therefore did not require the storage of the similarity matrix. It is O (N2) in time and O (N) in storage requirements. It generates the hierarchy in the form of a data structure that both facilitates searching and is easily updated, and was the first to be applied to a relatively large collection of 11,613 documents (Croft 1977). However, most later work with large collections has used either the SLINK or Prim-Dijkstra algorithm, which are quite simple to implement.
The SLINK algorithm (Sibson 1973) is optimally efficient, O (N2) for computation and O (N) for time, and therefore suitable for large data sets. It is simply a sequence of operations by which a representation of the single link hierarchy can be recursively updated; the dendrogram is built by inserting one point at a time into the representation.
The hierarchy is generated in a form known as the pointer representation, which consists of two functions
In simple terms,
Fortran code for SLINK is provided in the original paper (Sibson 1973). In the pseudocode below, three arrays of dimension N are used: pi (to hold the pointer representation), lambda (to hold the distance value associated with each pointer), and distance (to process the current row of the distance matrix); next indicates the current pointer for a point being examined.
For output in the form of a dendrogram, the pointer representation can be converted into the packed representation. This can be accomplished in O (N2) time (with a small coefficient for N2) and O (N) space. A FORTRAN subroutine to effect the transformation is provided in Sibson's original paper.
A minimal spanning tree (MST) is a tree linking N objects with N - 1 connections so that there are no loops and the sum of the N - 1 dissimilarities is minimized. It can be shown that all the information required to generate a single link hierarchy for a set of points is contained in their MST (Gower and Ross 1969). Once an MST has been constructed, the corresponding single link hierarchy can be generated in O (N2) operations; or the data structures for the MST can be modified so that the hierarchy can be built simultaneously (Rohlf 1982).
Two fundamental construction principles for MSTs are:
1. Any isolated point can be connected to a nearest neighbor.
2. Any isolated fragment (subset of an MST) can be connected to a nearest neighbor by a shortest available link.
The Prim-Dijkstra algorithm (Dijkstra 1976) consists of a single application of principle 1, followed by N - 1 iterations of principle 2, so that the MST is grown by enlarging a single fragment:
1. Place an arbitrary point in the MST and connect its nearest neighbor to it.
2. Find the point not in the MST closest to any point in the MST and add it to the fragment.
3. If a point remains that is not in the fragment, return to step 2.
The algorithm requires O (N2) time if, for each point not in the fragment, the identity and distance to its nearest neighbor in the fragment is stored. As each new point is added to the fragment, the distance from that point to each point not in the fragment is calculated, and the NN information is updated if necessary. Since the dissimilarity matrix need not be stored, the storage requirement is O (N).
A FORTRAN version of the Prim-Dijkstra algorithm is provided by Whitney (1972). The algorithm here uses arrays npoint and ndistance to hold information on the nearest in-tree neighbor for each point, and notintree is a list of the nt unconnected points. Lastpoint is the latest point added to the tree.
The small, tightly bound clusters typical of the complete link method have performed well in comparative studies of document retrieval (Voorhees 1986a). Unfortunately, it is difficult to apply to large data sets since there does not seem to be an algorithm more effective than the stored data or stored matrix approach to the general HACM algorithm.
The best-known algorithm for implementing the complete link method is the CLINK algorithm developed by Defays (1977). It is presented in a form analogous to the SLINK algorithm, uses the same three arrays (pi, lambda, and distance), and like SLINK, produces output in the form of the pointer representation. Defays presents a CLINK subroutine which allows his algorithm to be incorporated into Sibson's original FORTRAN program for SLINK. CLINK is efficient, requiring O (N2) time, O (N) space, but it does not seem to generate an exact hierarchy and has given unsatisfactory results in some information retrieval experiments (El-Hamdouchi and Willett 1989).
The Voorhees algorithm (1986b) for the complete link method has been used to cluster relatively large document collections with better retrieval results than the CLINK algorithm (El-Hamdouchi and Willett 1989). It is a variation on the sorted matrix approach, and is based on the fact that if the similarities between all pairs of documents are processed in descending order, two clusters of size mi and mj can be merged as soon as the mi
Because the similarity between two clusters is determined by the average value of all the pairwise links between points for which each is in one of the two clusters, no general O (N2) time, O (N) space algorithm is known. The general HACM algorithm can be used, but with O (N3) time for the stored data approach and O (N2) storage for the stored matrix approach, implementation may be impractical for a large collection. However, a more efficient special case algorithm is available.
Voorhees (1986b) has pointed out that the group average link hierarchy can be constructed in O (N2) time, O (N) space if the similarity between documents chosen is the inner product of two vectors using appropriately weighted vectors. In this case, the similarity between a cluster centroid and any document is equal to the mean similarity between the document and all the documents in the cluster. Since the centroid of the cluster is the mean of all the document vectors, the centroids can be used to compute the similarities between the clusters while requiring only O(N) space. Voorhees was able to cluster a document collection of 12,684 items using this algorithm, for which she provides pseudocode.
Using Voorhees' weighting scheme and intercentroid similarity, El-Hamdouchi (1987) was able to implement the group average link method using the reciprocal nearest neighbor algorithm described below for Ward's method.
Ward's method (Ward 1963; Ward and Hook 1963) follows the general algorithm for the HACM, where the object/cluster pair joined at each stage is the one whose merger minimizes the increase in the total within-group squared deviation about the means, or variance. When two points Di and Dj are clustered, the increase in variance Iij is given by:
where mi is the number of objects in Di and d2ij is the squared Euclidean distance, given by:
where Di is represented by a vector (xi1, xi2, . . . , xiL) in L-dimensional space. The cluster center for a pair of points Di and Dj is given by:
The mathematical properties of Ward's method make it a suitable candidate for a reciprocal nearest neighbor (RNN) algorithm (Murtaugh 1983, 1985). For any point or cluster, there exists a chain of nearest neighbors (NNs) so that
The chain must end in some pair of objects that are RNNs, since the interobject distances are monotonically decreasing along the chain (ties must be arbitrarily resolved).
An efficient clustering algorithm can be based on the process of following a chain of nearest neighbors:
1. Select an arbitrary point.
2. Follow the NN chain from this point till an RNN pair is found.
3. Merge these two points and replace them with a single point.
4. If there is a point in the NN chain preceding the merged points, return to step 2; otherwise return to step 1. Stop when only one point remains.
This algorithm requires O(N2) computation but only O(N) storage. It carries out agglomerations in restricted spatial regions, rather than in strict order of increasing dissimilarity, but still results (for Ward's method) in a hierarchy that is unique and exact. This is designated the Single Cluster Algorithm since it carries out one agglomeration per iteration; a Multiple Cluster Algorithm, suitable for parallel processing, has also been proposed (Murtagh 1985).
As Dubes and Jain (1980, p. 179) point out:
The thoughtful user of a clustering method or algorithm must answer two questions: (i) Which clustering method is appropriate for a particular data set? (ii) How does one determine whether the results of a clustering method truly characterize the data?
These are important questions because any clustering method will produce a set of clusters, and results are sought which reflect some "natural" grouping rather than one that arises as an artifact of the method. The answer to the first question can be found in evaluative studies of clustering methods, and to the second question, in validation techniques for clustering solutions.
Many evaluative studies have attempted to determine the "best" clustering method (Lorr 1983) by applying a range of clustering methods to test data sets and comparing the quality of the results, for example by using artificially created data structures, or comparing the cluster results to a classification established by experts in the field. Even under laboratory conditions it is difficult to evaluate clustering methods, since each method has different properties and strengths. The results of these studies do not suggest a single best method, though Ward's method, and in more recent studies, the group average method, have performed well. It is usually advisable to apply more than one clustering method and use some validation method to check the reliability of the resulting cluster structure.
For retrieval purposes, the "best" method for clustering a document collection is that which provides the most effective retrieval in response to a query. Several evaluative studies have taken this approach, using standard test collections of documents and queries. Most of the early work used approximate clustering methods, or the least demanding of the HACM, the single link method, a restriction imposed by limited processing resources. However, two recent studies are noteworthy for their use of relatively large document collections for the evaluation of a variety of HACM (El-Hamdouchi and Willett 1989; Voorhees 1986a). Voorhees compared single link, complete link, and group average methods, using document collections of up to 12,684 items, while El-Hamdouchi and Willett compared these three methods plus Ward's method on document collections of up to 27,361 items. Voorhees found complete link most effective for larger collections, with complete and group average link comparable for smaller collections; single link hierarchies provided the worst retrieval performance. El-Hamdouchi and Willett found group average most suitable for document clustering. Complete link was not as effective as in the Voorhees study, though this may be attributed to use of Defays' CLINK algorithm. As noted in section 16.8.1, there are several ways in which retrieval from a clustered document collection can be performed, making comparisons difficult when using retrieval as an evaluative tool for clustering methods.
Cluster validity procedures are used to verify whether the data structure produced by the clustering method can be used to provide statistical evidence of the phenomenon under study. Dubes and Jain (1980) survey the approaches that have been used, categorizing them on their ability to answer four questions: is the data matrix random? how well does a hierarchy fit a proximity matrix? is a partition valid? and which individual clusters appearing in a hierarchy are valid? Willett (1988) has reviewed the application of validation methods to clustering of document collections, primarily the application of the random graph hypothesis and the use of distortion measures.
An approach that is carried out prior to clustering is also potentially useful. Tests for clustering tendency attempt to determine whether worthwhile retrieval performance would be achieved by clustering a data set, before investing the computational resources which clustering the data set would entail. El-Hamdouchi and Willett (1987) describe three such tests. The overlap test is applied to a set of documents for which query-relevance judgments are available. All the relevant-relevant (RR) and relevant-nonrelevant (RNR) interdocument similarities are calculated for a given query, and the overlap (the fraction of the RR and RNR distributions that is common to both) is calculated. Collections with a low overlap value are expected to be better suited to clustering than those with high overlap values. Voorhees' nearest neighbor test considers, for each relevant document for a query, how many of its n nearest neighbors are also relevant; by averaging over all relevant documents for all queries in a test colleciton, a single indicator for a collection can be obtained. The density test is defined as the total number of postings in the document collection divided by the product of the number of documents and the number of terms that have been used for the indexing of those documents. It is particularly useful because it does not require any predetermined query-relevance data or any calculation of interdocument similarities. Of the three tests, the density test provided the best indication of actual retrieval performance from a clustered data set.
The goal of a hierarchical clustering process may be to partition the data set into some unknown number of clusters M (which may be visualized as drawing a horizontal line across the dendrogram at some clustering level). This requires the application of a stopping rule, a statistical test to predict the clustering level that will determine M. Milligan and Cooper (1985) evaluated and ranked 30 such rules, one or more of which is usually present in a software package for cluster analysis (though not necessarily those ranked highest by Milligan and Cooper).
In many information retrieval environments, the collection is dynamic, with new items being added on a regular basis, and, less frequently, old items withdrawn. Since clustering a large data set is resource-intensive, some mechanism for updating the cluster structure without the need to recluster the entire collection is desirable. Relatively little work has been done on methods for cluster maintenance (Can and Ozkarahan 1989), particularly for the hierarchical methods. In certain cases, update of the cluster structure is implicit in the clustering algorithm. This is true of both the van Rijsbergen and SLINK algorithms for the single link method, and the CLINK algorithm for the complete link method, all of which operate by iteratively inserting a document into an existing hierarchy.
Where the application uses a partitioned data set (from a nonhierarchical or hierarchical method), new items may simply be added to the most similar partition until the cluster structure becomes distorted and it is necessary to regenerate it. For a few methods, cluster update has been specifically incorporated. Crouch's reallocation algorithm includes a mechanism for cluster maintenance (Crouch 1975). Can and Ozkarahan (1989) review the approaches that have been taken for cluster maintenance and propose a strategy for dynamic cluster maintenance based on their cover coefficient concept.
Document clustering has been studied because of its potential for improving the efficiency of retrieval, for improving the effectiveness of retrieval, and because it provides an alternative to Boolean or best match retrieval. Initially the emphasis was on efficiency: document collections were partitioned, using nonhierarchical methods, and queries were matched against cluster centroids, which reduced the number of query-document comparisons that were necessary in a serial search. Studies of retrieval from partitioned document collections showed that though retrieval efficiency was achieved, there was a decrease in retrieval effectiveness (Salton 1971). Subsequent study has concentrated on the effectiveness of retrieval from hierarchically clustered document collections, based on the cluster hypothesis, which states that associations between documents convey information about the relevance of documents to requests (van Rijsbergen 1979).
There are several ways in which a query can be matched against the documents in a hierarchy (Willett 1988). A top-down search involves entering the tree at the root and matching the query against the cluster at each node, moving down the tree following the path of greater similarity. The search is terminated according to some criterion, for instance when the cluster size drops below the number of documents desired, or when the query-cluster similarity begins to decrease. A single cluster is retrieved when the search is terminated. Since it is difficult to adequately represent the clusters in the very large top-level clusters, a useful modification is to eliminate the top-level clusters by applying a threshold clustering level to the hierarchy to obtain a partition, and using the best of these mid-level clusters as the starting point for the top-down search. The top-down strategy has been shown to work well with the complete link method (Voorhees 1986a).
A bottom-up search begins with some document or cluster at the base of the tree and moves up until the retrieval criterion is satisfied; the beginning document may be an item known to be relevant prior to the search, or it can be obtained by a best match search of documents or lowest-level clusters. Comparative studies suggest that the bottom-up search gives the best results (apart from the complete link method), particularly when the search is limited to the bottom-level clusters (Willett 1988). Output may be based on retrieval of a single cluster, or the top-ranking clusters may be retrieved to produce a predetermined number of either documents or clusters; in the latter case, the documents retrieved may themselves be ranked against the query.
A simple retrieval mechanism is based on nearest neighbor clusters, that is, retrieving a document and that document most similar to it. Griffiths et al. (1984) determined that for a variety of test collections, search performance comparable to or better than that obtainable from nonclustered collections could be obtained using this method.
A centroid or cluster representative is a record that is used to represent the characteristics of the documents in a cluster. It is required in retrieval so that the degree of similarity between a query and a cluster can be determined; it is also needed in the nonhierarchical methods where document-cluster similarity must be determined in order to add documents to the most similar cluster. Ranks or frequencies have been used to weight terms in the representative; usually a threshold is applied to eliminate less significant terms and shorten the cluster representative. A binary representative may also be used, for example including a term if it occurs in more than log2m documents in the cluster (Jardine and van Rijsbergen 1971).
Cluster analysis is an effective technique for structuring a data set, and a wide choice of methods and algorithms exists. It is important to consider the questions raised in section 16.1.2 regarding the potential application, selection of methods and algorithm and the parameters associated with it, and evaluation and validation of the results. Much of the work to date in cluster analysis has been limited by the considerable resources required by clustering, and only recently have results from relatively large-scale clustering become available.
ALDENDERFER, M. S., and R. K. BLASHFIELD. 1984. Cluster Analysis. Beverly Hills: Sage.
ANDERBERG, M. R., 1973. Cluster Analysis for Applications. New York: Academic.
BENTLEY, J. L., B. W. WEIDE, and A. C. YAO. 1980. "Optimal Expected-Time Algorithms for Closest Point Problems." ACM Transactions on Mathematical Software, 6, 563-80.
BLASHFIELD, R. K., and M. S. ALDENDERFER. 1978. "The Literature on Cluster Analysis." Multivariate Behavioral Research, 13, 271-95.
CAN, F., and E. A. OZKARAHAN. 1984. "Two Partitioning Type Clustering Algorithms." J. American Society for Information Science, 35, 268-76.
CAN, F., and E. A. OZKARAHAN. 1989. "Dynamic Cluster Maintenance." Information Processing & Management, 25, 275-91.
CROFT, W. B. 1977. "Clustering Large Files of Documents Using the Single-Link Method." J. American Society for Information Science, 28, 341-44.
CROUCH, C. J. 1988. "A Cluster-Based Approach to Thesaurus Construction" in 11th International Conference on Research and Development in Information Retrieval, New York: ACM, 309-20.
CROUCH, D. B. 1975. "A File Organization and Maintenance Procedure for Dynamic Document Collections." Information Processing & Management, 11, 11-21.
DEFAYS, D. 1977. "AEfficient n Algorithm for a Complete Link Method." Computer Journal, 20, 364-66.
DIJKSTRA, E. W. 1976. "The Problem of the Shortest Subspanning Tree." A Discipline of Programming. Englewood Cliffs, N.J.: Prentice Hall, 154-60.
DUBES, R., and A. K. JAIN. 1980. "Clustering Methodologies in Exploratory Data Analysis." Advances in Computers, 19, 113-227.
EL-HAMDOUCHI, A. 1987. The Use of Inter-Document Relationships in Information Retrieval. Ph.D. thesis, University of Sherfield.
EL-HAMDOUCHI, A., and P. WILLETT. 1987. "Techniques for the Measurement of Clustering Tendency in Document Retrieval Systems." J. Information Science, 13, 361-65.
EL-HAMDOUCHI, A., and P. WILLETT. 1989. "Comparison of hierarchic agglomerative clustering methods for document retrieval." Computer Journal, 32, 220-227.
EVERITT, B. 1980. Cluster Analysis, 2nd ed. New York: Halsted.
GORDON, A. D. 1987. "A Review of Hierarchical Classification." J. Royal Statistical Society, Series A, 150(2), 119-37.
GOWER, J. C., and G. J. S. ROSS. 1969. "Minimum Spanning Trees and Single Linkage Cluster Analysis." Applied Statistics, 18, 54-64.
GRIFFITHS, A., L . A. ROBINSON, and P. WILLETT. 1984. "Hierarchic Agglomerative Clustering Methods for Automatic Document Classification." J. Documentation, 40, 175-205.
HARTIGAN, J. A. 1975. Clustering Algorithms. New York: Wiley.
HUDSON, H. C., and ASSOCIATES. 1983. Classifying Social Data: New Applications of Analytical Methods for Social Science Research. San Francisco: Jossey-Bass.
JAIN, A. K., and R. C. DUBES. 1988. Algorithms for Clustering Data. Englewood Cliffs, N.J.: Prentice Hall.
JARDINE, N., and R. SIBSON. 1971. Mathematical Taxonomy. London: Wiley.
JARDINE, N., and C. J. VAN RIJSBERGEN. 1971. "The Use of Hierarchic Clustering in Information Retrieval." Information Storage and Retrieval, 7, 217-40.
KAUFMAN, L. 1990. Finding Groups in Data: An Introduction to Cluster Analysis. New York: Wiley.
LANCE, G. N., and W. T. WILLIAMS. 1966. "A General Theory of Classificatory Sorting Strategies. 1 . Hierarchical systems." Computer Journal, 9, 373-80.
LEE, R. C. T. 1981. "Clustering Analysis and Its Applications." Advances in Information Systems Science, 8, 169-292.
LORR, M. 1983. Cluster Analysis for Social Scientists: Techniques for Analyzing and Simplifying Complex Blocks of Data. San Francisco: Jossey-Bass.
MILLIGAN, G. W., and M. C. COOPER. 1985. "An Examination of Procedures for Determining the Number of Clusters in a Data Set." Psychometrika, 50, 159-79.
MURTAGH, F. 1983. "A Survey of Recent Advances in Hierarchical Clustering Algorithms." Computer Journal, 26, 354-59.
MURTAGH, F. 1984. "Complexities of Hierarchic Clustering Algorithms: State of the Art." Computational Statistics Quarterly, 1, 101-13.
MURTAGH, F. 1985. Multidimensional Clustering Algorithms. Vienna: Physica-Verlag (COMP-STAT Lectures 4).
PERRY, S. A., and P. WILLETT. 1983. "A Review of the Use of Inverted Files for Best Match Searching in Information Retrieval Systems." J. Information Science, 6, 59-66.
ROHLF, F. J. 1982. "Single-Link Clustering Algorithms," Classification, Pattern Recognition, and Reduction of Dimensionality, eds. P. R. Krishnaiah and J. N. Kanal, pp. 267-84. Amsterdam: North-Holland (Handbook of Statistics, Vol. 2).
ROMESBURG, H. C. 1984. Cluster Analysis for Researchers. Belmont, Calif.: Lifetime Learning.
SALTON, G., ed. 1971. The SMART Retrieval System. Englewood Cliffs, N.J.: Prentice Hall.
SALTON, G. 1989. Automatic Text Processing. Reading, Mass.: Addison-Wesley.
SALTON, G., and D. BERGMARK. 1981. "Parallel Computations in Information Retrieval." Lecture Notes in Computer Science, 111, 328-42.
SALTON, G., and C. BUCKLEY. 1988. "Term-Weighting Approaches in Automatic Text Retrieval." Information Processing & Management, 24, 513-23.
SIBSON, R. 1973. "SLINK: an Optimally Efficient Algorithm for the Single-Link Cluster Method." Computer Journal, 16, 30-34.
SMALL, H., and E. SWEENEY. 1985. "Clustering the Science Citation Index Using Co-citations. I. A Comparison of Methods." Scientometrics, 7, 391-409.
SNEATH, P. H. A., and R. R. Sokal. 1973. Numerical Taxonomy; the Principles and Practice of Numerical Classification. San Francisco: W. H. Freeman.
SPATH, H. 1985. Cluster Dissection and Analysis. Chichester: Ellis Horwood.
VAN RIJSBERGEN, C. J. 1971. "An Algorithm for Information Structuring and Retrieval." Computer Journal, 14, 407-12.
VAN RIJSBERGEN, C. J. 1979. Information Retrieval. London: Butterworths.
VOORHEES, E. M. 1986a. The Effectiveness and Efficiency of Agglomerative Hierarchic Clustering in Document Retrieval. Ph.D. thesis, Cornell University.
VOORHEES, E. M. 1986b. "Implementing Agglomerative Hierarchic Clustering Algorithms for Use in Document Retrieval. Information Processing & Management, 22, 465-76.
WARD, J. H., JR. 1963. "Hierarchical Grouping to Optimize an Objective Function. J. American Statistical Association, 58(301), 235-44.
WARD, J. H., JR. and M. E. HOOK. 1963. "Application of an Hierarchical Grouping Procedure to a Problem of Grouping Profiles." Educational and Psychological Measurement, 23, 69-81.
WHITNEY, V. K. M. 1972. "Algorithm 422: Minimal Spanning Tree." Communications of the ACM, 15, 273-74.
WILLETT, P. 1980. "Document Clustering Using an Inverted File Approach." J. Information Science, 2, 223-31.
WILLETT, P. 1983. "Similarity Coefficients and Weighting Functions for Automatic Document Classification: an Empirical Comparison." International Classification, 10, 138-42.
WILLETT, P. 1988. "Recent Trends in Hierarchic Document Clustering: A Critical Review." Information Processing & Management, 24(5), 577-97.
WILLETT, P., and E. M. RASMUSSEN. 1990. Parallel Database Processing. London: Pitman (Research Monographs in Parallel and Distributed Computing).
16.1.2 Applications in Information Retrieval
 Documents may be clustered on the basis of the terms that they contain. The aim of this approach has usually been to provide more efficient or more effective retrieval, though it has also been used after retrieval to provide structure to large sets of retrieved documents. In distributed systems, clustering can be used to allocate documents for storage. A recent review (Willett 1988) provides a comprehensive summary of research on term-based document clustering.
Documents may be clustered on the basis of the terms that they contain. The aim of this approach has usually been to provide more efficient or more effective retrieval, though it has also been used after retrieval to provide structure to large sets of retrieved documents. In distributed systems, clustering can be used to allocate documents for storage. A recent review (Willett 1988) provides a comprehensive summary of research on term-based document clustering. Documents may be clustered based on co-occurring citations in order to provide insights into the nature of the literature of a field (e.g., Small and Sweeney [1985]).
Documents may be clustered based on co-occurring citations in order to provide insights into the nature of the literature of a field (e.g., Small and Sweeney [1985]). Terms may be clustered on the basis of the documents in which they co-occur, in order to aid in the construction of a thesaurus or in the enhancement of queries (e.g., Crouch [1988]).
Terms may be clustered on the basis of the documents in which they co-occur, in order to aid in the construction of a thesaurus or in the enhancement of queries (e.g., Crouch [1988]). Selecting the attributes on which items are to be clustered and their representation.
Selecting the attributes on which items are to be clustered and their representation. Selecting an appropriate clustering method and similarity measure from those available .
Selecting an appropriate clustering method and similarity measure from those available . Creating the clusters or cluster hierarchies, which can be expensive in terms of computational resources.
Creating the clusters or cluster hierarchies, which can be expensive in terms of computational resources. Asessing the validity of the result obtained.
Asessing the validity of the result obtained. If the collection to be clustered is a dynamic one, the requirements for update must be considered.
If the collection to be clustered is a dynamic one, the requirements for update must be considered. If the aim is to use the clustered collection as the basis for information retrieval, a method for searching the clusters or cluster hierarchy must be selected.
If the aim is to use the clustered collection as the basis for information retrieval, a method for searching the clusters or cluster hierarchy must be selected.16.2 MEASURES OF ASSOCIATION
16.2.1 Introduction
16.2.2 Similarity Measures
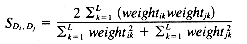
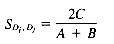
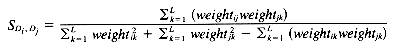

16.2.3 The Similarity Matrix

Figure 16.1: Similarity matrix
for ( docno = 0; docno < n; docno++ )
{for ( i = 0; i < doclength; i++ )
{retrieve_inverted_list ( term[i] );
for ( j = 0; j < invlength; j++ ) counter[doc[j]]++;
}
for ( doc2 = 0; doc2 < n; doc2++ )
{if (counter [doc2]) calc_similarity( docno, doc2 );
}
}
16.3 CLUSTERING METHOS
16.3.1 Methods and Associated Algorithms
16.3.2 Computational and Storage Requirements
16.3.3 Survey of Clustering Methods
Nonhierarchical methods
Hierarchical methods
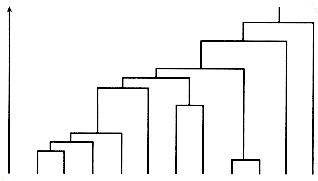
Figure 16.2: Dendrogram of a hierarchical classification
 single link: The single link method joins, at each step, the most similar pair of objects that are not yet in the same cluster. It has some attractive theoretical properties (Jardine and Sibson 1971) and can be implemented relatively efficiently, so it has been widely used. However, it has a tendency toward formation of long straggly clusters, or chaining, which makes it suitable for delineating ellipsoidal clusters but unsuitable for isolating spherical or poorly separated clusters.
single link: The single link method joins, at each step, the most similar pair of objects that are not yet in the same cluster. It has some attractive theoretical properties (Jardine and Sibson 1971) and can be implemented relatively efficiently, so it has been widely used. However, it has a tendency toward formation of long straggly clusters, or chaining, which makes it suitable for delineating ellipsoidal clusters but unsuitable for isolating spherical or poorly separated clusters. complete link: The complete link method uses the least similar pair between each of two clusters to determine the intercluster similarity; it is called complete link because all entities in a cluster are linked to one another within some minimum similarity. Small, tightly bound clusters are characteristic of this method.
complete link: The complete link method uses the least similar pair between each of two clusters to determine the intercluster similarity; it is called complete link because all entities in a cluster are linked to one another within some minimum similarity. Small, tightly bound clusters are characteristic of this method. group average link: As the name implies, the group average link method uses the average values of the pairwise links within a cluster to determine similarity. All objects contribute to intercluster similarity, resulting in a structure intermediate between the loosely bound single link clusters and tightly bound complete link clusters. The group average method has ranked well in evaluative studies of clustering methods (Lorr 1983).
group average link: As the name implies, the group average link method uses the average values of the pairwise links within a cluster to determine similarity. All objects contribute to intercluster similarity, resulting in a structure intermediate between the loosely bound single link clusters and tightly bound complete link clusters. The group average method has ranked well in evaluative studies of clustering methods (Lorr 1983). Ward's method: Ward's method is also known as the minimum variance method because it joins at each stage the cluster pair whose merger minimizes the increase in the total within-group error sum of squares, based on the Euclidean distance between centroids. It tends to produce homogeneous clusters and a symmetric hierarchy, and its definition of a cluster center of gravity provides a useful way of representing a cluster. Tests have shown it to be good at recovering cluster structure, though it is sensitive to outliers and poor at recovering elongated clusters (Lorr 1983).
Ward's method: Ward's method is also known as the minimum variance method because it joins at each stage the cluster pair whose merger minimizes the increase in the total within-group error sum of squares, based on the Euclidean distance between centroids. It tends to produce homogeneous clusters and a symmetric hierarchy, and its definition of a cluster center of gravity provides a useful way of representing a cluster. Tests have shown it to be good at recovering cluster structure, though it is sensitive to outliers and poor at recovering elongated clusters (Lorr 1983).16.4 ALGORITHMS FOR NONHIERARCHICAL METHODS
16.4.1 Single Pass Methods
16.4.2 Reallocation Methods
16.5 ALGORITHMS FOR HIERARCHICAL METHODS
16.5.1 General Algorithm for the HACM
 idcick + ajdcjck +
idcick + ajdcjck +  dcicj +
dcicj + 
 dcick - dcjck
dcick - dcjck
 ,
,  , and
, and  . The hierarchical clustering methods previously discussed are presented in Table 16.1 in the context of their Lance-Williams parameters and cluster centers.
. The hierarchical clustering methods previously discussed are presented in Table 16.1 in the context of their Lance-Williams parameters and cluster centers.Table 16.1: Characteristics of HACM
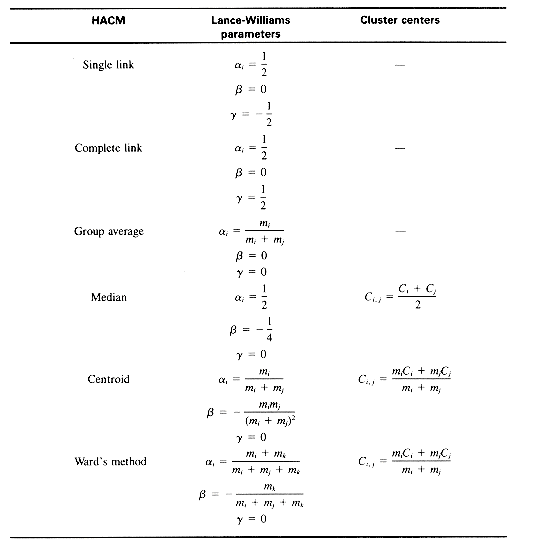
Notes: mi is the number of items in Ci; the dissimilarity measure used for Ward's method must be the increase in variance (section 16.5.5).
 N matrix containing all pairwise dissimilarity values is stored, and the Lance-Williams update formula makes it possible to recalculate the dissimilarity between cluster centers using only the stored values. The time requirement is O (N2), rising to O (N3) if a simple serial scan of the similarity matrix is used; the storage requirement is O (N2). A stored data approach has only an O (N) storage requirement but the need to recalculate the pairwise dissimilarity values for each fusion leads to an O (N3) time requirement. In the sorted matrix approach, the dissimilarity matrix is calculated (O (N2)) and then sorted (O (N2 log N2)) prior to the construction of the hierarchy (O (N2)). The data set need not be stored and the similarity matrix is processed serially, which minimizes disk accesses. However, this approach is suitable only for the single link and complete link methods, which do not require the recalculation of similarities during clustering.
N matrix containing all pairwise dissimilarity values is stored, and the Lance-Williams update formula makes it possible to recalculate the dissimilarity between cluster centers using only the stored values. The time requirement is O (N2), rising to O (N3) if a simple serial scan of the similarity matrix is used; the storage requirement is O (N2). A stored data approach has only an O (N) storage requirement but the need to recalculate the pairwise dissimilarity values for each fusion leads to an O (N3) time requirement. In the sorted matrix approach, the dissimilarity matrix is calculated (O (N2)) and then sorted (O (N2 log N2)) prior to the construction of the hierarchy (O (N2)). The data set need not be stored and the similarity matrix is processed serially, which minimizes disk accesses. However, this approach is suitable only for the single link and complete link methods, which do not require the recalculation of similarities during clustering.16.5.2 Single Link Method
Van Rijsbergen algorithm
SLINK algorithm
 and
and  for a data set numbered 1..N, with the following conditions:
for a data set numbered 1..N, with the following conditions:
 (N) = N
(N) = N
 (i) > i
(i) > i
 (N) =
(N) = 

 (
( (i)) >
(i)) >  (i) for i < N
(i) for i < N (i) is the lowest level (distance or dissimilarity) at which i is no longer the last (i.e., the highest numbered) object in its cluster, and
(i) is the lowest level (distance or dissimilarity) at which i is no longer the last (i.e., the highest numbered) object in its cluster, and  (i) is the last object in the cluster it joins at this level; a mathematical definition for these parameters is provided by Sibson (1973).
(i) is the last object in the cluster it joins at this level; a mathematical definition for these parameters is provided by Sibson (1973)./* initialize pi and lambda for a single point representation */
pi [0] = 0;
lambda[0] = MAXINT;
/*iteratively add the remaining N-1 points to the hierarchy */
for (i = 1; i < N; i++)
{pi [i] = i;
lambda[i] = MAXINT;
/* calculate and store a row of the distance matrix for i */
for (j = 0; j < i-1; j++) distance[j] =calc_distance(i,j);
for (j = 0; j < i-1; j++)
{next = pi[j];
if (lambda[j] < distance[j])
distance[next] = min(distance[next],distance[j]);
else
{distance[next] = min(lambda[j],distance[next]);
pi[j] = i;
lambda[j] = distance[j];
}
}
/* relabel clusters if necessary */
for (j = 0; j <i-1; j++)
{next = pi [j];
if (lambda[next] < lambda [j])
pi[j] = i;
}
}
Minimal spanning tree algorithms
/* initialize lists */
for (i = 0; i < n; i++)
{ndistance[i] = MAXINT;
notintree[i] = i;
}
/* arbitrarily place the Nth point in the MST */
lastpoint = n;
nt = n-1;
/* grow the tree an object at a time */
for ( i = 0; i < n-1;i++)
{/*consider the lastpoint in the tree for the NN list */
for (j = 0; j < nt; j++)
{D = calculate_distance(lastpoint, notintree[j]);
if (D < ndistance[j]
{npoint[j] =lastpoint;
ndistance[j] = D;
}
}
/* find the unconnected point closest to a point in the */
/* tree */
nj = index_of_min(ndistance);
/* add this point to the MST; store this point and their */
/* clustering level */
lastpoint = notintree[nj];
store_in_MST ( lastpoint, npoint[nj], ndistance[nj]);
/* remove lastpoint from notintree list; */
/* close up npoint and ndistance lists */
notintree[nj] = nt;
npoint[nj] = npoint[nt];
ndistance[nj] =ndistance[nt];
nt = nt - 1;
}
}
16.5.3 Complete Link Method
Defays' CLINK algorithm
Voorhees algorithm
 mith similarity of documents in the respective clusters is reached. This requires a sorted list of document-document similarities, and a means of counting the number of similarities seen between any two active clusters. The large number of zero-valued similarities in a typical document collection make it more efficient than its worst case O (N3) time, O (N2) storage requirement would suggest; however it is still very demanding of resources, and El-Hamdouchi and Willett found it impractical to apply it to the largest of the collections they studied.
mith similarity of documents in the respective clusters is reached. This requires a sorted list of document-document similarities, and a means of counting the number of similarities seen between any two active clusters. The large number of zero-valued similarities in a typical document collection make it more efficient than its worst case O (N3) time, O (N2) storage requirement would suggest; however it is still very demanding of resources, and El-Hamdouchi and Willett found it impractical to apply it to the largest of the collections they studied.16.5.4 Group Average Link Method
Voorhees algorithm
16.5.5 Ward's Method
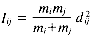
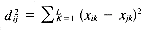
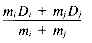
Reciprocal nearest neighbor algorithm
NN(i) = j; NN(j) = k; ...; NN(p) = q; NN(q) = p
16.6 EVALUATION AND VALIDATION
16.6.1 Evaluation
16.6.2 Validation
16.7 UPDATING THE CLUSTER STRUCTURE
16.8 DOCUMENT RETRIEVAL FROM A CLUSTERED DATA SET
16.8.1 Approaches to Retrieval
16.8.2 Cluster Representatives
16.9 CONCLUSION
REFERENCES


