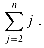
Evaluating this summation yielded a bound of  (n2) on the worst-case running time of the algorithm. This example indicates the general importance of understanding how to manipulate and bound summations. (As we shall see in Chapter 4, summations also arise when we use certain methods to solve recurrences.)
(n2) on the worst-case running time of the algorithm. This example indicates the general importance of understanding how to manipulate and bound summations. (As we shall see in Chapter 4, summations also arise when we use certain methods to solve recurrences.)
Section 3.1 lists several basic formulas involving summations. Section 3.2 offers useful techniques for bounding summations. The formulas in Section 3.1 are given without proof, though proofs for some of them are presented in Section 3.2 to illustrate the methods of that section. Most of the other proofs can be found in any calculus text.
3.1 Summation formulas and properties
Given a sequence a1, a2, . . . of numbers, the finite sum a1 + a2 + . . . +an can be written
If n = 0, the value of the summation is defined to be 0. If n is not an integer, we assume that the upper limit is
Given a sequence a1, a2, . . . of numbers, the infinite sum a1 + a2 +
which is interpreted to mean
If the limit does not exist, the series diverges; otherwise, it converges. The terms of a convergent series cannot always be added in any order. We can, however, rearrange the terms of an absolutely convergent series, that is, a series
For any real number c and any finite sequences a1, a2, . . . , an and b1, b2, . . . , bn,
The linearity property is also obeyed by infinite convergent series.
The linearity property can be exploited to manipulate summations incorporating asymptotic notation. For example,
In this equation, the
The summation
which came up when we analyzed insertion sort, is an arithmetic series and has the value
For real x
is a geometric or exponential series and has the value
When the summation is infinite and |x| < 1, we have the infinite decreasing geometric series
For positive integers n, the nth harmonic number is
Additional formulas can be obtained by integrating or differentiating the formulas above. For example, by differentiating both sides of the infinite geometric series (3.4) and multiplying by x, we get
For any sequence a0, a1, . . . , an,
since each of the terms a1, a2, . . . , an-1 is added in exactly once and subtracted out exactly once. We say that the sum telescopes. Similarly,
As an example of a telescoping sum, consider the series
Since we can rewrite each term as
we get
The finite product a1 a2
If n = 0, the value of the product is defined to be 1. We can convert a formula with a product to a formula with a summation by using the identity
3.1-1
Find a simple formula for
3.1-2
Show that
3.1-3
Show that
3.1-4
Evaluate the sum
3.1-5
Use the linearity property of summations to prove that
3.1-6
Prove that
3.1-7
Evaluate the product
3.1-8
Evaluate the product
There are many techniques available for bounding the summations that describe the running times of algorithms. Here are some of the most frequently used methods.
The most basic way to evaluate a series is to use mathematical induction. As an example, let us prove that the arithmetic series
One need not guess the exact value of a summation in order to use mathematical induction. Induction can be used to show a bound as well. As an example, let us prove that the geometric series
as long as (1/3 + 1/c)
We have to be careful when we use asymptotic notation to prove bounds by induction. Consider the following fallacious proof that
The bug in the argument is that the "constant" hidden by the "big-oh" grows with n and thus is not constant. We have not shown that the same constant works for all n.
Sometimes, a good upper bound on a series can be obtained by bounding each term of the series, and it often suffices to use the largest term to bound the others. For example, a quick upper bound on the arithmetic series (3.1) is
In general, for a series
The technique of bounding each term in a series by the largest term is a weak method when the series can in fact be bounded by a geometric series. Given the series
We can apply this method to bound the summation
for all k
A common bug in applying this method is to show that the ratio of consecutive terms is less than 1 and then to assume that the summation is bounded by a geometric series. An example is the infinite harmonic series, which diverges since
The ratio of the (k + 1)st and kth terms in this series is k/(k + 1) < 1, but the series is not bounded by a decreasing geometric series. To bound a series by a geometric series, one must show that the ratio is bounded away from 1; that is, there must be an r < 1, which is a constant, such that the ratio of all pairs of consecutive terms never exceeds r. In the harmonic series, no such r exists because the ratio becomes arbitrarily close to 1.
One way to obtain bounds on a difficult summation is to express the series as the sum of two or more series by partitioning the range of the index and then to bound each of the resulting series. For example, suppose we try to find a lower bound on the arithmetic series
We can obtain a better lower bound by first splitting the summation. Assume for convenience that n is even. We have
which is an asymptotically tight bound, since
For a summation arising from the analysis of an algorithm, we can often split the summation and ignore a constant number of the initial terms. Generally, this technique applies when each term ak in a summation
since the initial terms of the summation are all constant and there is a constant number of them. We can then use other methods to bound
we observe that the ratio of consecutive terms is
if k
since the second summation is a decreasing geometric series.
The technique of splitting summations can be used to determine asymptotic bounds in much more difficult situations. For example, we can obtain a bound of 0(lg n) on the harmonic series (3.5):
The idea is to split the range 1 to n into
When a summation can be expressed as
The justification for this approximation is shown in Figure 3.1. The summation is represented as the area of the rectangles in the figure, and the integral is the shaded region under the curve. When â(k) is a monotonically decreasing function, we can use a similar method to provide the bounds
The integral approximation (3.10) gives a tight estimate for the nth harmonic number. For a lower bound, we obtain
For the upper bound, we derive the inequality
which yields the bound
3.2-1
Show that
3.2-2
Find an asymptotic upper bound on the summation
3.2-3
Show that the nth harmonic number is
3.2-4
Approximate
3.2-5
Why didn't we use the integral approximation (3.10) directly on
3-1 Bounding summations
Give asymptotically tight bounds on the following summations. Assume that r
Knuth [121] is an excellent reference for the material presented in this chapter. Basic properties of series can be found in any good calculus book, such as Apostol [12] or Thomas and Finney [192].
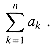
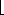 n
n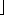 . Similarly, if the sum begins with k = x, where x is not an integer, we assume that the initial value for the summation is
. Similarly, if the sum begins with k = x, where x is not an integer, we assume that the initial value for the summation is 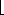 x
x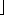 . (Generally, we shall put in floors and ceilings explicitly.) The value of a finite series is always well defined, and its terms can be added in any order.
. (Generally, we shall put in floors and ceilings explicitly.) The value of a finite series is always well defined, and its terms can be added in any order.

 can be written
can be written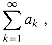
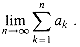
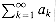 for which the series
for which the series 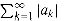 also converges.
also converges.Linearity
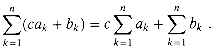
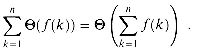
 -notation on the left-hand side applies to the variable k, but on the right-hand side, it applies to n. Such manipulations can also be applied to infinite convergent series.
-notation on the left-hand side applies to the variable k, but on the right-hand side, it applies to n. Such manipulations can also be applied to infinite convergent series.Arithmetic series
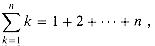

(3.1)
(3.2)
Geometric series
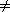 1, the summation
1, the summation

(3.3)

(3.4)
Harmonic series
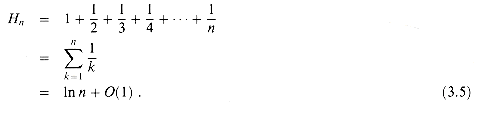
(3.5)
Integrating and differentiating series

(3.6)
Telescoping series

(3.7)
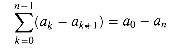
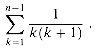
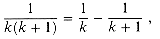
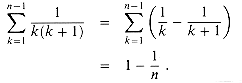
Products


 an can be written
an can be written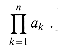

Exercises
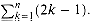
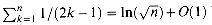 by manipulating the harmonic series.
by manipulating the harmonic series.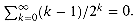
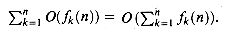
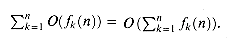

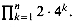
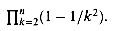
3.2 Bounding summations
Mathematical induction
 evaluates to 1/2n(n + 1). We can easily verify this for n = 1, so we make the inductive assumption that it holds for n and prove that it holds for n + 1. We have
evaluates to 1/2n(n + 1). We can easily verify this for n = 1, so we make the inductive assumption that it holds for n and prove that it holds for n + 1. We have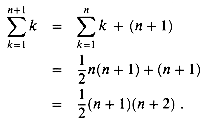
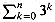 is 0(3n). More specifically, let us prove that
is 0(3n). More specifically, let us prove that 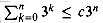 for some constant c. For the initial condition n = 0, we have
for some constant c. For the initial condition n = 0, we have 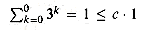 as long as c
as long as c  1. Assuming that the bound holds for n, let us prove that it holds for n + 1. We have
1. Assuming that the bound holds for n, let us prove that it holds for n + 1. We have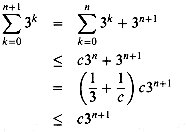
 1 or, equivalently, c
1 or, equivalently, c  3/2. Thus,
3/2. Thus, 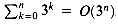 , as we wished to show.
, as we wished to show.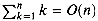 . Certainly,
. Certainly, 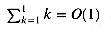 . Assuming the bound for n, we now prove it for n+1:
. Assuming the bound for n, we now prove it for n+1: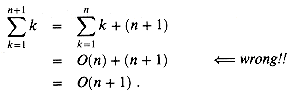
Bounding the terms
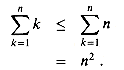
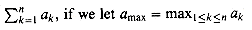 , then
, then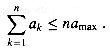
 suppose that ak+1/ak
suppose that ak+1/ak  r for all k
r for all k  0, where r < 1 is a constant. The sum can be bounded by an infinite decreasing geometric series, since ak
0, where r < 1 is a constant. The sum can be bounded by an infinite decreasing geometric series, since ak  a0rk, and thus
a0rk, and thus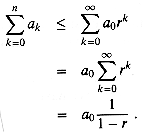
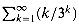 . The first term is 1/3, and the ratio of consecutive terms is
. The first term is 1/3, and the ratio of consecutive terms is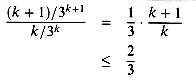
 1. Thus, each term is bounded above by (1/3)(2/3)k, so that
1. Thus, each term is bounded above by (1/3)(2/3)k, so that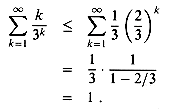
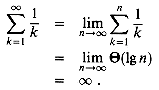
Splitting summations
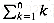 , which has already been shown to have an upper bound of n2. We might attempt to bound each term in the summation by the smallest term, but since that term is 1, we get a lower bound of n for the summation--far off from our upper bound of n2.
, which has already been shown to have an upper bound of n2. We might attempt to bound each term in the summation by the smallest term, but since that term is 1, we get a lower bound of n for the summation--far off from our upper bound of n2.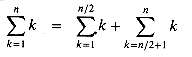
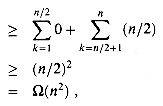
 .
.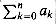 is independent of n. Then for any constant k0 > 0, we can write
is independent of n. Then for any constant k0 > 0, we can write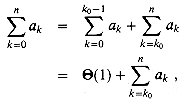
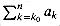 . For example, to find an asymptotic upper bound on
. For example, to find an asymptotic upper bound on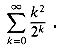

 3. Thus, the summation can be split into
3. Thus, the summation can be split into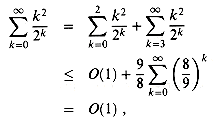
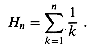
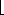 1g n
1g n pieces and upper bound the contribution of each piece by 1. Thus,
pieces and upper bound the contribution of each piece by 1. Thus,
(3.8)
Approximation by integrals
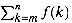 , where â(k) is a monotonically increasing function, we can approximate it by integrals:
, where â(k) is a monotonically increasing function, we can approximate it by integrals: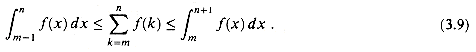
(3.9)
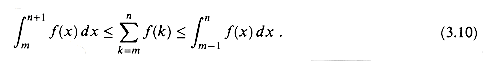
(3.10)

(3.11)
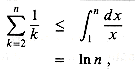

(3.12)
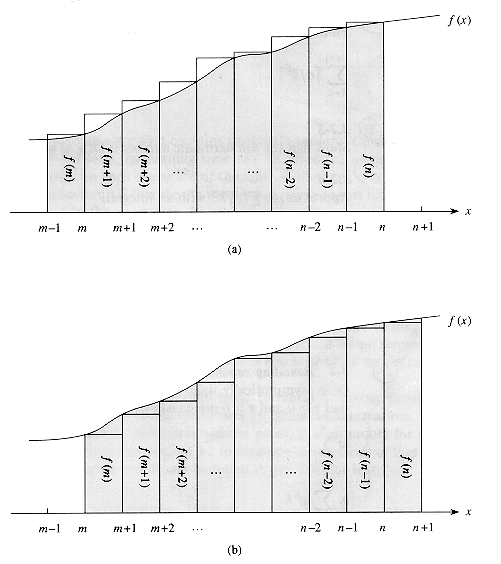
Figure 3.1 Approximation of
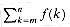 by integrals. The area of each rectangle is shown within the rectangle, and the total rectangle area represents the value of the summation. The integral is represented by the shaded area under the curve. By comparing areas in (a), we get
by integrals. The area of each rectangle is shown within the rectangle, and the total rectangle area represents the value of the summation. The integral is represented by the shaded area under the curve. By comparing areas in (a), we get 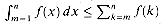 , and then by shifting the rectangles one unit to the right, we get
, and then by shifting the rectangles one unit to the right, we get 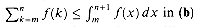 .in (b).
.in (b).Exercises
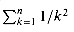 is bounded above by a constant.
is bounded above by a constant.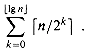
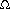 (1g n) by splitting the summation.
(1g n) by splitting the summation.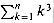 with an integral.
with an integral. to obtain an upper bound on the nth harmonic number?
to obtain an upper bound on the nth harmonic number?Problems
 0 and s
0 and s  0 are constants.
0 are constants.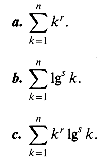
Chapter notes


