 S (read "x is a member of S" or, more briefly, "x is in S"). If x is not a member of S, we write x
S (read "x is a member of S" or, more briefly, "x is in S"). If x is not a member of S, we write x  S. We can describe a set by explicitly listing its members as a list inside braces. For example, we can define a set S to contain precisely the numbers 1, 2, and 3 by writing S = {1, 2, 3}. Since 2 is a member of the set S, we can write 2
S. We can describe a set by explicitly listing its members as a list inside braces. For example, we can define a set S to contain precisely the numbers 1, 2, and 3 by writing S = {1, 2, 3}. Since 2 is a member of the set S, we can write 2  S, and since 4 is not a member, we have 4
S, and since 4 is not a member, we have 4  S. A set cannot contain the same object more than once, and its elements are not ordered. Two sets A and B are equal, written A = B, if they contain the same elements. For example, {1, 2, 3, 1} = {1, 2, 3} = {3, 2, 1}.
S. A set cannot contain the same object more than once, and its elements are not ordered. Two sets A and B are equal, written A = B, if they contain the same elements. For example, {1, 2, 3, 1} = {1, 2, 3} = {3, 2, 1}.We adopt special notations for frequently encountered sets.
1Some authors start the natural numbers with 1 instead of 0. The modern trend seems to be to start with 0.
If all the elements of a set A are contained in a set B, that is, if x
We sometimes define sets in terms of other sets. Given a set A, we can define a set B
Given two sets A and B, we can also define new sets by applying set operations:
Set operations obey the following laws.
Empty set laws:
Idempotency laws:
Commutative laws:
Associative laws:
Distributive laws:
Absorption laws:
DeMorgan's laws:
The first of DeMorgan's laws is illustrated in Figure 5.1, using a Venn diagram, a graphical picture in which sets are represented as regions of the plane.
Often, all the sets under consideration are subsets of some larger set U called the universe. For example, if we are considering various sets made up only of integers, the set Z of integers is an appropriate universe. Given a universe U, we define the complement of a set A as
DeMorgan's laws (5.2) can be rewritten with complements. For any two sets A, B
Two sets A and B are disjoint if they have no elements in common, that is, if
In other words, S forms a partition of S if each element of S appears in exactly one Si
The number of elements in a set is called the cardinality (or size) of the set, denoted |S|. Two sets have the same cardinality if their elements can be put into a one-to-one correspondence. The cardinality of the empty set is
For any two finite sets A and B, we have the identity
from which we can conclude that
If A and B are disjoint, then |A
A finite set of n elements is sometimes called an n-set. A 1-set is called a singleton. A subset of k elements of a set is sometimes called a k-subset.
The set of all subsets of a set S, including the empty set and the set S itself, is denoted 2S and is called the power set of S. For example,
We sometimes care about setlike structures in which the elements are ordered. An ordered pair of two elements a and b is denoted (a, b) and can be defined formally as the set (a, b) = {a, {a, b}}. Thus, the ordered pair (a, b) is not the same as the ordered pair (b, a).
The Cartesian product of two sets A and B, denoted A
For example, {a, b}
The Cartesian product of n sets Al, A2,. . . , An is the set of n-tuples
whose cardinality is
if all sets are finite. We denote an n-fold Cartesian product over a single set A by the set
whose cardinality is |An| = |A|n if A is finite. An n-tuple can also be viewed as a finite sequence of length n (see page 84).
5.1-1
Draw Venn diagrams that illustrate the first of the distributive laws (5.1).
5.1-2
Prove the generalization of DeMorgan's laws to any finite collection of sets:
5.1-3
Prove the generalization of equation (5.3), which is called the principle of inclusion and exclusion:
5.1-4
Show that the set of odd natural numbers is countable.
5.1-5
Show that for any finite set S, the power set 2S has 2|S| elements (that is, there are 2|S| distinct subsets of S).
5.1-6
Give an inductive definition for an n-tuple by extending the set-theoretic definition for an ordered pair.
A binary relation R on two sets A and B is a subset of the Cartesian product A
A binary relation R
for all a
for all a, b
for all a,b,c
A relation that is reflexive, symmetric, and transitive is an equivalence relation. For example, "=" is an equivalence relation on the natural numbers, but "<" is not. If R is an equivalence relation on a set A, then for a
Theorem 5.1
The equivalence classes of any equivalence relation R on a set A form a partition of A, and any partition of A determines an equivalence relation on A for which the sets in the partition are the equivalence classes.
Proof For the first part of the proof, we must show that the equivalence classes of R are nonempty, pairwise-disjoint sets whose union is A. Because R is reflexive, a
For the second part of the proof, let A = {Ai} be a partition of A, and define R = {(a,b): there exists i such that a
A binary relation R on a set A is antisymmetric if
For example, the "
In a partially ordered set A, there may be no single "maximum" element x such that y R x for all y
A partial order R on a set A is a total or linear order if for all a, b
5.2-1
Prove that the subset relation "
5.2-2
Show that for any positive integer n, the relation "equivalent modulo n" is an equivalence relation on the integers. (We say that a
5.2-3
Give examples of relations that are
a. reflexive and symmetric but not transitive,
b. reflexive and transitive but not symmetric,
c. symmetric and transitive but not reflexive.
5.2-4
Let S be a finite set, and let R be an equivalence relation on S
5.2-5
Professor Narcissus claims that if a relation R is symmetric and transitive, then it is also reflexive. He offers the following proof. By symmetry, a R b implies b R a. Transitivity, therefore, implies a R a. Is the professor correct?
Given two sets A and B, a function f is a binary relation on A
Intuitively, the function f assigns an element of B to each element of A. No element of A is assigned two different elements of B, but the same element of B can be assigned to two different elements of A. For example, the binary relation
is a function f : N
is not a function, since (1, 3) and (1, 5) are both in g, and thus for the choice a = 1, there is not precisely one b such that (a, b)
Given a function f : A
A finite sequence of length n is a function f whose domain is the set {0, 1, . . . , n - 1}. We often denote a finite sequence by listing its values:
When the domain of a function f is a Cartesian product, we often omit the extra parentheses surrounding the argument of f. For example, if f : A1
If f : A
The range of f is the image of its domain, that is, f (A). For example, the range of the function f : N
A function is a surjection if its range is its codomain. For example, the function f(n) =
A function f : A
A function f : A
The function is injective, since no element of Z is the image of more than one element of N. It is surjective, since every element of Z appears as the image of some element of N. Hence, the function is bijective. A bijection is sometimes called a one-to-one correspondence, since it pairs elements in the domain and codomain. A bijection from a set A to itself is sometimes called a permutation.
When a function â is bijective, its inverse â-1 is defined as
For example, the inverse of the function â(n) = (-1)n
5.3-1
Let A and B be finite sets, and let f : A
a. if f is injective, then |A|
b. f f is surjective, then |A|
5.3-2
Is the function f (x) = x + 1 bijective when the domain and the codomain are N? Is it bijective when the domain and the codomain are Z?
5.3-3
Give a natural definition for the inverse of a binary relation such that if a relation is in fact a bijective function, its relational inverse is its functional inverse.
5.3-4
Give a bijection from Z to Z
This section presents two kinds of graphs: directed and undirected. The reader should be aware that certain definitions in the literature differ from those given here, but for the most part, the differences are slight. Section 23.1 shows how graphs can be represented in computer memory.
A directed graph (or digraph) G is a pair (V, E), where V is a finite set and E is a binary relation on V. The set V is called the vertex set of G, and its elements are called vertices (singular: vertex). The set E is called the edge set of G, and its elements are called edges. Figure 5.2(a) is a pictorial representation of a directed graph on the vertex set {1, 2, 3, 4, 5, 6}. Vertices are represented by circles in the figure, and edges are represented by arrows. Note that self-loops--edges from a vertex to itself--are possible.
In an undirected graph G = (V, E), the edge set E consists of unordered pairs of vertices, rather than ordered pairs. That is, an edge is a set {u, v}, where u,v
Many definitions for directed and undirected graphs are the same, although certain terms have slightly different meanings in the two contexts. If (u, v) is an edge in a directed graph G = (V, E), we say that (u, v) is incident from or leaves vertex u and is incident to or enters vertex v. For example, the edges leaving vertex 2 in Figure 5.2(a) are (2, 2), (2, 4), and (2, 5). The edges entering vertex 2 are (1, 2) and (2, 2). If (u, v) is an edge in an undirected graph G = (V, E), we say that (u, v) is incident on vertices u and v. In Figure 5.2(b), the edges incident on vertex 2 are (1, 2) and (2, 5).
If (u, v) is an edge in a graph G = (V, E), we say that vertex v is adjacent to vertex u. When the graph is undirected, the adjacency relation is symmetric. When the graph is directed, the adjacency relation is not necessarily symmetric. If v is adjacent to u in a directed graph, we sometimes write u
The degree of a vertex in an undirected graph is the number of edges incident on it. For example, vertex 2 in Figure 5.2(b) has degree 2. In a directed graph, the out-degree of a vertex is the number of edges leaving it, and the in-degree of a vertex is the number of edges entering it. The degree of a vertex in a directed graph is its in-degree plus its out-degree. Vertex 2 in Figure 5.2(a) has in-degree 2, out-degree 3, and degree 5.
A path of length k from a vertex u to a vertex u' in a graph G = (V, E) is a sequence
A subpath of path p =
In a directed graph, a path
An undirected graph is connected if every pair of vertices is connected by a path. The connected components of a graph are the equivalence classes of vertices under the "is reachable from" relation. The graph in Figure 5.2(b) has three connected components: {1, 2, 5}, {3, 6}, and {4}. Every vertex in {1,2,5} is reachable from every other vertex in {1, 2, 5}. An undirected graph is connected if it has exactly one connected component, that is, if every vertex is reachable from every other vertex.
A directed graph is strongly connected if every two vertices are reachable from each other. The strongly connected components of a graph are the equivalence classes of vertices under the "are mutually reachable" relation. A directed graph is strongly connected if it has only one strongly connected component. The graph in Figure 5.2(a) has three strongly connected components: {1, 2, 4, 5}, {3}, and {6}. All pairs of vertices in {1, 2, 4, 5} are mutually reachable. The vertices {3, 6} do not form a strongly connected component, since vertex 6 cannot be reached from vertex 3.
Two graphs G = (V, E) and G' = (V', E') are isomorphic if there exists a bijection f : V
We say that a graph G' = (V', E') is a subgraph of G = (V,E) if V'
The subgraph induced by the vertex set {1, 2, 3, 6} in Figure 5.2(a) appears in Figure 5.2(c) and has the edge set {(1, 2), (2, 2), (6, 3)}.
Given an undirected graph G = (V, E), the directed version of G is the directed graph G' = (V, E'), where (u, v)
Several kinds of graphs are given special names. A complete graph is an undirected graph in which every pair of vertices is adjacent. A bipartite graph is an undirected graph G = (V, E) in which V can be partitioned into two sets V1 and V2 such that (u, v)
There are two variants of graphs that you may occasionally encounter. A multigraph is like an undirected graph, but it can have both multiple edges between vertices and self-loops. A hypergraph is like an undirected graph, but each hyperedge, rather than connecting two vertices, connects an arbitrary subset of vertices. Many algorithms written for ordinary directed and undirected graphs can be adapted to run on these graphlike structures.
5.4-1
Attendees of a faculty party shake hands to greet each other, and each professor remembers how many times he or she shook hands. At the end of the party, the department head sums up the number of times that each professor shook hands. Show that the result is even by proving the handshaking lemma: if G = (V, E) is an undirected graph, then
5.4-2
Show that in an undirected graph, the length of a cycle must be at least 3.
5.4-3
Show that if a directed or undirected graph contains a path between two vertices u and v, then it contains a simple path between u and v. Show that if a directed graph contains a cycle, then it contains a simple cycle.
5.4-4
Show that any connected, undirected graph G = (V, E) satisfies |E|
5.4-5
Verify that in an undirected graph, the "is reachable from" relation is an equivalence relation on the vertices of the graph. Which of the three properties of an equivalence relation hold in general for the "is reachable from" relation on the vertices of a directed graph?
5.4-6
What is the undirected version of the directed graph in Figure 5.2(a)? What is the directed version of the undirected graph in Figure 5.2(b)?
5.4-7
Show that a hypergraph can be represented by a bipartite graph if we let incidence in the hypergraph correspond to adjacency in the bipartite graph. (Hint: Let one set of vertices in the bipartite graph correspond to vertices of the hypergraph, and let the other set of vertices of the bipartite graph correspond to hyperedges.)
As with graphs, there are many related, but slightly different, notions of trees. This section presents definitions and mathematical properties of several kinds of trees. Sections 11.4 and 23.1 describe how trees can be represented in a computer memory.
As defined in Section 5.4, a free tree is a connected, acyclic, undirected graph. We often omit the adjective "free" when we say that a graph is a tree. If an undirected graph is acyclic but possibly disconnected, it is a forest. Many algorithms that work for trees also work for forests. Figure 5.4(a) shows a free tree, and Figure 5.4(b) shows a forest. The forest in Figure 5.4(b) is not a tree because it is not connected. The graph in Figure 5.4(c) is neither a tree nor a forest, because it contains a cycle.
The following theorem captures many important facts about free trees.
Theorem 5.2
Let G = (V, E) be an undirected graph. The following statements are equivalent.
1. G is a free tree.
2. Any two vertices in G are connected by a unique simple path.
3. G is connected, but if any edge is removed from E, the resulting graph is disconnected.
4. G is connected, and |E| = |V| - 1.
5. G is acyclic, and |E| = |V| - 1.
6. G is acyclic, but if any edge is added to E, the resulting graph contains a cycle.
Proof (1)
(2)
(3)
(4)
(5)
(6)
A rooted tree is a free tree in which one of the vertices is distinguished from the others. The distinguished vertex is called the root of the tree. We often refer to a vertex of a rooted tree as a node2 of the tree. Figure 5.6(a) shows a rooted tree on a set of 12 nodes with root 7.
2The term "node" is often used in the graph theory literature as a synonym for "vertex." We shall reserve the term "node" to mean a vertex of a rooted tree.
Consider a node x in a rooted tree T with root r. Any node y on the unique path from r to x is called an ancestor of x. If y is an ancestor of x, then x is a descendant of y. (Every node is both an ancestor and a descendant of itself.) If y is an ancestor of x and x
If the last edge on the path from the root r of a tree T to a node x is (y, x), then y is the parent of x, and x is a child of y. The root is the only node in T with no parent. If two nodes have the same parent, they are siblings. A node with no children is an external node or leaf. A nonleaf node is an internal node.
The number of children of a node x in a rooted tree T is called the degree of x.3 The length of the path from the root r to a node x is the depth of x in T. The largest depth of any node in T is the height of T.
3Notice that the degree of a node depends on whether T is considered to be a rooted tree or a free tree. The degree of a vertex in a free tree is, as in any undirected graph, the number of adjacent vertices. In a rooted tree, however, the degree is the number of children--the parent of a node does not count toward its degree.
An ordered tree is a rooted tree in which the children of each node are ordered. That is, if a node has k children, then there is a first child, a second child, . . . , and a kth child. The two trees in Figure 5.6 are different when considered to be ordered trees, but the same when considered to be just rooted trees.
Binary trees are best described recursively. A binary tree T is a structure defined on a finite set of nodes that either
The binary tree that contains no nodes is called the empty tree or null tree, sometimes denoted NIL. If the left subtree is nonempty, its root is called the left child of the root of the entire tree. Likewise, the root of a nonnull right subtree is the right child of the root of the entire tree. If a subtree is the null tree NIL, we say that the child is absent or missing. Figure 5.7(a) shows a binary tree.
A binary tree is not simply an ordered tree in which each node has degree at most 2. For example, in a binary tree, if a node has just one child, the position of the child--whether it is the left child or the right child--matters. In an ordered tree, there is no distinguishing a sole child as being either left or right. Figure 5.7(b) shows a binary tree that differs from the tree in Figure 5.7(a) because of the position of one node. Considered as ordered trees, however, the two trees are identical.
The positioning information in a binary tree can be represented by the internal nodes of an ordered tree, as shown in Figure 5.7(c). The idea is to replace each missing child in the binary tree with a node having no children. These leaf nodes are drawn as squares in the figure. The tree that results is a full binary tree: each node is either a leaf or has degree exactly 2. There are no degree-1 nodes. Consequently, the order of the children of a node preserves the position information.
The positioning information that distinguishes binary trees from ordered trees can be extended to trees with more than 2 children per node. In a positional tree, the children of a node are labeled with distinct positive integers. The ith child of a node is absent if no child is labeled with integer i. A k-ary tree is a positional tree in which for every node, all children with labels greater than k are missing. Thus, a binary tree is a k-ary tree with k = 2.
A complete k-ary tree is a k-ary tree in which all leaves have the same depth and all internal nodes have degree k. Figure 5.8 shows a complete binary tree of height 3. How many leaves does a complete k-ary tree of height h have? The root has k children at depth 1, each of which has k children at depth 2, etc. Thus, the number of leaves at depth h is kh. Consequently, the height of a complete k-ary tree with n leaves is logk n. The number of internal nodes of a complete k-ary tree of height h is
by equation (3.3). Thus, a complete binary tree has 2h - 1 internal nodes.
5.5-1
Draw all the free trees composed of the 3 vertices A, B, and C. Draw all the rooted trees with nodes A, B, and C with A as the root. Draw all the ordered trees with nodes A, B, and C with A as the root. Draw all the binary trees with nodes A, B, and C with A as the root.
5.5-2
Show that for n
5.5-3
Let G = (V, E) be a directed acyclic graph in which there is a vertex v0
5.5-4
Show by induction that the number of degree-2 nodes in any binary tree is 1 less than the number of leaves.
5.5-5
Show by induction that a binary tree with n nodes has height at least
5.5-6
The internal path length of a full binary tree is the sum, taken over all internal nodes of the tree, of the depth of each node. Likewise, the exernal path length is the sum, taken over all leaves of the tree, of the depth of each leaf. Consider a full binary tree with n internal nodes, internal path length i, and external path length e. Prove that e = i + 2n.
5.5-7
Let us associate a "weight" w(x) = 2-d with each leaf x of depth d in a binary tree T. Prove that
5.5-8
Show that every binary tree with L leaves contains a subtree having between L/3 and 2L/3 leaves, inclusive.
5-1 Graph coloring
A k-coloring of an undirected graph G = (V, E) is a function c: V
a. Show that any tree is 2-colorable.
b. Show that the following are equivalent:
1. G is bipartite.
2. G is 2-colorable.
3. G has no cycles of odd length.
c. Let d be the maximum degree of any vertex in a graph G. Prove that G can be colored with d + 1 colors.
d. Show that if G has O(|V|) edges, then G can be colored with O
5-2 Friendly graphs
Reword each of the following statements as a theorem about undirected graphs, and then prove it. Assume that friendship is symmetric but not reflexive.
a. In any group of n
b. Every group of six people contains either three mutual friends or three mutual strangers.
c. Any group of people can be partitioned into two subgroups such that at least half the friends of each person belong to the subgroup of which that person is not a member.
d. If everyone in a group is the friend of at least half the people in the group, then the group can be seated around a table in such a way that everyone is seated between two friends.
5-3 Bisecting trees
Many divide-and-conquer algorithms that operate on graphs require that the graph be bisected into two nearly equal-sized subgraphs by removing a small number of edges. This problem investigates bisections of trees.
a. Show that by removing a single edge, we can partition the vertices of any n-vertex binary tree into two sets A and B such that |A|
b. Show that the constant 3/4 in part (a) is optimal in the worst case by giving an example of a simple tree whose most evenly balanced partition upon removal of a single edge has |A| = 3n/4.
c. Show that by removing at most O(lg n) edges, we can partition the vertices of any n-vertex tree into two sets A and B such that |A| =
G. Boole pioneered the development of symbolic logic, and he introduced many of the basic set notations in a book published in 1854. Modern set theory was created by G. Cantor during the period 1874-1895. Cantor focused primarily on sets of infinite cardinality. The term "function" is attributed to G. W. Leibnitz, who used it to refer to several kinds of mathematical formulas. His limited definition has been generalized many times. Graph theory originated in 1736, when L. Euler proved that it was impossible to cross each of the seven bridges in the city of Königsberg exactly once and return to the starting point.
A useful compendium of many definitions and results from graph theory is the book by Harary [94].

 denotes the empty set, that is, the set containing no members.
denotes the empty set, that is, the set containing no members. Z denotes the set of integers, that is, the set {. . . , 2, -1, 0, 1, 2, . . .}.
Z denotes the set of integers, that is, the set {. . . , 2, -1, 0, 1, 2, . . .}. R denotes the set of real numbers.
R denotes the set of real numbers. N denotes the set of natural numbers, that is, the set {0, 1, 2, . . .}.1
N denotes the set of natural numbers, that is, the set {0, 1, 2, . . .}.1 A implies x
A implies x  B, then we write A
B, then we write A  B and say that A is a subset of B. A set A is a proper subset of B, written A
B and say that A is a subset of B. A set A is a proper subset of B, written A 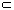 B, if A
B, if A  B but A
B but A  B. (Some authors use the symbol "
B. (Some authors use the symbol "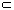 to denote the ordinary subset relation, rather than the proper-subset relation.) For any set A, we have A
to denote the ordinary subset relation, rather than the proper-subset relation.) For any set A, we have A  A. For two sets A and B, we have A = B if and only if A
A. For two sets A and B, we have A = B if and only if A  B and B
B and B  A. For any three sets A, B, and C, if A
A. For any three sets A, B, and C, if A  B and B
B and B  C, then A
C, then A  C. For any set A, we have
C. For any set A, we have 
 A.
A. A by stating a property that distinguishes the elements of B. For example, we can define the set of even integers by {x : x
A by stating a property that distinguishes the elements of B. For example, we can define the set of even integers by {x : x  Z and x/2 is an integer}. The colon in this notation is read "such that." (Some authors use a vertical bar in place of the colon.)
Z and x/2 is an integer}. The colon in this notation is read "such that." (Some authors use a vertical bar in place of the colon.) The intersection of sets A and B is the set
The intersection of sets A and B is the setA
 B = {x : x
B = {x : x  A and x
A and x  B} .
B} . The union of sets A and B is the set
The union of sets A and B is the setA
 B = {x : x
B = {x : x  A and x
A and x  B} .
B} . The difference between two sets A and B is the set
The difference between two sets A and B is the setA - B = {x : x  A and x
A and x  B} .
B} .
A
 A = A,
A = A,A
 A = A.
A = A.A
 B = B
B = B  A,
A,A
 B = B
B = B  A.
A.A
 (B
(B  C) = (A
C) = (A  B)
B)  C,
C,A
 (B
(B  C) = (A
C) = (A  B)
B)  C.
C.A
 (B
(B  C) = (A
C) = (A  B)
B)  (A
(A  C),
C),A
 (B
(B  C) = (A
C) = (A  B)
B)  (A
(A  C).
C).(5.1)
A
 (A
(A  B) = A,
B) = A,A
 (A
(A  B) = A.
B) = A.A - (B
 C) = (A - B)
C) = (A - B)  (A - C),
(A - C),A - (B
 C) = (A - B)
C) = (A - B)  (A - C).
(A - C).(5.2)

Figure 5.1 A Venn diagram illustrating the first of DeMorgan's laws (5.2). Each of the sets A, B, and C is represented as a circle in the plane.
 . For any set A
. For any set A  U, we have the following laws:
U, we have the following laws:
 U, we have
U, we have
 . A collection S = {Si} of nonempty sets forms a partition of a set S if
. A collection S = {Si} of nonempty sets forms a partition of a set S if the sets are pairwise disjoint, that is, Si, Sj
the sets are pairwise disjoint, that is, Si, Sj  S and i
S and i  j imply
j imply  , and
, and their union is S, that is,
their union is S, that is,
 S.
S. . If the cardinality of a set is a natural number, we say the set is finite; otherwise, it is infinite. An infinite set that can be put into a one-to-one correspondence with the natural numbers N is countably infinite; otherwise, it is uncountable. The integers Z are countable, but the reals R are uncountable.
. If the cardinality of a set is a natural number, we say the set is finite; otherwise, it is infinite. An infinite set that can be put into a one-to-one correspondence with the natural numbers N is countably infinite; otherwise, it is uncountable. The integers Z are countable, but the reals R are uncountable.|A
 B| = |A| + |B| - |A
B| = |A| + |B| - |A  B| ,
B| ,(5.3)
|A
 B|
B|  |A| + |B| .
|A| + |B| . B| = 0 and thus |A
B| = 0 and thus |A  B| = |A| + |B|. If A
B| = |A| + |B|. If A  B, then |A|
B, then |A|  |B|.
|B|. . The power set of a finite set S has cardinality 2|S|.
. The power set of a finite set S has cardinality 2|S|. B, is the set of all ordered pairs such that the first element of the pair is an element of A and the second is an element of B. More formally,
B, is the set of all ordered pairs such that the first element of the pair is an element of A and the second is an element of B. More formally,A
 B = {(a,b) : a
B = {(a,b) : a  A and b
A and b  B}.
B}. {a, b, c} = {(a, a), (a, b), (a, c), (b, a), (b, b), (b, c)}. When A and B are finite sets, the cardinality of their Cartesian product is
{a, b, c} = {(a, a), (a, b), (a, c), (b, a), (b, b), (b, c)}. When A and B are finite sets, the cardinality of their Cartesian product is|A
 B| = |A|
B| = |A|  |B| .
|B| .(5.4)
A1
 A2
A2 



 An = {(a1,a2,...,an):ai
An = {(a1,a2,...,an):ai  Ai,i = 1, 2,...,n} ,
Ai,i = 1, 2,...,n} ,|A1
 A2
A2 



 An| = |A1|
An| = |A1|  |A2|
|A2| 

 |An|
|An|An = A
 A
A 



 A ,
A ,Exercises

|A1
 A2
A2 



 An| =
An| =|A1| + |A2| +


 + |An|
+ |An|-|A1
 A2| - |A1
A2| - |A1  A3| -
A3| - 

 (all pairs)
(all pairs)+|A1
 A2
A2  A3
A3 +
+ 

 (all triples)
(all triples)
+(-1)n-1 |A1
 A2
A2 



 An| .
An| .5.2 Relations
 B. If (a, b)
B. If (a, b)  R, we sometimes write a R b. When we say that R is a binary relation on a set A, we mean that R is a subset of A
R, we sometimes write a R b. When we say that R is a binary relation on a set A, we mean that R is a subset of A  A. For example, the "less than" relation on the natural numbers is the set {(a,b): a,b
A. For example, the "less than" relation on the natural numbers is the set {(a,b): a,b  N and a < b}. An n-ary relation on sets A1, A2, . . . , An is a subset of A1
N and a < b}. An n-ary relation on sets A1, A2, . . . , An is a subset of A1  A2
A2 



 An.
An. A
A  A is reflexive if
A is reflexive ifa R a
 A. For example, "=" and "
A. For example, "=" and " " are reflexive relations on N, but "<" is not. The relation R is symmetric if
" are reflexive relations on N, but "<" is not. The relation R is symmetric ifa R b implies b R a
 A. For example, "=" is symmetric, but "<" and "
A. For example, "=" is symmetric, but "<" and " " are not. The relation R is transitive if
" are not. The relation R is transitive ifa R b and b R c imply a R c
 A. For example, the relations "<," "
A. For example, the relations "<," " ," and "=" are transitive, but the relation R = {(a, b): a, b
," and "=" are transitive, but the relation R = {(a, b): a, b  N and a = b - 1 } is not, since 3 R 4 and 4 R 5 do not imply 3 R 5.
N and a = b - 1 } is not, since 3 R 4 and 4 R 5 do not imply 3 R 5. A, the equivalence class of a is the set [a] = {b
A, the equivalence class of a is the set [a] = {b  A: a R b}, that is, the set of all elements equivalent to A. For example, if we define R = {(a, b): a, b
A: a R b}, that is, the set of all elements equivalent to A. For example, if we define R = {(a, b): a, b  N and a + b is an even number}, then R is an equivalence relation, since a + a is even (reflexive), a + b is even implies b + a is even (symmetric), and a + b is even and b + c is even imply a + c is even (transitive). The equivalence class of 4 is [4] = {0, 2, 4, 6, . . .}, and the equivalence class of 3 is [3] = {1, 3, 5, 7, . . .}. A basic theorem of equivalence classes is the following.
N and a + b is an even number}, then R is an equivalence relation, since a + a is even (reflexive), a + b is even implies b + a is even (symmetric), and a + b is even and b + c is even imply a + c is even (transitive). The equivalence class of 4 is [4] = {0, 2, 4, 6, . . .}, and the equivalence class of 3 is [3] = {1, 3, 5, 7, . . .}. A basic theorem of equivalence classes is the following. [a], and so the equivalence classes are nonempty; moreover, since every element a
[a], and so the equivalence classes are nonempty; moreover, since every element a  A belongs to the equivalence class [a], the union of the equivalence classes is A. It remains to show that the equivalence classes are pairwise disjoint, that is, if two equivalence classes [a] and [b] have an element c in common, then they are in fact the same set. Now a R c and b R c, which by symmetry and transitivity imply a R b. Thus, for any arbitrary element x
A belongs to the equivalence class [a], the union of the equivalence classes is A. It remains to show that the equivalence classes are pairwise disjoint, that is, if two equivalence classes [a] and [b] have an element c in common, then they are in fact the same set. Now a R c and b R c, which by symmetry and transitivity imply a R b. Thus, for any arbitrary element x  [a], we have x R a implies x R b, and thus [a]
[a], we have x R a implies x R b, and thus [a]  [b]. Similarly, [b]
[b]. Similarly, [b]  [a], and thus [a] = [b].
[a], and thus [a] = [b]. Ai and b
Ai and b  Ai}. We claim that R is an equivalence relation on A. Reflexivity holds, since a
Ai}. We claim that R is an equivalence relation on A. Reflexivity holds, since a  Ai implies a R a. Symmetry holds, because if a R b, then a and b are in the same set Ai, and hence b R a. If a R b and b R c, then all three elements are in the same set, and thus a R c and transitivity holds. To see that the sets in the partition are the equivalence classes of R, observe that if a
Ai implies a R a. Symmetry holds, because if a R b, then a and b are in the same set Ai, and hence b R a. If a R b and b R c, then all three elements are in the same set, and thus a R c and transitivity holds. To see that the sets in the partition are the equivalence classes of R, observe that if a  Ai, then x
Ai, then x  [a] implies x
[a] implies x  Ai, and x
Ai, and x  Ai implies x
Ai implies x  [a].
[a]. a R b and b R a imply a = b .
 " relation on the natural numbers is antisymmetric, since a
" relation on the natural numbers is antisymmetric, since a  b and b
b and b  a imply a = b. A relation that is reflexive, antisymmetric, and transitive is a partial order, and we call a set on which a partial order is defined a partially ordered set. For example, the relation "is a descendant of" is a partial order on the set of all people (if we view individuals as being their own descendants).
a imply a = b. A relation that is reflexive, antisymmetric, and transitive is a partial order, and we call a set on which a partial order is defined a partially ordered set. For example, the relation "is a descendant of" is a partial order on the set of all people (if we view individuals as being their own descendants). A. Instead, there may several maximal elements x such that for no y
A. Instead, there may several maximal elements x such that for no y  A is it the case that x R y. For example, in a collection of different-sized boxes there may be several maximal boxes that don't fit inside of any other box, yet no single "maximum" box into which any other box will fit.
A is it the case that x R y. For example, in a collection of different-sized boxes there may be several maximal boxes that don't fit inside of any other box, yet no single "maximum" box into which any other box will fit. A, we have a R b or b R a, that is, if every pairing of elements of A can be related by R. For example, the relation "
A, we have a R b or b R a, that is, if every pairing of elements of A can be related by R. For example, the relation " " is a total order on the natural numbers, but the "is a descendant of" relation is not a total order on the set of all people, since there are individuals neither of whom is descended from the other.
" is a total order on the natural numbers, but the "is a descendant of" relation is not a total order on the set of all people, since there are individuals neither of whom is descended from the other.Exercises
 on all subsets of Z is a partial order but not a total order.
on all subsets of Z is a partial order but not a total order. b (mod n) if there exists an integer q such that a - b =qn.) Into what equivalence classes does this relation partition the integers?
b (mod n) if there exists an integer q such that a - b =qn.) Into what equivalence classes does this relation partition the integers? S. Show that if in addition R is antisymmetric, then the equivalence classes of S with respect to R are singletons.
S. Show that if in addition R is antisymmetric, then the equivalence classes of S with respect to R are singletons.5.3 Functions
 B such that for all a
B such that for all a  A, there exists precisely one b
A, there exists precisely one b  B such that (a,b)
B such that (a,b) 
 . The set A is called the domain of f, and the set B is called the codomain of f. We sometimes write f: A
. The set A is called the domain of f, and the set B is called the codomain of f. We sometimes write f: A  B; and if (a, b)
B; and if (a, b)  f, we write b = f (a), since b is uniquely determined by the choice of a.
f, we write b = f (a), since b is uniquely determined by the choice of a.f = {(a,b) : a  N and b = a mod 2 }
N and b = a mod 2 } {0,1}, since for each natural number a, there is exactly one value b in {0, 1} such that b = a mod 2. For this example 0 = f (0), 1 = f (1), 0 = f (2), etc. In contrast, the binary relation
{0,1}, since for each natural number a, there is exactly one value b in {0, 1} such that b = a mod 2. For this example 0 = f (0), 1 = f (1), 0 = f (2), etc. In contrast, the binary relationg = {(a,b) : a  N and a + b is even}
N and a + b is even} g.
g. B, if b = f (a), we say that a is the argument of f and that b is the value of f at a. We can define a function by stating its value for every element of its domain. For example, we might define f (n) = 2n for n
B, if b = f (a), we say that a is the argument of f and that b is the value of f at a. We can define a function by stating its value for every element of its domain. For example, we might define f (n) = 2n for n  N, which means f = {(n,2n): n
N, which means f = {(n,2n): n  N}. Two functions f and g are equal if they have the same domain and codomain and if, for all a in the domain, f (a) = g(a).
N}. Two functions f and g are equal if they have the same domain and codomain and if, for all a in the domain, f (a) = g(a). f (0), f (1), . . . , f (n - 1)
f (0), f (1), . . . , f (n - 1) . An infinite sequence is a function whose domain is the set N of natural numbers. For example, the Fibonacci sequence, defined by (2.13), is the infinite sequence
. An infinite sequence is a function whose domain is the set N of natural numbers. For example, the Fibonacci sequence, defined by (2.13), is the infinite sequence  0, 1, 1, 2, 3, 5, 8, 13, 21, . . .
0, 1, 1, 2, 3, 5, 8, 13, 21, . . . .
. A2
A2 



 An
An  B, we would write b = f (a1, a2, . . . , an) instead of b = f ((a1, a2, . . . , an)). We also call each ai, an argument to the function f , though technically the (single) argument to f is the n-tuple (a1, a2, . . . ,an).
B, we would write b = f (a1, a2, . . . , an) instead of b = f ((a1, a2, . . . , an)). We also call each ai, an argument to the function f , though technically the (single) argument to f is the n-tuple (a1, a2, . . . ,an). B is a function and b = f (a), then we sometimes say that b is the image of a under f . The image of a set A'
B is a function and b = f (a), then we sometimes say that b is the image of a under f . The image of a set A' A under f is defined by
A under f is defined byf(A' = {b  B : b = f(a) for some a
B : b = f(a) for some a  A'} .
A'} . N defined by f (n) = 2n is f (N) = {m : m = 2n for some n
N defined by f (n) = 2n is f (N) = {m : m = 2n for some n  N}.
N}. n/2
n/2 is a surjective function from N to N, since every element in N appears as the value of f for some argument. In contrast, the function f(n) = 2n is not a surjective function from N to N, since no argument to f can produce 3 as a value. The function f (n) = 2n is, however, a surjective function from the natural numbers to the even numbers. A surjection f : A
is a surjective function from N to N, since every element in N appears as the value of f for some argument. In contrast, the function f(n) = 2n is not a surjective function from N to N, since no argument to f can produce 3 as a value. The function f (n) = 2n is, however, a surjective function from the natural numbers to the even numbers. A surjection f : A  B is sometimes described as mapping A onto B. When we say that f is onto, we mean that it is surjective.
B is sometimes described as mapping A onto B. When we say that f is onto, we mean that it is surjective. B is an injection if distinct arguments to â produce distinct values, that is, if a
B is an injection if distinct arguments to â produce distinct values, that is, if a  a' implies â(a) = â(a'). For example, the function f (n) = 2n is an injective function from N to N, since each even number b is the image under â of at most one element of the domain, namely b/2. The function f (n) =
a' implies â(a) = â(a'). For example, the function f (n) = 2n is an injective function from N to N, since each even number b is the image under â of at most one element of the domain, namely b/2. The function f (n) =  n/2
n/2 is not injective, since the value 1 is produced by two arguments: 2 and 3. An injection is sometimes called a one-to-one function.
is not injective, since the value 1 is produced by two arguments: 2 and 3. An injection is sometimes called a one-to-one function. B is a bijection if it is injective and surjective. For example, the function f (n) = (-1)n
B is a bijection if it is injective and surjective. For example, the function f (n) = (-1)n  n/2
n/2 is a bijection from N to Z:
is a bijection from N to Z:0

 0 ,
0 ,1
 -1 ,
-1 ,2
 1 ,
1 ,3
 -2 ,
-2 ,4
 2 ,
2 ,
f-1(b) = a if and only if f(a) = b.
 n/2
n/2 is
is
Exercises
 B be a function. Show that
B be a function. Show that |B|;
|B|; |B|.
|B|. Z.
Z.5.4 Graphs
 V and u
V and u  v. By convention, we use the notation (u, v) for an edge, rather than the set notation {u,v}, and (u,v) and (v, u) are considered to be the same edge. In an undirected graph, self-loops are forbidden, and so every edge consists of exactly two distinct vertices. Figure 5.2(b) is a pictorial representation of an undirected graph on the vertex set {1, 2, 3, 4, 5, 6}.
v. By convention, we use the notation (u, v) for an edge, rather than the set notation {u,v}, and (u,v) and (v, u) are considered to be the same edge. In an undirected graph, self-loops are forbidden, and so every edge consists of exactly two distinct vertices. Figure 5.2(b) is a pictorial representation of an undirected graph on the vertex set {1, 2, 3, 4, 5, 6}.
Figure 5.2 Directed and undirected graphs. (a) A directed graph G = (V, E), where V = {1, 2, 3, 4, 5, 6} and E = {(1, 2), (2, 2), (2, 4), (2, 5), (4, 1), (4, 5), (5, 4), (6, 3)}. The edge (2, 2) is a self-loop. (b) An undirected graph G = (V, E), where V = {1, 2, 3, 4, 5, 6} and E = {(1, 2), (1, 5), (2, 5), (3, 6)}. The vertex 4 is isolated. (c) The subgraph of the graph in part (a) induced by the vertex set {1, 2, 3, 6}.
 v. In parts (a) and (b) of Figure 5.2, vertex 2 is adjacent to vertex 1, since the edge (1, 2) belongs to both graphs. Vertex 1 is not adjacent to vertex 2 in Figure 5.2(a), since the edge (2, 1) does not belong to the graph.
v. In parts (a) and (b) of Figure 5.2, vertex 2 is adjacent to vertex 1, since the edge (1, 2) belongs to both graphs. Vertex 1 is not adjacent to vertex 2 in Figure 5.2(a), since the edge (2, 1) does not belong to the graph. v0, v1, v2, . . . , vk
v0, v1, v2, . . . , vk of vertices such that u = v0, u' = vk, and (vi - 1, vi)
of vertices such that u = v0, u' = vk, and (vi - 1, vi)  E for i = 1, 2, . . . , k. The length of the path is the number of edges in the path. The path contains the vertices v0, v1 , . . . , vk and the edges (v0, v1), (v1, v2), . . . , (vk - 1, vk). If there is a path p from u to u', we say that u' is reachable from u via p, which we sometimes write as
E for i = 1, 2, . . . , k. The length of the path is the number of edges in the path. The path contains the vertices v0, v1 , . . . , vk and the edges (v0, v1), (v1, v2), . . . , (vk - 1, vk). If there is a path p from u to u', we say that u' is reachable from u via p, which we sometimes write as  if G is directed. A path is simple if all vertices in the path are distinct. In Figure 5.2(a), the path
if G is directed. A path is simple if all vertices in the path are distinct. In Figure 5.2(a), the path  1, 2, 5, 4
1, 2, 5, 4 is a simple path of length 3. The path
is a simple path of length 3. The path  2, 5, 4, 5
2, 5, 4, 5 is not simple.
is not simple. v0, v1, . . . , vk
v0, v1, . . . , vk is a contiguous subsequence of its vertices. That is, for any 0
is a contiguous subsequence of its vertices. That is, for any 0  i
i  j
j  k, the subsequence of vertices
k, the subsequence of vertices  vi, vi + 1, . . . ,vj
vi, vi + 1, . . . ,vj is a subpath of p.
is a subpath of p. v0, v1, . . . , vk
v0, v1, . . . , vk forms a cycle if v0 = vk and the path contains at least one edge. The cycle is simple if, in addition, v1, v2, . . . , vk are distinct. A self-loop is a cycle of length 1. Two paths
forms a cycle if v0 = vk and the path contains at least one edge. The cycle is simple if, in addition, v1, v2, . . . , vk are distinct. A self-loop is a cycle of length 1. Two paths  v0, v1, v2, . . . , vk - 1, v0
v0, v1, v2, . . . , vk - 1, v0 and
and  v'0, v'1, v'2, . . . , v'k - 1,v'0
v'0, v'1, v'2, . . . , v'k - 1,v'0 form the same cycle if there exists an integer j such that v'i = v(i + j) modk for i = 0, 1, . . . , k - 1. In Figure 5.2(a), the path
form the same cycle if there exists an integer j such that v'i = v(i + j) modk for i = 0, 1, . . . , k - 1. In Figure 5.2(a), the path  1, 2, 4, 1
1, 2, 4, 1 forms the same cycle as the paths
forms the same cycle as the paths  2, 4, 1, 2
2, 4, 1, 2 and
and  4, 1, 2, 4
4, 1, 2, 4 . This cycle is simple, but the cycle
. This cycle is simple, but the cycle  1, 2, 4, 5, 4, 1
1, 2, 4, 5, 4, 1 is not. The cycle
is not. The cycle  2, 2
2, 2 formed by the edge (2, 2) is a self-loop. A directed graph with no self-loops is simple. In an undirected graph, a path
formed by the edge (2, 2) is a self-loop. A directed graph with no self-loops is simple. In an undirected graph, a path  v0, vl, . . . , vk
v0, vl, . . . , vk forms a cycle if v0 = vk and v1, v2, . . . , vk are distinct. For example, in Figure 5.2(b), the path
forms a cycle if v0 = vk and v1, v2, . . . , vk are distinct. For example, in Figure 5.2(b), the path  1, 2, 5, 1
1, 2, 5, 1 is a cycle. A graph with no cycles is acyclic.
is a cycle. A graph with no cycles is acyclic. V' such that (u, v)
V' such that (u, v)  E if and only if (f(u), f(v))
E if and only if (f(u), f(v))  E'. In other words, we can relabel the vertices of G to be vertices of G', maintaining the corresponding edges in G and G'. Figure 5.3(a) shows a pair of isomorphic graphs G and G' with respective vertex sets V = {1, 2, 3, 4, 5, 6} and V' = {u, v, w, x, y, z}. The mapping from V to V' given by f(1) = u, f(2) = v, f(3) = w, f(4) = x, f(5) = y, f(6) = z is the required bijective function. The graphs in Figure 5.3(b) are not isomorphic. Although both graphs have 5 vertices and 7 edges, the top graph has a vertex of degree 4 and the bottom graph does not.
E'. In other words, we can relabel the vertices of G to be vertices of G', maintaining the corresponding edges in G and G'. Figure 5.3(a) shows a pair of isomorphic graphs G and G' with respective vertex sets V = {1, 2, 3, 4, 5, 6} and V' = {u, v, w, x, y, z}. The mapping from V to V' given by f(1) = u, f(2) = v, f(3) = w, f(4) = x, f(5) = y, f(6) = z is the required bijective function. The graphs in Figure 5.3(b) are not isomorphic. Although both graphs have 5 vertices and 7 edges, the top graph has a vertex of degree 4 and the bottom graph does not. V and E'
V and E'  E. Given a set V'
E. Given a set V'  V, the subgraph of G induced by V' is the graph G' = (V', E'), where
V, the subgraph of G induced by V' is the graph G' = (V', E'), whereE' = {(u, v)  E: u, v
E: u, v  V'} .
V'} .
Figure 5.3 (a) A pair of isomorphic graphs. The vertices of the top graph are mapped to the vertices of the bottom graph by f(1) = u, f(2) = v, f(3) = w, f(4) = x, f(5) = y, f(6) = z. (b) Two graphs that are not isomorphic, since the top graph has a vertex of degree 4 and the bottom graph does not.
 E' if and only if (u, v)
E' if and only if (u, v)  E. That is, each undirected edge (u, v) in G is replaced in the directed version by the two directed edges (u, v) and (v, u). Given a directed graph G =(V, E), the undirected version of G is the undirected graph G' = (V, E'), where (u, v)
E. That is, each undirected edge (u, v) in G is replaced in the directed version by the two directed edges (u, v) and (v, u). Given a directed graph G =(V, E), the undirected version of G is the undirected graph G' = (V, E'), where (u, v)  E' if and only if u
E' if and only if u  v and (u, v)
v and (u, v)  E. That is, the undirected version contains the edges of G "with their directions removed" and with self-loops eliminated. (Since (u, v) and (v, u) are the same edge in an undirected graph, the undirected version of a directed graph contains it only once, even if the directed graph contains both edges (u, v) and (v, u). In a directed graph G = (V, E), a neighbor of a vertex u is any vertex that is adjacent to u in the undirected version of G. That is, v is a neighbor of u if either (u, v)
E. That is, the undirected version contains the edges of G "with their directions removed" and with self-loops eliminated. (Since (u, v) and (v, u) are the same edge in an undirected graph, the undirected version of a directed graph contains it only once, even if the directed graph contains both edges (u, v) and (v, u). In a directed graph G = (V, E), a neighbor of a vertex u is any vertex that is adjacent to u in the undirected version of G. That is, v is a neighbor of u if either (u, v)  E or (v, u)
E or (v, u)  E. In an undirected graph, u and v are neighbors if they are adjacent.
E. In an undirected graph, u and v are neighbors if they are adjacent. E implies either u
E implies either u  V1 and v
V1 and v  V2 or u
V2 or u  V2 and v
V2 and v  V1. That is, all edges go between the two sets V1and V2. An acyclic, undirected graph is a forest, and a connected, acyclic, undirected graph is a (free) tree (see Section 5.5). We often take the first letters of "directed acyclic graph" and call such a graph a dag.
V1. That is, all edges go between the two sets V1and V2. An acyclic, undirected graph is a forest, and a connected, acyclic, undirected graph is a (free) tree (see Section 5.5). We often take the first letters of "directed acyclic graph" and call such a graph a dag.Exercises

 |V| - 1.
|V| - 1.5.5 Trees
5.5.1 Free trees
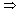 (2): Since a tree is connected, any two vertices in G are connected by at least one simple path. Let u and v be vertices that are connected by two distinct simple paths p1 and p2, as shown in Figure 5.5. Let w be the vertex at which the paths first diverge; that is, w is the first vertex on both p1 and p2 whose successor on p1 is x and whose successor on p2 is y, where x
(2): Since a tree is connected, any two vertices in G are connected by at least one simple path. Let u and v be vertices that are connected by two distinct simple paths p1 and p2, as shown in Figure 5.5. Let w be the vertex at which the paths first diverge; that is, w is the first vertex on both p1 and p2 whose successor on p1 is x and whose successor on p2 is y, where x  y. Let z be the first vertex at which the paths reconverge; that is, z is the first vertex following w on p1 that is also on p2. Let p' be the subpath of p1 from w through x to z, and let p\" be the subpath of p2 from w through y to z. Paths p' and p\" share no vertices except their endpoints. Thus, the path obtained by concatenating p' and the reverse of p\"is a cycle. This is a contradiction. Thus, if G is a tree, there can be at most one path between two vertices.
y. Let z be the first vertex at which the paths reconverge; that is, z is the first vertex following w on p1 that is also on p2. Let p' be the subpath of p1 from w through x to z, and let p\" be the subpath of p2 from w through y to z. Paths p' and p\" share no vertices except their endpoints. Thus, the path obtained by concatenating p' and the reverse of p\"is a cycle. This is a contradiction. Thus, if G is a tree, there can be at most one path between two vertices.
Figure 5.4 (a) A free tree. (b) A forest. (c) A graph that contains a cycle and is therefore neither a tree nor a forest.

Figure 5.5 A step in the proof of Theorem 5.2: if (1) G is a free tree, then (2) any two vertices in G are connected by a unique simple path. Assume for the sake of contradiction that vertices u and v are connected by two distinct simple paths p1 and p2. These paths first diverge at vertex w, and they first reconverge at vertex z. The path p' concatenated with the reverse of the path p\" forms a cycle, which yields the contradiction.
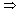 (3): If any two vertices in G are connected by a unique simple path, then G is connected. Let (u, v) be any edge in E. This edge is a path from u to v, and so it must be the unique path from u to v. If we remove (u, v) from G, there is no path from u to v, and hence its removal disconnects G.
(3): If any two vertices in G are connected by a unique simple path, then G is connected. Let (u, v) be any edge in E. This edge is a path from u to v, and so it must be the unique path from u to v. If we remove (u, v) from G, there is no path from u to v, and hence its removal disconnects G. (4): By assumption, the graph G is connected, and by Exercise 5.4-4, we have |E|
(4): By assumption, the graph G is connected, and by Exercise 5.4-4, we have |E|  |V| - 1. We shall prove |E|
|V| - 1. We shall prove |E|  |V| - 1 by induction. A connected graph with n = 1 or n = 2 vertices has n - 1 edges. Suppose that G has n
|V| - 1 by induction. A connected graph with n = 1 or n = 2 vertices has n - 1 edges. Suppose that G has n  3 vertices and that all graphs satisfying (3) with fewer than n vertices also satisfy |E|
3 vertices and that all graphs satisfying (3) with fewer than n vertices also satisfy |E|  |V| - 1. Removing an arbitrary edge from G separates the graph into k
|V| - 1. Removing an arbitrary edge from G separates the graph into k  2 connected components (actually k = 2). Each component satisfies (3), or else G would not satisfy (3). Thus, by induction, the number of edges in all components combined is at most |V| - k
2 connected components (actually k = 2). Each component satisfies (3), or else G would not satisfy (3). Thus, by induction, the number of edges in all components combined is at most |V| - k  |V| - 2. Adding in the removed edge yields |E|
|V| - 2. Adding in the removed edge yields |E|  |V| - 1.
|V| - 1. (5): Suppose that G is connected and that |E| = |V| - 1. We must show that G is acyclic. Suppose that G has a cycle containing k vertices v1, v2, . . . , vk. Let Gk = (Vk, Ek) be the subgraph of G consisting of the cycle. Note that |Vk| = |Ek| = k. If k < |V|, there must be a vertex vk+1
(5): Suppose that G is connected and that |E| = |V| - 1. We must show that G is acyclic. Suppose that G has a cycle containing k vertices v1, v2, . . . , vk. Let Gk = (Vk, Ek) be the subgraph of G consisting of the cycle. Note that |Vk| = |Ek| = k. If k < |V|, there must be a vertex vk+1  V - Vk that is adjacent to some vertex vi
V - Vk that is adjacent to some vertex vi  Vk, since G is connected. Define Gk+1 = (Vk+1, Ek+1) to be the subgraph of G with Vk+1 = Vk
Vk, since G is connected. Define Gk+1 = (Vk+1, Ek+1) to be the subgraph of G with Vk+1 = Vk {vk+1} and Ek+1 = Ek
{vk+1} and Ek+1 = Ek {(v1, vk+1)}. Note that |Vk+1| = |Ek+1| = k+1. If k+1 < n, we can continue, defining Gk+2 in the same manner, and so forth, until we obtain Gn = (Vn, En), where n = |V|, Vn = V, and |En| = |Vn| = |V|. Since Gn is a subgraph of G, we have En
{(v1, vk+1)}. Note that |Vk+1| = |Ek+1| = k+1. If k+1 < n, we can continue, defining Gk+2 in the same manner, and so forth, until we obtain Gn = (Vn, En), where n = |V|, Vn = V, and |En| = |Vn| = |V|. Since Gn is a subgraph of G, we have En  E, and hence |E|
E, and hence |E|  |V|, which contradicts the assumption that |E| = |V| - 1. Thus, G is acyclic.
|V|, which contradicts the assumption that |E| = |V| - 1. Thus, G is acyclic. (6): Suppose that G is acyclic and that |E | = |V | - 1. Let k be the number of connected components of G. Each connected component is a free tree by definition, and since (1) implies (5), the sum of all edges in all connected components of G is |V | - k. Consequently, we must have k = 1, and G is in fact a tree. Since (1) implies (2), any two vertices in G are connected by a unique simple path. Thus, adding any edge to G creates a cycle.
(6): Suppose that G is acyclic and that |E | = |V | - 1. Let k be the number of connected components of G. Each connected component is a free tree by definition, and since (1) implies (5), the sum of all edges in all connected components of G is |V | - k. Consequently, we must have k = 1, and G is in fact a tree. Since (1) implies (2), any two vertices in G are connected by a unique simple path. Thus, adding any edge to G creates a cycle. (1): Suppose that G is acyclic but that if any edge is added to E, a cycle is created. We must show that G is connected. Let u and v be arbitrary vertices in G. If u and v are not already adjacent, adding the edge (u, v) creates a cycle in which all edges but (u, v) belong to G. Thus, there is a path from u to v, and since u and v were chosen arbitrarily, G is connected.
(1): Suppose that G is acyclic but that if any edge is added to E, a cycle is created. We must show that G is connected. Let u and v be arbitrary vertices in G. If u and v are not already adjacent, adding the edge (u, v) creates a cycle in which all edges but (u, v) belong to G. Thus, there is a path from u to v, and since u and v were chosen arbitrarily, G is connected. 5.5.2 Rooted and ordered trees
 y, then y is a proper ancestor of x and x is a proper descendant of y. The subtree rooted at x is the tree induced by descendants of x, rooted at x. For example, the subtree rooted at node 8 in Figure 5.6(a) contains nodes 8, 6, 5, and 9.
y, then y is a proper ancestor of x and x is a proper descendant of y. The subtree rooted at x is the tree induced by descendants of x, rooted at x. For example, the subtree rooted at node 8 in Figure 5.6(a) contains nodes 8, 6, 5, and 9.
Figure 5.6 Rooted and ordered trees. (a) A rooted tree with height 4. The tree is drawn in a standard way: the root (node 7) is at the top, its children (nodes with depth 1 ) are beneath it, their children (nodes with depth 2) are beneath them, and so forth. If the tree is ordered, the relative left-to-right order of the children of a node matters; otherwise it doesn't. (b) Another rooted tree. As a rooted tree, it is identical to the tree in (a), but as an ordered tree it is different, since the children of node 3 appear in a different order.
5.5.3 Binary and positional trees
 contains no nodes, or
contains no nodes, or is comprised of three disjoint sets of nodes: a root node, a binary tree called its left subtree, and a binary tree called its right subtree.
is comprised of three disjoint sets of nodes: a root node, a binary tree called its left subtree, and a binary tree called its right subtree.
Figure 5.7 Binary trees. (a) A binary tree drawn in a standard way. The left child of a node is drawn beneath the node and to the left. The right child is drawn beneath and to the right. (b) A binary tree different from the one in (a). In (a), the left child of node 7 is 5 and the right child is absent. In (b), the left child of node 7 is absent and the right child is 5. As ordered trees, these trees are the same, but as binary trees, they are distinct. (c) The binary tree in (a) represented by the internal nodes of a full binary tree: an ordered tree in which each internal node has degree 2. The leaves in the tree are shown as squares.


Figure 5.8 A complete binary tree of height 3 with 8 leaves and 7 internal nodes.
Exercises
 7, there exists a free tree on n nodes such that picking each of the n nodes as a root results in a different rooted tree.
7, there exists a free tree on n nodes such that picking each of the n nodes as a root results in a different rooted tree. V such that there exists a unique path from v0 to every vertex v
V such that there exists a unique path from v0 to every vertex v  V. Prove that the undirected version of G forms a tree.
V. Prove that the undirected version of G forms a tree. lg n
lg n .
. x w(x)
x w(x)  1, where the sum is taken over all leaves x in T. (This is known as the Kraft inequality.)
1, where the sum is taken over all leaves x in T. (This is known as the Kraft inequality.)Problems
 {0, l, . . . , k -1} such that c(u)
{0, l, . . . , k -1} such that c(u)  c(v) for every edge (u, v)
c(v) for every edge (u, v)  E. In other words, the numbers 0, 1, . . . , k - 1 represent the k colors, and adjacent vertices must have different colors.
E. In other words, the numbers 0, 1, . . . , k - 1 represent the k colors, and adjacent vertices must have different colors. colors.
colors. 2 people, there are two people with the same number of friends in the group.
2 people, there are two people with the same number of friends in the group. 3n/4 and |B|
3n/4 and |B|  3n/4.
3n/4. n/2
n/2 and |B| =
and |B| =  n/2
n/2 .
.Chapter notes


