

 CHAPTER 1: BASIC CONCEPTS
CHAPTER 1: BASIC CONCEPTS


 CHAPTER 1: BASIC CONCEPTS
CHAPTER 1: BASIC CONCEPTS
The collections of data you work with in a program have some kind of structure or organization. No matter how complex your data structures are, they can be broken down into two fundamental types: contiguous and non-contiguous.
In a contiguous structure, items of data are kept together in memory (either in RAM or in a file). An array is an example of a contiguous structure, since each element in the array is located next to one or two other elements. In contrast, items in a non-contiguous structure are scattered in memory, but are linked to each other in some way. A linked list is an example of a non-contiguous data structure. Here, the nodes of the list are linked together using pointers stored in each node. Figure 1.1 illustrates the difference between contiguous and non-contiguous structures.
Contiguous structures can be broken down further into two kinds: those that contain data items of all the same size, and those where the sizes may differ. Figure 1.2 shows examples of each kind. The first kind we'll call arrays. Figure 1.2(a) shows an example of an array of numbers. In an array, each element is of the same type, and thus has the same size.
The second kind of contiguous structure we'll call structs, because they can be defined using the C++ struct keyword. Figure 1.2(b) shows a simple struct consisting of a person's name and age. In a struct, elements may be of different types, and thus may have different sizes. For instance, a person's age can be represented with a simple integer that occupies perhaps two bytes of memory. But his or her name, represented as a string of characters, may require many bytes, and may even be of varying length.
C++ allows you to represent arrays and structs using built-in language features. For example, here's how the structures in Figure 1.2 could be coded in C++:
Coupled with the atomic types (that is, the single data-item built-in types such as integers, floats, and pointers), arrays and structs provide all the "mortar" you need to build more exotic forms of data structures, including the non-contiguous forms you are about to see.
Note The contiguous structures we call structs can be defined with the C++ class and union keywords, as well as with the struct keyword.
Non-contiguous structures are implemented as a collection of data items, called nodes, where each node can point to one or more other nodes in the collection. The simplest kind of non-contiguous structure is a linked list, as shown in Figure 1.3(a). The nodes of a linked list might be defined in this way:
Since this node has two pointers, it's called a doubly-linked list node. If you had just one pointer per node serving as, for example, next pointers, the node would be a singly-linked list node.
A linked-list represents a linear, one-dimensional type of non-contiguous structure, where there is only the notion of backwards and forwards. A tree, such as the one shown in Figure 1.3(b), is an example of a two-dimensional non-contiguous structure. Here, there is the notion of up and down, and left and right. In a tree, each node has only one link that leads into the node, and links can only go down the tree. The most general type of non-contiguous structure, called a graph, has no such restrictions. Figure 1.3(c) is an example of a graph.
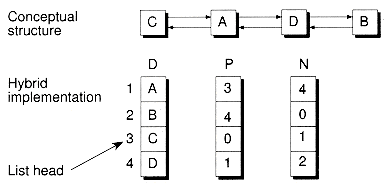
It's not uncommon for the two basic types of structures to be mixed into a hybrid form--part contiguous and part non-contiguous. For example, Figure 1.4 shows how to implement a doubly-linked list using three parallel arrays, possibly stored apart from each other in memory. The array D contains the data for the list, whereas the arrays P and N hold the previous and next "pointers." The pointers are actually nothing more than indexes into the D array. For instance, D[i] holds the data for node i, and P[i] holds the index to the node previous to i, which may or may not reside at position i - 1. Likewise, N[i] holds the index to the next node in the list.
The design of a data structure involves more than just its organization. You also need to plan for the way the data will be accessed and processed--that is, how the data will be interpreted. The previous section showed how three parallel arrays can be interpreted as implementing a linked list. Actually, all of the non-contiguous structures that we introduced--including lists, trees, and graphs--can be implemented either contiguously or non-contiguously. Likewise, the structures that are normally treated as contiguous--arrays and structs--can also be implemented non-contiguously.
Why this seeming paradox? The problem is that the notion of a data structure in the abstract needs to be treated differently from whatever is used to implement the structure. The abstract notion of a data structure is defined in terms of the operations we plan to perform on the data.
For example, the tree structure we provided in Figure 1.3(b) is called a binary tree, since each node has two children. We could define a binary tree node as follows:
Compare this definition with the one we provided earlier for a doubly-linked list node. You'll notice that the two types of nodes have the same memory layout. However, we've given two completely different interpretations of this layout. The difference lies in how we expect to be processing the data. With doubly-linked list nodes, we expect to be doing list-type operations, such as Next( ) and Prev( ). With binary tree nodes, we expect to use operations such as left( ) and Right( ).
Taken to its logical conclusion, considering both the organization of data and the expected operations on the data, leads to the notion of an abstract data type. An abstract data type is a theoretical construct that consists of data as well as the operations to be performed on the data.
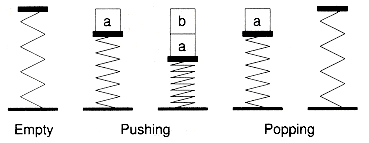
A stack is a typical example of an abstract data type. Items stored in a stack can only be added and removed in a certain order--the last item added is the first item removed. We call these operations pushing and popping, which are illustrated in Figure 1.5. In this definition, we haven't specified how items are stored on the stack, or how the items are pushed and popped. We've only specified the valid operations that can be performed.
Of course, to be useful, an abstract data type (such as a stack) has to be implemented, and this is where data structures come into play. For instance, we might choose the simple data structure of an array to represent the stack, and then define the appropriate indexing operations to perform pushing and popping. C++ allows you to create user-defined types to implement abstract data types, as you'll see next.
CIasses: User-Defined Data Types
C++ provides an elegant way to both define and implement abstract data types (although the term user-defined types may be more appropriate), through the use of the class, struct, and union keywords. (The structs we declared earlier were simple forms of classes.) For example, here's how we might define a stack of integers in C++:
This code defines a Stack type and specifies a particular implementation for it. The function headers in the public portion of the class define the abstract operations that can be performed on the stack. The function headers provide the interface to the data and indicate what operations are expected to be performed on the data. The function bodies, along with the private data, provide the implementation. Of course, this implementation is only one of many possibilities. We could, for instance, use a linked-list to store the stack elements. The "guts" of the class would change accordingly, but the interface would remain the same.
The ability to merge the structure of a data type with the specifications that describe how to operate on that data, through classes, marks the departure of C++ programming from C programming. The class construct allows us to easily create more than one instance of the data type. These instances are called objects. For example, if we declare a variable of type Stack, we've created a Stack object:
A whole new style of programming has evolved around using objects, and in fact is called object-oriented programming (OOP). For a discussion of OOP principles, see the references. We'll be indirectly using OOP constructs throughout this book. But whether or not we use OOP to implement data structures is a side issue. The focus here is on the data structures themselves.
Probably the most important process in designing a program involves choosing which data structures to use. The choice depends greatly on the type of operations you wish to perform. We can explore the fundamental issues for this decision-making process at a high level by examining the tradeoffs between contiguous and non-contiguous structures.
Suppose you have an application that uses a sequence of objects, where one of the main operations is to delete an object from the middle of the sequence. Here's how code might be written to perform deletion for an array of integers:
This function shifts toward the front all elements that follow the element at position posn. This shifting involves data movement that, for integer elements, isn't too costly. However, suppose the array stores large objects, and lots of them. In this case, the overhead for moving data becomes high. The problem is that, in a contiguous structure, such as an array, the logical ordering (the ordering that we wish to interpret our elements to have) is the same as the physical ordering (the ordering that the elements actually have in memory).
If we choose a non-contiguous representation, however, we can separate the logical ordering from the physical ordering and thus change one without affecting the other. For example, if we store our collection of elements using a doubly-linked list (with previous and next pointers), we can do the deletion without moving the elements. Instead, we just modify the pointers in each node.
Using the doubly-linked list Node structure we gave earlier, here's how we can rewrite the Delete( ) function:
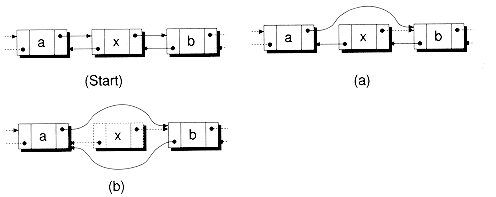
The process of deleting a node from a list is independent of the type of data stored in the node, and can be accomplished with some simple "pointer surgery" as illustrated in Figure 1.6. Since very little data is moved during this process, the deletion using linked lists will often be faster than when arrays are used.
It may seem that linked lists are superior to arrays. But is that always true? There are tradeoffs. Our linked lists yield faster deletions, but they take up more room because they require space for two extra pointers per element.
One way to evaluate the effectiveness of one data structure over another is to consider their space complexity functions, which measure their respective space
overhead. The complexity function for many data structures is linear, and can be written as:
Here, n represents the number of objects being stored, a is the number of memory cells used per object, and b is the number of memory cells of overhead that's independent of how many objects are stored. For example, suppose you have an array of n elements, along with a number that indicates the length of the array. Suppose also that the memory cells are expressed in units of words, with each array element requiring two words and the array length requiring one word. The complexity function could then be written as:
Compare this complexity with that of using a linked list. For a list of n objects, you not only have the space required by the objects themselves, but also space for the prev and next pointers. Assuming that each pointer requires one word, and that we again use a length indicator of one word, the following complexity function is obtained:
These functions illustrate mathematically what we concluded in the previous section: that linked lists have more space overhead than arrays.
Complexity functions can also be used on algorithms as well. Here, the functions are usually expressed in time units, with n representing the number of items to process. Consider an array-printing algorithm, shown in the following code:
For this algorithm, a step could be defined as the printing of one element. If n elements are in the array, there are n steps, and the time complexity of the algorithm can be written as the linear function:
Here, a is some constant multiplier that represents the time required to execute each step, perhaps in units of seconds, or in machine cycles. The constant b represents the setup time required to start the algorithm and to stop it.
While the time complexity function just given is linear, not all time complexities are linear. For example, the binary search trees of Chapter 10 can be searched with a logarithmic time complexity of:
For large n, log2n is much smaller than n. If n is one million, log2n is approximately 20. This result is significant. It means we can search through one million nodes in 20 steps, rather than the half-million steps needed for an array or linked list (assuming randomly ordered elements). This points out in a rather strong way how important it is to choose a data structure that matches the operations to be performed.
Since a linear function is so radically different from a logarithmic one, the constant terms and multipliers become less important when comparing the functions. In fact, time complexities are often expressed with the least significant terms dropped. For example, in a linear function, we say that the function is proportional to n. This proportionality is often denoted using what is called the big-Oh notation. For instance:
This statement is read "t(n) is order n." If the time complexity were a logarithmic function, we would write:
and say that the function is order logn. If the time complexity were quadratic, as is the case in a simple nested for loop, we would write:
and say that the function t(n) is order n2.
Using the big-Oh notation for space complexities is less meaningful, because most data structures are order n in space complexity. Thus, the constant terms and multipliers become very important in comparisons.
Note For a complete discussion of the big-Oh notation, see the companion volume [Flamig 93].
Choosing an efficient algorithm or data structure is just one part of the design process. Next, we'll look at some design issues that are broader in scope. If you think that many of these issues are nothing more than common sense, you're right. However, it's easy to get caught up in the technical gadgetry of a sophisticated program, and sometimes our common-sense reasoning gets lost.
There are three basis design goals that you should strive for in a program:
1. Try to save time.
2. Try to save space.
3. Try to save face.
In almost all situations, a program that runs faster is a better program, so saving time is an obvious goal. Likewise, a program that saves space over a competing program is considered desirable. However, even the fastest, most memory efficient program is a bad one if it doesn't work. You want to "save face" by preventing your program from locking up or generating reams of garbled data.
These three design goals are often mutually exclusive. The classic tradeoff involves speed versus space. Implementing a faster algorithm generally involves using more memory. For example, consider the tradeoffs involved in maintaining a sorted collection using a linked list versus an array. You saw where a linked list approach can be generally faster, but requires more memory to store extra pointers in each element. The extra pointers are used to save time in rearranging the elements.
The time/space tradeoff works in reverse, as well. Consider a database program that uses a paging scheme to keep memory requirements fixed, even for large databases. Instead of loading all records into memory, a small cache of, let's say, 50 records is used, and records are paged in and out of this cache as the database is accessed. While this strategy does keep memory requirements at a minimum, it slows down access to the records, due to the page shuffling that takes place.
You can liken the time-space tradeoff to the situation of a wood sculptor forced to work in a small, crowded room. As the sculptor chips away at his or her masterpiece, the chips pile up and soon begin to interfere with the work in progress. The sculptor must frequently stop and clear the chips away. If the room were larger, less time would be spent clearing the chips away. Likewise, programs that have an adequate amount of memory to work with are likely to be faster; less time is spent rearranging the contents of memory in order to keep working. In our database example, a lot of time is spent shuffling records in and out of memory. This activity could be eliminated if enough memory were available to store all the records in memory.
Tradeoffs also exist between saving time or space and maintaining the resulting code. In many cases, the most efficient algorithms are also the most complicated, since smarter code is needed to make the algorithms perform at their peak. Unfortunately, the more complicated the code, the more difficult it is to fix, modify, and port to other environments. You might actually be better off taking a performance hit and using simpler code instead.
Although it doesn't happen often, you can sometimes get lucky, and make your code faster, tighter, and easier to maintain--all at the same time. An example of this is the use of inline functions in C++. Used properly, inline functions can save you time and space by eliminating function call overhead. And inline functions can make your code easier to maintain by encapsulating the details of the functions (even if those details are rather brief).
Balancing the three main design goals makes programming more of an engineering art than an exact science because a large number of factors--many difficult to quantify--come into play. The next section outlines some design principles to help you perform this balancing act.
Unless your job is to be theorist, you want to be practical in your designs. As a programmer, you are being paid to produce, a fact that you should never lose sight of. Here are some practical design principles to keep you on the right track. Many of these principles are related to each other, and some are simply paraphrases of others.
Use simple, direct designs whenever possible. For instance, if you need to store a small list of numbers, don't get carried away by using some massive set of general purpose collection classes. A simple array will do just fine.
This doesn't mean you shouldn't strive to make your designs reusable and robust. But you should temper your eagerness to write, for example, the ultimate collection class, by asking yourself: "Is this really warranted? Will I (or someone else), be able to make changes to this code later on? What's the purpose of my activities? Is it my goal to write a general-purpose set of routines, or am I trying to solve just this one problem?"
An example of this principle is discussed in Chapter 10. There, we discuss the possibility of using a threaded tree over an ordinary tree, where each node has an extra pointer back to its parent. This parent pointer represents overhead that's incurred in every node (so it's type a overhead). The reason for using parent pointers is to simplify the code. But it might be better to have slightly more complex code, eliminating the parent pointers, and thus be able to use type b overhead instead of type a overhead.
It's interesting to note that Design Principle 8 permeates the design of the C++ language itself. While C++ adds object-oriented programming capabilities to C, you never pay for these capabilities when coding straight C without objects. Contrast this to the design of Smalltalk, where you are forced to pay for the overhead of using objects, regardless of whether you actually need to use objects to accomplish the task at hand.
In this chapter, we've reviewed the basic concepts behind data structures, and have given a set of common-sense principles that apply to all designs. In Chapters 2 and 3 we'll begin to focus on more specific principles as they apply to designing code in C++, with data structures particularly in mind.
Figure 1.1 Contiguous and non-contiguous structures compared.
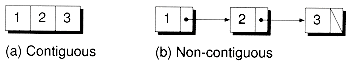
Contiguous Structures
int array[3];
struct personnel_data {int age;
char name[80];
};
Figure 1.2 Examples on contaguous structures.
int arr[3] = {1, 2, 3}; struct customer_data { int age;
char name[80];
} ;
customer_data billy = {21, "Billy the Kid"} ;
(a) Array

(b) Struct
Non-Contiguous Structures
struct Node { // A node storing an integerint data; // The node data
Node *prev; // Pointer to previous node
Node *next; // Pointer to next node
};
Hybrid Structures
Figure 1.3 Examples of non-contiguous structures.
(a) Linked list
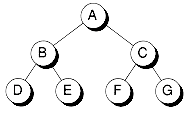
(b) Tree
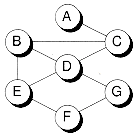
(c) Graph
TREATING DATA STRUCTURES IN THE ABSTRACT
Figure 1.4 A doubly-linked list via a hybrid data structure.
struct Node { // A binary tree node holding integer dataint data; // Node data
Node *left; // Left child of node
Node *right; // Right child of node
};
Figure 1.5 A push-down stack.
CIasses: User-Defined Data Types
class Stack {private:
int data[10]; // Our stack can hold 10 items
int top; // Current "top" of stack
public:
Stack( ) { top = 0; }Push(int a) { data[top++] = a; }int Pop( ) { return data[-top]; }};
Stack Mystack; // Mystack is a Stack object
SELECTING A DATA STRUCTURE TO MATCH THE OPERATION
void Delete(int *seq, int &n, int posn)
// Delete the item at posn from an array of n elements
{if (n) {int i = posn;
n-;
while(i<n) seq[i] = seq[i+1];
}
return;
}
void Delete(Node *seq, int posn)
// Delete the item at posn from a list of elements
{int i = posn;
Node *q = seq;
while(i && q) {i-; q = q->next;
}
if (q) {// Not at end of list, so detach p by making previous
// and next nodes point to each other
Node *p = q->prev;
Node *n = q->next;
if (p) p->next = n;
if (n) n->prev = p;
}
return;
}
Complexity Functions
Figure 1.6 Detaching a node from a list.
s(n)=an+b.
s(n)=2n+1.
s(n)=4n+1.
int i;
for(i = 0; i<n; i++) cout << a[i] << ' ';
cout << '\n';
t(n)=an+b.
t(n)=alog2n+b.
t(n)=O(n).
t(n)=O(logn)
t(n)=O(n2)
PRACTICAL DESIGN ISSUES
Three Design Goals
Some Design Principles
 Design Principle 1. Maintain the viewpoint of a practitioner. You have some programming task to accomplish. Your job is, first and foremost, to get the program working. Use whatever techniques are necessary to get the program working, no matter how inelegant those techniques may seem--that is, of course, unless an elegant solution is readily apparent and easily implemented, or if the alternatives are clearly inadequate. Try incorporating more elegant techniques only after the program is working, and only if it's warranted. For example, are you going to be using this program for years to come, or only once or twice?
Design Principle 1. Maintain the viewpoint of a practitioner. You have some programming task to accomplish. Your job is, first and foremost, to get the program working. Use whatever techniques are necessary to get the program working, no matter how inelegant those techniques may seem--that is, of course, unless an elegant solution is readily apparent and easily implemented, or if the alternatives are clearly inadequate. Try incorporating more elegant techniques only after the program is working, and only if it's warranted. For example, are you going to be using this program for years to come, or only once or twice? Design Principle 2. "There is no such thing as a complex solution." This quote from a colleague (see [Mohle 93]) sums up what is wrong with many programs today. A design that's too complex is no solution at all, since it may not be capable of being implemented (perhaps it takes too much memory), and may not be capable of being maintained, (and thus riddled with bugs). Chances are that a simpler, more elegant design is waiting out there in the ether for you to discover--if you just spend more time in the design phase.
Design Principle 2. "There is no such thing as a complex solution." This quote from a colleague (see [Mohle 93]) sums up what is wrong with many programs today. A design that's too complex is no solution at all, since it may not be capable of being implemented (perhaps it takes too much memory), and may not be capable of being maintained, (and thus riddled with bugs). Chances are that a simpler, more elegant design is waiting out there in the ether for you to discover--if you just spend more time in the design phase. Design Principle 3. Don't over-generalize. Many books on object-oriented programming show how to build general-purpose collection classes. While there is nothing wrong with this per se, it's easy to overdo it. General- purpose code tends to be less efficient than code written specifically for the task at hand, since more cases must be handled. Ironically, the more flexible your code is, the more difficult it can be to maintain--the opposite of what you might expect!
Design Principle 3. Don't over-generalize. Many books on object-oriented programming show how to build general-purpose collection classes. While there is nothing wrong with this per se, it's easy to overdo it. General- purpose code tends to be less efficient than code written specifically for the task at hand, since more cases must be handled. Ironically, the more flexible your code is, the more difficult it can be to maintain--the opposite of what you might expect! Design Principle 4. General-purpose code is not always the most reusable. This rule may seem at first like a paradox. But consider this: code that is very general purpose tends to be bloated and inefficient, due to the need to handle many cases. If the code is too bloated, you may not want to include it in your application. So it's not very reusable, is it? A surprising number of commercial toolkits suffer from this problem. One test that you can use on the objects you design is to ask yourself the following question: "Would I want to incorporate ten of these objects into another object?" This question will force you to think about how streamlined you've made your objects.
Design Principle 4. General-purpose code is not always the most reusable. This rule may seem at first like a paradox. But consider this: code that is very general purpose tends to be bloated and inefficient, due to the need to handle many cases. If the code is too bloated, you may not want to include it in your application. So it's not very reusable, is it? A surprising number of commercial toolkits suffer from this problem. One test that you can use on the objects you design is to ask yourself the following question: "Would I want to incorporate ten of these objects into another object?" This question will force you to think about how streamlined you've made your objects. Design Principle 5. Follow the 80-20 rule. This rule comes in many variations, including this one: in many programs, approximately 80 percent of the execution time is spent in 20 percent of the code. Few designs work well in all situations, so make your designs work well for the portion of code that's used most often. For the remaining code, the performance may suffer, but as long as your design doesn't totally stop working or produce the wrong results, don't worry about it too much. Of course, if you know a design that works well 100 percent of the time, and that design is cost-effective, by all means use it!
Design Principle 5. Follow the 80-20 rule. This rule comes in many variations, including this one: in many programs, approximately 80 percent of the execution time is spent in 20 percent of the code. Few designs work well in all situations, so make your designs work well for the portion of code that's used most often. For the remaining code, the performance may suffer, but as long as your design doesn't totally stop working or produce the wrong results, don't worry about it too much. Of course, if you know a design that works well 100 percent of the time, and that design is cost-effective, by all means use it! Design Principle 6. Design first, then optimize. As programmers, we've all made the mistake of trying to write and optimize code before we've even considered the design choices. Before optimizing a data structure, for instance, ask yourself if there is perhaps a better choice. Choosing a good data structure can make much more difference than merely optimizing the one you already have. For instance, no matter how clever you are in optimizing a linked list for searching a large number of records, a balanced binary tree is likely to perform much better, even without any optimization.
Design Principle 6. Design first, then optimize. As programmers, we've all made the mistake of trying to write and optimize code before we've even considered the design choices. Before optimizing a data structure, for instance, ask yourself if there is perhaps a better choice. Choosing a good data structure can make much more difference than merely optimizing the one you already have. For instance, no matter how clever you are in optimizing a linked list for searching a large number of records, a balanced binary tree is likely to perform much better, even without any optimization. Design Principle 7. Try to get the most leverage out of any overhead you must add. Writing robust code often entails writing smarter code. And smarter code usually has more overhead associated with it. The issue is where this overhead is placed. For instance, consider the linear space complexity function s(n) = a n + b. The terms a and b represent overhead. The overhead represented by a is multiplied n times (where n is the number of objects stored), so you obviously want to avoid adding overhead there if you can. The overhead represented by b is much more benign since it's just a constant factor. Thus, strive to add type b overhead rather than type a overhead.
Design Principle 7. Try to get the most leverage out of any overhead you must add. Writing robust code often entails writing smarter code. And smarter code usually has more overhead associated with it. The issue is where this overhead is placed. For instance, consider the linear space complexity function s(n) = a n + b. The terms a and b represent overhead. The overhead represented by a is multiplied n times (where n is the number of objects stored), so you obviously want to avoid adding overhead there if you can. The overhead represented by b is much more benign since it's just a constant factor. Thus, strive to add type b overhead rather than type a overhead. Design Principle 8. You shouldn't have to pay for something you aren't going to use. Consider using a general-purpose collection class when all you really want is a simple array. Why should you pay for the extra overhead? Yet many poorly designed libraries want you to do just that.
Design Principle 8. You shouldn't have to pay for something you aren't going to use. Consider using a general-purpose collection class when all you really want is a simple array. Why should you pay for the extra overhead? Yet many poorly designed libraries want you to do just that. SUMMARY