In a B-tree, one tree node can be made to correspond to a page. Because binary nodes aren't usually large enough to take up one page, a B-tree node stores multiple keys and branches. A beneficial side effect of such multi-way nodes is that the height of the tree can be smaller than that of a binary tree. Using multi-way nodes also makes it easier to balance the tree. Both of these properties lead to even faster searching than can be obtained by using disk paging alone.
This chapter first shows the data structures used to implement B-trees, followed by the operations on B-trees in order of complexity--from searching to inserting and deleting. Since B-trees were designed with files in mind, we'll make our B-trees file-based, using the classes developed in Chapter 13 for this purpose.
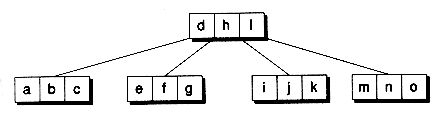
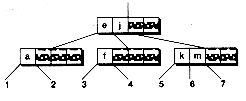
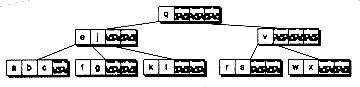
B-trees are classified by their order, which refers to the maximum number of branches in a node. For example, in a B-tree of order 4, each node can have up to 4 branches. Corresponding to these branches are 3 keys that help determine which branch to take during a se arch. In general, a B-tree of order m has nodes with up to m branches and m-1 keys. Note that the order specifies the maximum number of branches. A node may have fewer branches than the maximum. Figure 14.1 shows a B-tree of order 4, with all nodes full. You've seen B-trees of order 4 before. They are the 2-3-4 trees we introduced in Chapter 11. (We've drawn them differently in this chapter, however.)
Not all multi-way trees are B-trees. A multi-way tree is considered to be a B-tree only if it is balanced. In the classical definition of a B-tree of order m, the balance is achieved by maintaining the following properties:
Note Some texts define the order of a B-tree differently than we have here. In the alternative definition, a B-tree of order d has nodes with a maximum of 2d keys and 2d+1 branches. Implied in this definition is that the maximum number of keys is always even, and the minimum number of keys in a non-root node is d. In our definition, the maximum number of keys can be odd.
As was the case with 2-3-4 trees, the key to efficient B-trees lies in maintaining the two properties just mentioned. Doing so will yield balanced trees that are reasonably compact.
At the heart of B-trees are the multi-way nodes that make up the trees. Multi-way nodes are essentially generalizations of binary nodes. Rather than show generic template-based nodes in this chapter, we'll show a direct design that's typical of what might be used in practice. (You're probably tired of seeing templates, anyway.)
For keys, we'll use a character string of some maximum size. Stored with each key is a long integer that represents the associated data. While in some applications you might be able to fit all of your data in the long integer, the intent is for this variable to be the file address of the data--as stored elsewhere. For example, you might store the B-tree in one file that serves as an index to another file holding the actual data.
The following B-tree class, and its associated data structures, can be used to set up a B-tree:
Complete code for the B-tree class is given on disk in the files btree.h and btree.cpp test program is provided in the file btreet1.cpp.
Since the B-tree class is file based, it has numerous file-management functions, such as Connect( ), Disconnect( ), Create( ), Open( ), Close( ), and Flush( ), among others. These functions allow multiple B-trees to be stored in a single file. Each B-tree has a header, defined in B-treeHeader, which points to the root node of the tree, and stores some other pertinent data used mostly for testing. The headers are meant to be stored in the static data area of the file, although their exact locations are user defined. Unfortunately, we don't have sufficient space to describe the file-management functions in detail. Refer to the disk for more information.
Each B-tree has its own cache of buckets that store Mnodes. Also, a Coptr to the root of the tree is kept for easy access. The constructor is used to initialize these members, as well as to set the file manager pointer to null at the outset:
The following Search( ) routine can be used to search a B-tree. The searching algorithm is very similar to that used for a binary tree, except now there are more keys and branches to choose from. The Mnode Search( ) function is at the heart of the search. Since the tree is file based, note how Coptrs are used instead of Mnode pointers:
The Search( ) function assumes you've set up an entry with the key field defined. When a match is found, the data field is filled in with the appropriate value. This example calls Search( ):
A companion function, FullSearch( ), compares both the key and data fields of the entry. This function is similar to search, except the call to Mnode's Search( ) function is replaced by a call to Mnode's FullSearch( ) function.
In Chapter 11, we described how to insert nodes into a 2-3-4 tree. The method involves inserting a new entry into a leaf and, if the appropriate leaf is full, it is split in two, with node splits propagating up the tree as necessary. Not surprisingly, a similar method is used for general B-trees. The only drawback is that it isn't possible to define an efficient, single-pass, top-down algorithm for general B-trees. (At least, nobody has come up with such a method.) Instead, we'll use a two-pass recursive algorithm.
First, we walk down the tree until we either find a matching key and data pair (which means we have a duplicate entry--not allowed) or we hit a leaf node. At this point, we attempt to insert the new entry into the leaf. If the leaf isn't already full, we can simply do the insertion. Otherwise, the node is split in half. For this technique to work, we must send one of the entries up the tree to be inserted into the parent. We always use the median entry (as defined in sorted order) for this purpose. Note that the median may actually be the entry we tried to insert in the first place.
If the parent is full and can't handle the median entry, the parent must be split as well, with the parent's median entry (which may be different from the original median entry) sent further up the tree. Eventually, the root node might have to be split in half, and a new root created to contain the median entry. Due to the bottom-up node splitting, B-trees always grow at the root. This keeps the leaves all at the same level, and results in a well-balanced tree.
Figure 14.3 shows some insertions when the corresponding leaf nodes aren't full. Figure 14.4 shows a node being split to accommodate a new key. Figure 14.5 shows an example of two splits occurring, one which involves growing a new root.
The insertion algorithm is partitioned into two functions. The Add( ) function is the top-level "driver" function. It constructs an entry to be searched, and then calls the recursive Insert( ) function. This latter function walks down to a leaf node, inserts the entry there, and then propagates any splits up the tree as the recursion unwinds. Function return status codes are used to control the recursion.
When Insert( ) returns a NODE_OVERFLOW code, this means the node below was split, and the median entry is passed back for further processing.
Eventually, the top of the tree is reached, and the last call to Insert( ) is unwound. At this point, Add( ) checks to see if the node that was split was the root. If so, a new root is created, with the median entry passed back as the root's sole entry.
As you examine the Add( ) and Insert( ) routines, note how Coptrs allow us to write the routines almost as though we were working with trees in memory. The process isn't quite automatic, as we've explained in Chapter 13. For example, before a recursive call, we must release any Coptrs that might be bound--to prevent the cache from becoming full.
We must also remember to set the dirty bits for any nodes that might be modified. We've made it a convention to set dirty bits each time we modify a node, even though the dirty bits might already have been set due to prior modifications. With careful analysis, it's possible to optimize the setting of the dirty bits. But when you first write the code, the redundancy is well worth it. If you forget to set a dirty bit, the code will eventually fail, but the problem may remain undetected for a long time and may be difficult to locate.
As you might expect, deleting from a B-tree is much more involved than insertion. We use the same technique that's used for all search trees. When the entry to be deleted isn't in a leaf node, we replace the entry with its successor, and then delete the successor entry from its original home, which will always be a leaf node. Recall that, with red-black trees (and their 2-3-4 tree equivalents), even deleting from a leaf isn't always so simple. We must maintain the balance of the tree. The same applies to B-trees.
For B-trees, maintaining balance translates into ensuring that each non-root node is at least half full. (Notice that the splitting process just described for insertions does just that.) After deleting an entry from a leaf, we check to see whether the node still has the minimum required number of entries. If not, we must borrow an entry from some other node. The appropriate nodes to borrow entries from are the left and right siblings. We can't just simply move an entry from a sibling, however. We must maintain the order of the entries so that the tree can be searched properly. We can do this by first moving the sibling entry into the parent node, then moving the original parent entry into the node needing the entry.
This borrowing process is interesting because, in effect, we end up performing tree rotations that are the generalized versions of what we used for binary trees. Figure 14.6 illustrates both left and right rotations. When doing a left rotation, we always borrow the leftmost entry of the right sibling. In a right rotation, the rightmost entry of the left sibling is used.
When both the left and right siblings have entries to spare, it's arbitrary which sibling you borrow from. In the code we'll present later, we always choose the left sibling. In some cases, neither sibling has any extra entries. When this happens, we can combine the given node with one of the siblings. (Again, the choice is arbitrary.) This merging process involves an entry from the parent node as well.
Figure 14.7 illustrates two examples that merge a node with its left and right siblings. In this figure, we've assumed the nodes shown are in the middle of a B-tree. As we did with the red-black trees defined in Chapter 11, we've represented external nodes (which are subtrees that may be null) using links that go nowhere and that are labeled with numbers. These numbers help you to easily see how the links are re-arranged. Note that, in the case of a left merge, the original parent entry has its right link set to the left link of the right node. Thus, we don't lose track of any nodes below ones involved in the merge. Right-hand merges have a similar linking process.
When nodes are merged, we end up with one less entry in the parent node. It's possible for the parent to end up with too few entries, so it must borrow entries or merge with one of its siblings. This borrowing and merging may thus propagate up the tree. Note that it's legal for the root to have fewer than the minimum number of entries. But what if the root becomes empty due to a merge? In this case, the tree shrinks one level, with the new root being the node to the left of the old empty root. Figure 14.8 illustrates this process.
It's relatively easy to describe how deletions work in a B-tree, but it's another matter entirely to write code for deletions. We've split the task into six functions: Remove( ), Delete( ), RestoreBalance( ), RotateLeft( ), RotateRight( ), and Merge( ). The Remove( ) function is the "driver," which sets up the entry to delete and calls the recursive Delete( ) function. This latter function searches the tree for the entry to delete, using recursive calls to itself. When the entry is found, the tree is further traversed in search of the successor entry to use as the replacement. When the entry has been replaced, the function is recursively called again to delete the successor entry in its original leaf node.
The recursion bottoms out when an entry is to be deleted from a leaf node. At this point, the entry is removed from the node. Then, RestoreBalance( ) is called to do whatever rotation or merging is necessary to ensure that the node with the deleted entry has at least the minimum number of entries. As the recursion in Delete( ) unwinds, the merging is propagated up the tree as needed. Eventually, the program execution returns to the Remove( ) function. A test is made to see if the root node has become empty due to a merge that took place below it. If so, the root is removed from the tree and the node to the root's left becomes the new root. If the old empty root is the only node in the tree, it is left empty. Thus, we also have at least one node in the tree, even if it's empty.
Here are the six functions used for deletions:
The design we've just presented for B-trees is simple and basic. We "hard coded" the type of keys stored in the B-tree nodes as character strings. We also used global constants such as MAXKEYSIZE and NBR to size the nodes. These could obviously be made into template parameters, and it is possible to write a generic B-tree class that allows you to share the code for B-trees across all types of nodes.
For instance, you could build an abstract node class that doesn't know the order of the node, or the key types stored within it. Then, more type-specific template classes could be derived. However, it gets a little tricky to use the abstract nodes, since Coptrs are being used. Because the node types are parameters to Coptrs, the fact that one node type is derived from another does not mean that the corresponding Coptrs have any special base-to-derived relationship. The different Coptr classes remain siblings of the Coptrb class, and are otherwise not related. Thus, where you can use implicit derived-to-base type equivalence with ordinary node pointers, with Coptrs, you must do explicit type casting.
One problem with the B-tree design presented here: Fixed-length keys are used, which aren't desirable when the keys are character strings. A lot of wasted space results in the nodes when the keys aren't the maximum size. It's possible to design B-tree nodes that allow for variable-length keys, where each key occupies only as much room as needed in a node. As many keys as possible can be packed into each node. This means the nodes can have a variable number of keys and branches. The result is a variable order B-tree. In such a tree, we use half the size of the node as the criteria for minimum node size, rather than using half the number of keys.
Searching and inserting into a variable-order B-tree is about as simple as it is for trees with fixed orders. However, deletion is more complicated (as if it weren't complicated enough). With fixed-length keys, the rotation and merge operations are fairly straightforward. We can always guarantee that one key can take the place of another, because they all have the same size. With variable-length keys, such replacements can't be guaranteed. For example, if we attempt to do a rotation when the sibling key is larger than the parent key, theres no guarantee that the sibling key will fit in the parent node.
We designed the insertion and deletion routines using recursive functions. It's possible to use an explicit stack instead, and thus convert the recursion into iteration. Each stack element must have both a node pointer and an index representing which entry in the node we are on. If you use Coptrs for the node pointers, they must be released before putting them on the stack. Because the bucket pointers for released Coptrs will still be intact, there's a good chance that when you pop the Coptrs off the stack, you can quickly rebind them to their respective buckets.
There's an important advantage that results from using an explicit stack. You can have a built-in iterator, which allows you to move back and forth through the entries in the tree in sorted order. This feature is particularly handy in such applications as a customer contact list. For example, you can search for a customer record using the customer name, and then quickly scan back and forth through other customer records in sorted order.
For information about obtaining source code for a variable-order B-tree class with a built-in iterator, see the README file on disk.
In our B-tree design, we included "data" with each key. (Usually, this data is simply the file address of the real data record.) In some variations of B-trees, only the leaf nodes have data. The internal nodes only contain the keys to be used in the search process. These types of trees are sometimes called B+-trees. You can go one step further and, instead of storing the full keys in each node, you store only prefixes of each key, enough to guide the search process to the correct leaf node. Trees with these types of keys are often called prefix B-trees. For a discussion about some of these B-tree variants, see [Aoe 91].
B-trees, or variations of them, have become the data structures of choice for database applications. B-trees allow fast database searching, due to the ability to optimally size the nodes to the paging requirements of a file system, and due to the relative flatness that results by using multi-way nodes. By using a cache in conjunction with the B-tree nodes themselves, you can speed up the searching even more.
While B-trees were designed with files in mind, it's possible to use memory-based B-trees. However, you're probably better off using red-black trees for trees that totally reside in memory. That's because the larger nodes of a B-tree don't provide an advantage for memory-based designs. You must search sequentially through the entries of a node, looking for the appropriate branch to take. For nodes with many entries, this can become time-consuming. (With file-based trees, searching within a node is often masked by the relatively slower file access needed to retrieve the node.) Of course, you could use a binary search to find the appropriate location in the array of entries. However, you're not much better off than if you had simply used a binary tree.
PROPERTIES OF B-TREES
Except for the root node, all nodes must have at least (m-1)/2 keys and (m-1)/2 + 1 branches. This means all nodes except the root are roughly half full. For example, in an order 5 B-tree, all non-root nodes must have at least two keys. For an order 4 B-tree, the nodes must have at least one key. The leaves of the tree are always on the same level. MULTI-WAY NODES
Figure 14.1 A B-tree of order 4.
THE B-TREE CLASS
// Function return status codes
const int NODE_OVERFLOW = 2;
const int SUCCESS = 1;
const int FAIL = 0;
const int DUPLKEY = -1;
const int ALLOCERR = -2;
struct BtreeHeader { // Stored with every treelong root_addr;
unsigned order;
unsigned num_entries;
unsigned num_nodes;
int height;
};
class Btree { // Btree file classprotected:
FmgrPtr f; // File the Btree is connected to
long bh_addr; // Address of the Btree header
BtreeHeader bh; // Btree header
Cache<Mnode> cache; // Node cache
Coptr<Mnode> root; // Pointer to the root node
void ReadHdr( );
void WriteHdr( );
int Insert(Entry &e, Coptr<Mnode> t);
int Delete(Entry &e, Coptr<Mnode> t);
void RestoreBalance(Coptr<Mnode> p, int posn);
void RotateRight(Coptr<Mnode> p, int posn);
void RotateLeft(Coptr<Mnode> p, int posn);
void Merge(Coptr<Mnode> p, int posn);
static void PrintNode(Coptr<Mnode> &n);
static void PrintTree(Coptr<Mnode> t, int sp);
public:
Btree(int cs = 8);
~Btree( );
// File-management routines
int Connect(FmgrPtr &fptr, int create,
long bh_addr-sizeof(FmgrHeader));
void Disconnect( );
int Create(char *fname, long bh_addr=sizeof(FmgrHeader));
int Open(char *fname, Fmgr::AccessMode mode,
long bh_addr=sizeof(FmgrHeader));
void Flush(int clear=0);
void Close( );
int Search(Entry &e);
int FullSearch(const Entry &e):
int Add(char *k, long d=0);
int Remove(char *k, long d = 0);
int IsEmpty( ) const;
int IsOpen( ) const;
int OK( ) const;
int operator!( ) const;
operator int( ) const;
void ClearErr( );
void Statistics(int full);
void PrintTree( );
};
Btree::Btree(int cs)
// Create a Btree with a null file manager, and with a
// cache size of cs
: f(0), cache(cs), root(cache)
{}
SEARCHING A B-TREE
int Btree::Search(Entry &e)
// Search the tree for the first node having a matching
// entry (i.e., keys must match). If found, the data
// field of e is filled in. Returns SUCCESS or FAIL.
{Coptr<Mnode> t(root);
int rv, posn;
while(t) {rv = t->Search(e, posn); // Search node t, get back posn
if (rv == 0) { // Found a matche = t - >entry[posn]; // Causes the data to be filled in
return SUCCESS;
}
t = t -> Branch(posn); // No match, keep walking
}
return FAIL;
}
Entry e("look for me");if (mytree.Search(e) == SUCCESS) {cout << "Entry found, with data: " << e.data << '\n';
}
INSERTION INTO A B-TREE
Figure 14.3 Inserting into a B-tree without splits.
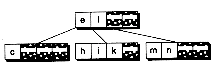
(a) Original tree
(b) After adding b
(c) After adding j
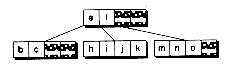
(d) After adding o
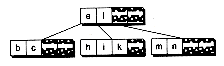
Figure 14.4 Inserting into a B-tree with a split.
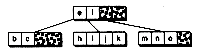
(a) Original tree
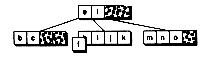
(b) Inserting f
(c) Node split in half
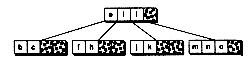
(d) Median inserted into parent
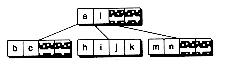
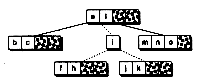
Figure 14.5 Propagating splits and growing a new root.
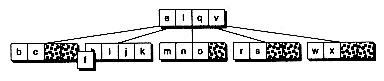
(a) Before inserting f and causing splits
(b) After two splits, including the root
int Btree::Add(char *k, long d)
// Creates a new entry with key k and data d, and attempts to
// add the entry to the tree. Returns SUCCESS, DUPLKEY, or
// ALLOCERR.
{Entry e(k, d);
int rv = Insert(e, root);
if (rv == NODE_OVERFLOW) { // Need to grow a new rootCoptr<Mnode> old_root(root);
new(root) Mnode;
if (root == 0) return ALLOCERR;
bh.num_nodes++: bh.height++;
bh.root_addr = root;
root->left = old_root;
root->InsEntry(e, 0);
rv = SUCCESS;
}
if (rv == SUCCESS) bh.num_entries++;
return rv;
}
int Btree::Insert(Entry &e, Coptr<Mnode> t)
// Recursive function that tries to insert entry e into subtree t.
// Returns SUCCESS, DUPLKEY, ALLOCERR, or NODE_OVERFLOW.
// If NODE_OVERFLOW, then e becomes the median_entry to pass
// back to t's parent.
{int rv, posn;
if (t == 0) {// We went beyond the leaves. Pretend that we've overflowed.
e.right = 0;
return NODE_OVERFLOW;
}
// Search the node t. If entry found, send back duplicate key error.
rv = t->FullSearch(e, posn); // Use both key and data
if (rv == 0) return DUPLKEY;
// Entry not found; go down to the appropriate leaf to store entry
Coptr<Mnode> child(t);
child = t->Branch(posn);
t.Release( ); // Prevents cache from filling up during recursion
rv = Insert(e, child); // Recursive call
// Back from recursion; see if we have an overflow
child.Release( ); // Prevents cache from filling up
if (rv != NODE_OVERFLOW) return rv;
// We have overflowed the node below us. See if we can
// insert the entry e (now the median) into node t.
posn++; // Move to the appropriate entry for insertion
if (!t->IsFull( )) { // Simply add entry to node tt->InsEntry(e, posn);
t->SetDirty( );
return SUCCESS;
}
else { // Need to split node t.// Create new node to be the right node. t will be the left node.
Coptr<Mnode> r(t);
new(r) Mnode;
if (r == 0) return ALLOCERR;
bh.num_nodes++;
// Move roughly half the nodes to the right node. If inserting
// entry into left node, we need to move the split position back
// one, so that when the median is taken, the split node will have
// enough entries.
int split_posn = NBR/2;
if (posn < split_posn) split_posn-;
t->Split(*r, split_posn);
t->SetDirty( );
// Determine where entry e should go
if (posn > split_posn) { // e goes to the right node// First entry of right node is the median
Entry median_entry = r->entry[0];
r->DelEntry(0);
// Insert e into its correct spot
r->InsEntry(e, posn-split_posn-1);
e = median_entry; // For passing up the tree
}
else if (posn < split_posn) { // e goes to the left nodet->InsEntry(e, posn); t->SetDirty( );
e = r->entry[0]; // Get median from the right
r->DelEntry(0);
}
// At this point, e is median entry to add to parent.
// Record what e's right pointer is going to be.
r->left = e.right;
e.right = r;
return NODE_OVERFLOW;
}
}
DELETING ENTRIES FROM A B-TREE
B-tree Rotations
Merging Nodes
Figure 14.6 B-tree rotations.
(a) Left rotation (borrowing from the right)
(b) Right rotation (borrowing from the left)
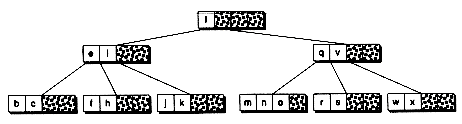
Figure 14.7 Merging B-tree nodes.
(a) Before merging with the left sibling
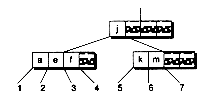
(b) After merge
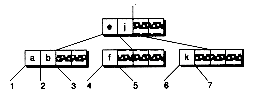
(c) Before merging with the right sibling
(d) After merge
The Deletion Functions
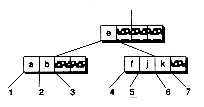
Figure 14.8 Shrinking a B-tree.
(a) Before merge
(b) After merge
(c) Final tree
int Btree::Remove(char *k, long d)
// Deletes entry having key k and data d from the tree.
// Returns SUCCESS, or FAIL if we couldn't find the entry.
{Entry e(k, d);
int rv = Delete(e, root);
if (rv == SUCCESS && root->IsEmpty( ) && bh.height > 1) {// We need to shrink the tree
Coptr<Mnode> p = root;
root = root->Branch(-1);
bh.root_addr = root;
bh.num_nodes-; bh.height-;
p.Delete( );
}
return rv;
}
int Btree::Delete(Entry &e, Coptr<Mnode> p)
// Recursive function that deletes entry e from the subtree
// with root p. Returns SUCCESS, or FAIL if we couldn't find
// the entry.
{Coptr<Mnode> t(p), s(p);
int rv, posn, sr;
sr = p->FullSearch(e, posn); // Search node p
t = p->Branch(posn); // Get ready to walk down the tree
if (sr == 0) {// p has entry to delete. Replace the entry with its
// successor, if there is one.
if (t) {s = t;
while(s->Branch(-1)) s = s->Branch(-1);
p->entry[posn] = s->entry[0];
p->Branch(posn) = t; // Remember to restore the branch
p->SetDirty( ); // Don't forget
// Now, using recursion, delete the successor entry.
// Release the coptrs in use, to keep cache from.
// filling up during the recursion, and to prevent
// dangling pointer exceptions
p.Release( );
Entry &se = s->entry[0];
s.Release( );
if (Delete(se, t) != SUCCESS)
excp->THROW(ASSERTERR); // We should have found the entry
}
else { // At a leaf, so the deletion is easyp->DelEntry(posn);
p->SetDirty( ); // Don't forget
bh.num_entries-;
}
rv = SUCCESS;
}
else {if (t) {// Walk down the tree, looking for entry
p.Release( ); // Keep cache from filling up on recursive call
rv = Delete(e, t);
}
else return FAIL; // Couldn't find said entry
}
if (rv == SUCCESS && t && t->IsPoor( )) {// The node below p doesn't have enough entries. We need to
// move some entries to it and thereby restore the balance.
t.Release( ); // To prevent dangling ptrs
RestoreBalance(p, posn);
}
return rv;
}
void Btree::RestoreBalance(Coptr<Mnode> p, int posn)
// Node down branch at position posn in node p has one too
// few entries. Give it an entry from either its left or right
// sibling, or perhaps just merge the node with a sibling.
{Coptr<Mnode> t(p);
if (posn == -1) {// We have no left sibling, so try the right sibling
t = p->Branch(0);
if (t->IsPlentiful( )) { // Can we borrow from the right?RotateLeft(p, 0); // Do so
}
else { // Right sibling has no spare entriest.Release( ); // To prevent dangling ptr errors
Merge(p, 0); // Merge with right node and parent entry
}
}
else if (posn == p->LastPosn( )) {// We have no right sibling, so try the left sibling
t = p->Branch(posn-1);
if (t->IsPlentiful( )) { // Can we borrow from the left?RotateRight(p, posn); // Do so
}
else { // Left sibling has no spare entries.t.Release( ); // To prevent dangling ptr errors
Merge(p, posn); // Merge with left node and parent entry
}
}
else {// We have both left and right siblings
t = p->Branch(posn-1);
if (t->IsPlentiful( )) { // Can we borrow from the left?RotateRight(p, posn); // Do so
}
else {t = p->Branch(posn+1);
if (t->IsPlentiful( )) { // Can we borrow from the right?RotateLeft(p, posn+1); // Do so
}
else {// Neither the left or right sibling has spare entries.
// Merge arbitrarily with the left node.
t.Release( ); // To prevent dangling ptr errors
Merge(p, posn); // Merging with the left
}
}
}
}
void Btree::RotateRight(Coptr<Mnode> p, int posn)
// Performs a "right rotation" using the entry at node p,
// position posn as the pivot point. Assumes p is not
// a leaf and that a left and right child exist.
// Also assumes right child isn't full, and that p and
// left child aren't empty.
{Coptr<Mnode> l(p), r(p);
r = p->Branch(posn); // Right child of p
l = p->Branch(posn-1); // Left child of p
// Move entry from parent p into rightmost entry of right node.
// This entry will have the old left branch of right node. (The
// left branch will be updated later.)
p->Branch(posn) = r->left; p->SetDirty( );
r->InsEntry(p->entry[posn], 0); r->SetDirty( );
// Now, move rightmost entry of the left node into p. This
// entry's branch becomes the right node's left pointer.
// Be sure to point entry to right node.
int last_posn = l->LastPosn( );
r->left = l->Branch(last_posn); r->SetDirty( );
l->Branch(last_posn) = r; l->SetDirty( );
p->entry[posn] = l->entry[last_posn]; p->SetDirty( );
l->DelEntry(last_posn); l->SetDirty( );
}
void Btree::RotateLeft(Coptr<Mnode> p, int posn)
// Does a "left rotation" using the entry at node p,
// position posn as the pivot point. Assumes p is not
// a leaf and that a left and right child exist.
// Also assumes left child isn't full, and that p and
// right child aren't empty
{Coptr<Mnode> l(p) , r(p) ;
r = p->Branch(posn) ; // Right child of p
l = p->Branch(posn-1) ; // Left child of p
// Move entry from parent p into leftmost entry of left node.
// This entry gets the left pointer of the right node.
p->Branch(posn) = r->left ; p->SetDirty( ) ;
l->Concatenate(p->entry[posn]) ; l->SetDirty( ) ;
// Now, move rightmost entry of the right node into p. Make
// sure this entry points to the right node. Also, we have
// a new left branch of the right node.
r->left = r->Branch(0) ;
r->Branch(0) = r ; r->SetDirty( ) ;
p->entry[posn] = r->entry[0] ; p->SetDirty( ) ;
r->DelEntry(0) ; r->SetDirty( ) ;
}
void Btree: :Merge(Coptr<Mnode> p, int posn)
// Merges the node on the branch left of the entry at position
// posn of node p with the entry of p, and the node on the
// branch to the right of the entry of p. Assumes posn in range.
{Coptr<Mnode> l(p) , r(p) ; // Ptrs to left and right children
r = p->Branch(posn) ; // Right child of p
l = p->Branch(posn-1) ; // Left child of p
// (1) Fix entry of p to point to left branch of r
// (2) Insert this into leftmost entry of l
// (3) Add all of r's entries
// (4) Delete entry from p, then delete r
p->Branch(posn) = r->left ; p->SetDirty( ) ;
l->Concatenate(p->entry[posn]) ; l->SetDirty( ) ;
l->Concatenate(*r) ; l->SetDirty( ) ;
p->DelEntry(posn) ; p->SetDirty( ) ;
r.Delete( ) ;
bh.num_nodes- ;
}
BEYOND BASIC B-TREES
SUMMARY