template<class TYPE>
struct Snode {
TYPE info; // Holds the data for the node
Snode<TYPE> *next; // Pointer to next node in the list
Snode(const TYPE &x);
void InsertAfter(Snode<TYPE> *n);
Snode<TYPE> *RmvNext();
};
The constructor initializes the info field by copying the parameter x and then sets the next pointer to zero. It's assumed that TYPE has a copy constructor or is a built-in type:
Figure 8.1 Singly-linked versus doubly-linked lists.
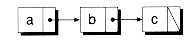
(a) Singly-linked list
(b) Doubly-linked list
template<class TYPE>
Snode<TYPE>::Snode(const TYPE &x)
: info(x)
{
next = 0;
}
Setting next to zero is optional, but it aids in constructing null-terminated lists--that is, lists whose last nodes have null next pointers.
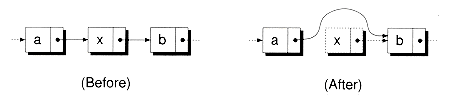
Inserting a node into a linked list is illustrated in Figure 8.2, and is implemented with the following InsertAfter( ) function:
Insertion works by copying the current code's next pointer into the next pointer of the new node, and then having the current node point to the new node. Here is an example that creates the list shown previously in Figure 8.1(a):
This code takes advantage of the fact that the constructor for Snode sets the next pointer to zero. Thus, the linked list is guaranteed to be null terminated. You'll notice that we built part of the list backwards because it's more efficient to add to the front of the list than to the back. (Later, we'll show you some ways to get around this.) Also, the first node was allocated statically, but the other nodes were allocated dynamically. It doesn't really matter how linked-list nodes are allocated. Later, we'll exploit that fact, implementing linked-lists through various memory allocation schemes.
Suppose you want to insert a node before another node. With singly-linked lists, this is awkward because you must scan the list from the beginning to get to the previous node. Assume that p starts out pointing to the front of a null-terminated list, and n is the node you wish to insert before the node q. Here are the necessary steps:
You may have noticed that it isn't possible to insert before the first node in the list. (Think about the case where q equals the intial value of p.) To solve this problem, you can incorporate a dummy header node at the front of the list. This node's only purpose is to provide a "handle" for the list. The info field is ignored. Here, we show another way to build the list shown previously in Figure 8.1a--this time, using a dummy header node (the header node isn't shown in Figure 8.1a):
Each InsertAfter( ) operation inserts before the previous first node of the list, starting with no first node.
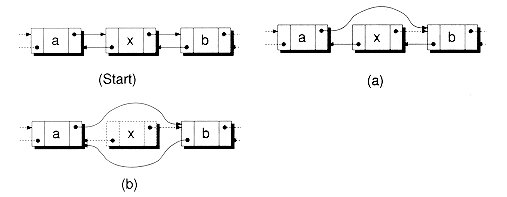
The complement to the InsertAfter( ) function is the following RmvNext( ) function, which, given a node, allows you to remove the node that follows it. Figure 8.3 illustrates the steps involved in removing a node from a singly-linked list.
Here's an example that shows how to remove and delete the first node of the list given previously:
Note that RmvNext( ) does not de-allocate the node, but rather just detaches the node from the list. The de-allocation is handled separately. Removing a node from a singly-linked list has the same awkwardness as inserting a node. Suppose you have a node q, and you wish to remove that node rather than the one that follows it. Here's how this can be done (assuming a null-terminated list with a header):
The removal involves m steps, where m is the position of q in the list. The awkardness of singly-linked lists can be alleviated by adding another link to each node, pointing to the previous node. We'll examine such doubly-linked nodes next.
Sample code for implementing a singly-linked list is given on disk in the file ch8_1 .cpp.
Here is a typical definition of a doubly-linked list node, written as a template holding information of type TYPE:
Each Dnode has both a prev and next pointer. With the prev pointer, it's easy to write the InsertBefore( ) function. Also the RmvNext( ) function can be replaced with a Rmv( ) function that directly removes a node--without having to find the node that precedes it.
The steps for inserting a node into a doubly-linked list are given in Figure 8.4; the steps for removing a node are shown in Figure 8.5. Note that the only difference between InsertBefore( ) and InsertAfter( ) is the interchanging of prev and next.
This next example creates the list shown previously in Figure 8.1(b)--this time using both the InsertBefore( ) and InsertAfter( ) functions. Again, a null-terminated list is built (in both directions) due to the constructor setting the prev and next pointers to null. We've created a dummy header node as we did before:
Sample code for implementing a doubly-linked list is given on disk in the file ch8_2.cpp.
The lists constructed in the previous sections are homogenous. That is, their nodes hold only one kind of data. In contrast, the nodes in a heterogenous list have different kinds of data. As is true with heterogenous arrays, two issues are involved with heterogenous lists: we have to deal with different sized data and typecasting problems.
With linked lists, handling different sized data is easy, since the nodes don't have to be the same size (as do array elements). This fact is due to the non-contiguous nature of linked lists. A heterogenous list node can store its data directly instead of using an indirect pointer scheme. In a sense, the prev and next pointers of a list node can serve the same purpose as the indirect pointers of a heterogenous array: allowing data of different types and sizes.
To avoid clumsiness, however, the prev and next pointers of the different nodes must be type compatible. How can this be accomplished? The following observation will give you a clue: if you look at the insert and remove functions of the Snode and Dnode classes, you'll notice that they do not involve the node data! This fact suggests you can define base classes that deal only with the list aspects of a node, without regard to what is stored on the list. Then, classes could be derived that deal with the different types of node data. The prev and next pointers, typed as base class pointers, can point to any node derived from the base class. Thus, lists with different types of nodes can be handled.
Here is an abstract class, Snodeb, designed for singly-linked list nodes, that uses the concepts of the previous section:
The functions of Snodeb are just like those of Snode, except the links are typed as Snodeb pointers. Also, keep in mind that a Dnodeb class can be similarly defined for doubly-linked nodes.
To show how to create a heterogenous list using Snodeb, we'll use the Shape and Circle class hierarchy defined in Chapter 5 (where heterogenous arrays were discussed). Given those two classes, we can derive node classes specifically for storing Shape and Circle objects:
The following example creates and uses a list with two nodes (plus a dummy header) that stores a shape and circle object:
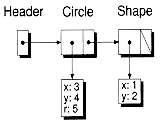
Figure 8.6 illustrates the list that is created. Note in particular that the header, typed as an Snodeb node, doesn't contain any data. We've conveniently eliminated the problem of wasting space in the header for data that isn't used. You'll see this technique used again later in this chapter.
While it's easy to create a heterogenous list, it's another matter to actually use the list. Take a look at what happens if we walk the list created in the previous section and print the areas of the shapes in each node:
A nasty typecasting problem surfaces. We must remember what the node types really are so that the proper Area( ) function is called. This is the same typecasting problem that occurs with all heterogenous containers.
One way to tame the typecasting is to use the same technique we did for arrays: store pointers to the data in the nodes, rather than storing the data directly. Again, it's especially beneficial to use base class pointers. For example, we could define the ShapeNode class as follows, which will work for both Shapes and Circle objects:
Now we can create a heterogenous list, as follows:
The list created is shown in Figure 8.7. Now take a look at what happens when we walk the list:
Because p is defined as an Snodeb pointer, we haven't eliminated the typecasting, but we've at least eliminated the problem of knowing whether a node points to a Shape or Circle object. That is handled by the fact that Area( ) is a virtual function.
We can reduce the typecasting further by providing another function, Next( ), whose sole purpose is to typecast the next pointer as a pointer to a ShapeNode object:
We still must do a typecast for the header node, but at least when walking the list no other typecasts are necessary--as long as we use Next( ) instead of next. We could eliminate the typecast on the header node by defining it as a ShapeNode, rather than an Snodeb object. However, the info field of the header would then be wasted.
We can also create polymorphic list nodes using a method that allows us to store data directly in the nodes. The idea is to define the types of data to be stored on lists as bona fide nodes themselves. We can do this in two basic ways:
1. Derive the data types to be stored on lists from abstract node classes. For example, we could derive Shape from Snodeb:
2. Define the data type to directly have list pointers. For example, you could define Shape to have a next pointer and the corresponding InsertAfter( ) and RmvNext( ) functions:
With both of these techniques, every class derived from Shape (such as Circle) will inherit list pointers and thus will be list nodes themselves. This is better than using indirect data pointers. The resulting list structures will be less complicated and take up less room. However, both techniques require list pointers for all data types to be stored on lists, which may be undesirable. For example, you may want to use the data types for applications other than lists.
Here is an example of the first technique. Note that, instead of writing p->info->Area( ), we write p->Area( ). That is, the info field no longer exists. The node data is a direct part of the node itself:
Contrast this with the second technique:
The second technique is cleaner because we don't need a Next( ) function. The next pointer is already typed as a Shape pointer. Unfortunately, as the code shows, header nodes must store shape data that isn't used. If we make the header an Snodeb node, then typecasting difficulties are created.
The second technique also forces every type of list (such as a shape list, a window list, a bank account list, and so on) to be from a different hierarchy. There is no common Snodeb class. As a result, functions like InsertAfter( ) and RmvNext( ) have to be duplicated for each type of list. Even with these problems, the second technique is often used because of its directness. In fact, you'll see us use it in Chapter 13 when we develop a caching data structure that implements a doubly-linked list of "buckets."
Classes like Snodeb and Snode define the nuts and bolts of a linked list, but they don't allow us to treat linked lists at a high level. For example, it would be convenient to use linked lists the way we use arrays (without the subscripting, of course). Toward this end, it would be helpful to have functions to support such operations as copying, assignment, and concatenation. In this section, we'll show you how to define linked lists as concrete data types. Ten classes are implemented--Snodeb, Slistb, Snode, Slist, TempSlist, Dnodeb, Dlistb, Dnode, Dlist, and TempDlist--to provide all the necessary tools for implementing singly-linked and doubly-linked lists. (Don't worry, many of these classes are nothing but typecasting interfaces--with many functions that can be inlined.)
Before we explain the design details, we should note that, traditionally, many programmers never use linked-lists as separate entities and are prone to directly embedding list pointers (and associated functions) into their objects. It's not clear whether this is due to the historical lack of good development tools (for example, defining and using generic lists in C is somewhat clumsy) or whether the directness outweighs the advantages of reusable linked-list code. It is possible to define reasonably reusable, safe, and efficient linked-list classes using C++, as you are about to see. Only time will tell whether using linked lists as objects in their own right becomes a widespread technique.
Singly-Linked List Abstract Classes
The linked lists that we'll present have the following design features:
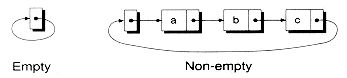
We'll now explain the second feature (circular lists) in detail. Rather than terminate a list by giving the last node a null next pointer, you can instead have the last node point to the first node. Such a list is called a circular list. Figure 8.8 shows an example of a singly-linked circular list with a header node. The figure also shows an empty circular list consisting of a header node that points to itself. With circular lists, node insertion and removal can be done more elegantly. You never have to worry about a prev or next pointer being null, eliminating many special cases, as you'll see later.
We'll now focus on the two classes Snodeb and Slistb, which support singly-linked lists in an abstract sense. (The node data isn't part of their definitions.) The Snodeb class is almost identical to the one given earlier, except that it uses encapsulation to the fullest (all members are protected). It is also set up to support circular lists, through the addition of a SelfRef( ) function:
Because we'll use circular lists, the functions InsertAfter( ) and RmvNext( ) can be coded quite elegantly--with no special cases needed when the list is empty (or about to become empty).
You might try these functions on paper--using various situations that involve circular lists--to convince yourself that they will always work properly (as long as you don't try to remove a list header node).
Complete code for the Snodeb class, as well as the Slistb class (presented next), is given on disk in the files slistb.h and slistb.cpp.
With the Snodeb class available, we can define the Slistb class:
This class is truly abstract, having the pure virtual functions DupNode( ) and FreeNode( ). These are made virtual to support different types of memory allocation. Also, because Slistb doesn't know the type of data to be stored in the nodes, it can't be responsible for constructing them. Note that the code for Slistb will be shared for many types of singly-linked lists.
One of the most unusual features of Slistb is that it is derived from Snodeb. An Slistb object represents the header of a list. Since the list is circular, the last node will point to this header. By making Slistb type-compatible with Snodeb, we alleviate some typecasting difficulties otherwise encountered.
Since Slistb is derived from Snodeb, it inherits a next pointer, which is used to point to the first node of the list or back to itself if the list is empty. Another pointer, back, is defined to point to the last node in the list. This allows the efficient addition of nodes at the end of the list. (Otherwise, you would have to scan the list from start to end.) Interestingly, the presence of the back pointer doesn't mean you can efficiently remove nodes from the end of the list. There's no efficient way to do this with singly-linked lists.
Many design alternatives are possible for circular lists. Figure 8.9 shows some of these alternatives. You can choose whether to have a header, and whether to include the header in the cycle--with or without a back pointer. Figure 8.9(d) shows the alternative we've chosen for the Slistb class. By making the header node part of the cycle, it can serve as a flag to test when the end of the list is reached during a list walk. The IsHeader( ) function is provided for this purpose:
This example uses IsHeader( ) to walk a list:
When deriving the Slistb class, Snodeb was declared as a private base class. This disallows direct access to the next pointer and to the functions InsertAfter( ) and RmvNext( ). Instead, we must use access functions, such as the following Front( ) function:
The Slistb class defines its own InsertAfter( ) and RmvNext( ) functions, which is done to support the back pointer. Whenever a node is added to the end of the list, or if the last node of the list is removed, the back pointer must be updated. The RmvNext( ) function includes a test to ensure that we don't try to remove the list header itself. Both functions assume that the appropriate node actually resides on the list.
Three more higher-level functions that use InsertAfter( ) and RmvNext( ) are provided to allow convenient insertion to the front or back of the list, and to remove the front of the list:
A default constructor is provided to create an empty list:
The constructor calls the MakeEmpty( ) function, which makes the list point to itself and also sets the back pointer to point to the list header:
A companion function can be used to test if a list is empty:
You can clear a list by calling the Clear( ) function:
The Clear( ) function works by freeing each node in the list and then setting the list empty. Note that FreeNode( ) is a pure virtual function. Since Slistb doesn't know what kind of data is stored in a node, it can't properly free the node. Classes derived from Slistb (such as Slist, to be presented later in this chaper) are responsible for providing the appropriate definition of FreeNode( ).
The Slistb class has a virtual destructor. Contrary to what you might think, this destructor doesn't do anything, not even call Clear( ) to empty the list! The reason is that Clear( ) calls FreeNode( ) and, since that function is virtual, it isn't safe to call it from the base class destructor. Classes derived from Slistb should override their destructors to call Clear( ).
Two functions are provided to help in concatenating one list to the end of another, and in doing list copying. There's only one difference between list concatenation and copying. When a copy is made, the target list is cleared first:
Note that Concatenate( ) calls the virtual function DupNode( ), which is supposed to allocate a new node and duplicate the data from the source node into it. Again, derived classes must provide their own versions of DupNode( ) to handle the type of data they are going to use.
An Absorb( ) function is provided, similar to Concatenate( ), which can be used to "smash" two lists together. The nodes of the list to be appended are not copied, but rather are absorbed through pointer manipulation. The source list then becomes empty. The steps in the absorption process are illustrated in Figure 8.10.
The counterpart to Absorb( ) is the SplitAfter( ) function, which splits a source list after some specified node n. The tail of the split list is absorbed onto the end of a target list. If the target list comes in empty, the effect is to split the source list into two parts. The steps involved are similar to Absorb( ) in that most of the work concentrates on adjusting the back pointers. Figure 8.11 shows the result of splitting a list after the first node.
Now that we've defined the Snodeb and Slistb base classes, we can derive specific classes tailored to nodes of a given type. To provide generality, the Snode and Slist classes are defined as templates. We start with the Snode class:
This class allows data of type TYPE to be stored on a node. Of particular importance is the Next( ) function, which typecasts the next pointer to be of the proper type, for reasons we gave earlier.
The Slist class, used to create lists storing TYPE data, is defined as follows:
Complete code for the Snode and Slist classes is given on disk in the files slist.h and slist.mth. A test program is given in the file sltst.cpp.
The main purpose of Slist is to serve as a type-specific interface to the Slistb class. Many of the functions of Slist are nothing more than typecasting interfaces that can be easily inlined, such as the following Front( ) and Back( ) functions:
The typecasts in these functions are somewhat unsafe. In the case of an empty list, both Front( ) and Back( ) will return a pointer to the header node, which isn't an Snode<TYPE> node even though it's returned as one. Before you try to redesign this, remember that the design we've given is really no more unsafe than returning a null pointer in case of an empty list. In either case, you must check for a valid pointer. The IsHeader( ) function can be used for that purpose (not shown here). The Header( ) function, which returns a pointer to the header node, is the counterpart to IsHeader( ). The Header( ) function has a similar problem to Front( ) and Back( ) in that it returns a pointer to the header node as though it were an Snode<TYPE> node:
The Header( ) function was designed for typecasting convenience when iterating through a list, and should be used only for that purpose. The followingNodeBeforeMatch( ) function shows an example of using Header( ):
Given some data of type TYPE, this function scans the list looking for the node that contains matching data. Note that the node before the matching node is returned, in case you want to remove the matching node using RmvNext( ). BothHeader( ) and Next( ) return Snode<TYPE> pointers, which alleviate the need to use direct typecasts between Snodeb pointers and Snode<TYPE> pointers. The typecasting problem isn't eliminated; it's just encapsulated as much as possible.
The following InsertAfter( ) and RmvNext( ) functions also serve as type-casting interfaces:
Other functions are defined similarly, such as AttachToFront( ), RmvFront( ), and AttachToBack( ). As is true with the Slistb class, these functions are only responsible for attaching or detaching nodes to a list; they don't allocate or deallocate the nodes. Since Slist knows the type of node data to be used, functions can be added to automatically allocate and de-allocate the nodes, such as the following AddAfter( ) and DelNext( ) functions:
The AllocNode( ) and FreeNode( ) functions are virtual. Here are the specific versions for the Slist class:
The typecast used in FreeNode( ) seems rather unsafe, since it assumes that n is actually an Snode<TYPE> node. Consequently, you'll notice this function(as well as AllocNode( )) is protected. Note that n is guaranteed to be an Snode<TYPE> node for all uses of FreeNode( ) in the Slist class.
You may wonder why the unsafe typecast is used at all. Why not instead make the destructor for Snodeb virtual? Then, the delete operator would work properly without the typecast. However, adding a virtual function to Snodeb would add overhead in the form of one extra pointer (to the virtual function table) in every node. The typecast, then, can save a lot of space in the lists. Here, we're trading elegance for space efficiency. As always, you should pay attention to details like this, particularly if your designs are to become part of a general-purpose library.
The following DupNode( ) function, used to create a copy (except for the next pointer) of a node, is related to AllocNode( ):
Recall that SListb::Copy( ) uses DupNode( ) when making copies of each node in a list. The Slistb::Copy( ) function is used by Slist::Copy( ), which in turn is used by the operator=( )function:
In addition to overloading the '=' operator, we've overloaded the '+=' operator to provide a convenient notation for concatenating both single nodes and lists onto other lists:
The Slist class provides another way to add one list to another by using the '+' operator:
The operator+( ) function makes a copy of both source operands and returns the result as a new list. This allows statements like the following to be used, where a, b, and c are lists:
You might think a lot of copying is taking place in such statements: one copy made in returning the result and another in assigning the result to the destination list. Instead, a clever trick is used to avoid the copying. The temporary list that's constructed to hold the result can be absorbed (using Absorb( )) into the list that's returned. The returned list can then be absorbed into the destination list, which is cleared beforehand. (Recall the Absorb( ) function smashes two lists together, rather than copying the nodes.)
In effect, we must find a way for the copy constructor (used in the function return) and the overloaded assignment operator (used in the assignment) to use absorption rather than copying. How can we do this? One way is to provide special versions of the copy constructor and assignment operator that work only for temporary lists. You'll notice that operator+( ) returns a TempSlist object, instead of an Slist object. The TempSlist class is defined as follows:
Complete code for the TempSlist class is given on disk in the file Slist.h.
The sole purpose of TempList is to provide a way to trap cases when the list is meant to be temporary. A TempSlist object is just like an Slist object: all that's changed is the type name (and the implicit restriction of its use only for temporary lists). The class has a singlecopy constructor that takes a normal list and uses absorption to turn it into a temporary list:
The TempSlist copy constructor is used in returning the result of a list addition. Then, if the temporary list is to be used in an assignment (such as c = a + b), the following overloaded assignment operator for Slist objects is used:
You should walk through the steps involved in statements like c = a + b to assure yourself that indeed no redundant copying takes place. The trick of defining a new type, such as TempSlist, for the sole purpose of trapping special cases in overloaded function calls is useful to remember.
There's one last function to consider for Slist--the destructor:
This destructor causes any remaining nodes in the list to be freed at list-destruction time. As we mentioned earlier, it's very important that the call to Clear( ) be placed here, not in the base Slistb class destructor, due to the virtual function calls to FreeNode( ) inside Clear( ).
In the following example, we've used the Slist class to construct and manipulate singly-linked lists:
The five classes that support doubly-linked lists--Dnodeb, Dlistb, Dnode, Dlist, and TempDlist--are very similar to their singly-linked counterparts and will not be shown here. (They are given on disk, however.) Figure 8.12 shows examples of circular doubly-linked lists that can be created using the five classes.
Complete code for the Dnodeb, Dlistb, Dnode, Dlist, and TempDlist classes is given on disk in the files dlistb.h, dlistb.cpp, dlist.h, and dlist.mth. A test program is given in the file dltst.cpp.
With AllocNode( ) and FreeNode( ) available as virtual functions, we can create many variations in allocating the nodes of linked lists. In this section, we'll look at some of the possibilities. We'll culminate with a hybrid array-based linked-list design.
With AllocNode( ) and FreeNode( ) available as virtual functions, we can create many variations in allocating the nodes of linked lists. In this section, we'll look at some of the possibilities. We'll culminate with a hybrid array-based linked-list design.
Cursor-Based Singly-Linked Lists
Cursor-Based Doubly-Linked Lists
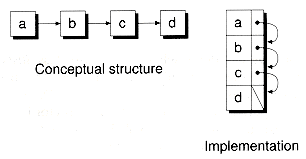
While the Cslist class caches freed nodes, it still uses the heap to allocate nodes initially. Also, each node is allocated separately, which can lead to heap fragmentation. Another alternative is to allocate the nodes in blocks. In fact, if you know the maximum size of a list ahead of time, you can pre-allocate the nodes in a single array. The result is a hybrid structure--an array-based linked list. Figure 8.14 shows an example of a null-terminated singly-linked list where all the nodes are allocated contiguously in an array.
It's actually quite easy to derive array-based linked lists from the Slist and Dlist classes and, in the process, reuse a lot of existing code. The secret is to include a constructor that allocates an array of nodes, and then to override AllocNode( ) to grab nodes from this array. Also, a free list can be maintained simultaneously with the main list, threading together all the nodes in the array that are not in use. Unlike the Cslists used in the previous section, though, each array-based list will have its own free list, rather than sharing a global one. The ArraySlist class, sketched below, illustrates how an array-based singly-linked list can be defined:
Complete code for the ArraySlist class is given on disk in the files aslist.h and aslist.mth. A test program is provided in the file asltst.cpp. Also, a doubly-linked version, ArrayDlist, is provided in the files adlist.h, adlist.mth, and adltst.cpp.
The ArraySlist constructor sets up the array-based linked list by calling a Setup( ) function, which allocates an array of nodes of size mn.
The node array that gets created is actually a variable-length array, where num_nodes represents the logical length and max_nodes represents the dimensioned length. Initially, no nodes are in use. Note that the array's logical length can only grow, not shrink. When a node is to be freed, it is placed on the free list. Eventually, all the nodes will either be on the main list or the free list. As we did for the variable-length arrays defined in Chapter 4, the node array is actually constructed as an array of characters. This prevents the nodes from being constructed until they are actually used.
When a node is to be used, the placement new operator is called to handle the construction of the nodes. This can be seen in the following AllocNode( ) function (which overrides Slist's version):
The AllocNode( ) function works as follows: if the free list is empty (which it will be at the start), then a node is grabbed from the array and constructed in place. It's possible for all the nodes in the array to be in use, in which case the list is full, so a null pointer is returned. If the free list isn't empty, one of its nodes is used. It's important to realize that the nodes themselves are never moved physically. All that changes is their placement either on the main list or the free list.
The FreeNode( ) function works by attaching a node onto the free list. A critical part of this process is the call to the node's destructor--using an explicit destructor call. This must be done because AllocNode( ) assumes that the nodes it grabs aren't constructed.
We explicitly destroy the node to ensure that the destructor for the info field is called. Note, however, that the next pointer will be set to point to the next node in the free list. Thus, nodes in the free list are actually partially constructed. Figure 8.15 shows a sample list created with the ArraySlist class, with some nodes on the main list (fully constructed), some on the free list (partially constructed), and some nodes not yet constructed. Note that the main list and free list headers are stored separately from the node array.
Even though a node might be destroyed, it isn't actually freed until the list itself is destroyed, as the following ArraySlist destructor shows.
The ArraySlist destructor is somewhat tricky because the destructors for the nodes must be handled properly. It's quite possible for some of the nodes to be in use (and thus constructed) but others to be unused (and thus be unconstructed). Somehow, the ArraySlist destructor must cause the node destructor to be called only for those nodes currently in use. This is accomplished by calling the following virtual Clear( ) function:
Once the nodes in use are destroyed, the memory for the nodes is de-allocated by calling delete in the ArraySlist destructor. The nodes are de-allocated as though they were an array of characters, which is how they were allocated initially. The typecast to char * is important; otherwise, the node destructors would be erroneously called again.
Array-based linked lists provide compactness and speed. Because they are contiguous, array-based linked lists don't waste space that might result from heap fragmentation. Also, adding and removing nodes from the list is very fast since no heap manipulation is used. Of course, these improvements come at a price: you must allocate the maximum size of the linked list ahead of time, negating one of the advantages of linked lists. However, all other advantages remain, the most important being the ability to rearrange the elements of the list with minimal data movement.
If you wish to use array-based linked lists, you should be aware that yet another variation is possible. Rather than use pointers for the node links, you can use array indexes. For example, a singly-linked node might be defined as follows:
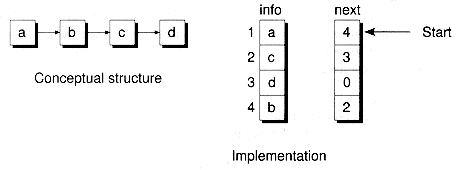
The next variable is now an index that provides the offset in the array to the next node in the list. This index is sometimes called a cursor. In fact, array-based linked lists that use indexes rather than pointers are often called cursor-based linked lists. Figure 8.16 shows an example of a null-terminated, cursor-based singly-linked list. In the figure, it's assumed that the elements are indexed starting at 1, and that 0 represents the end of the list.
You gain the following advantages by using cursors instead of pointers for links:
There is one drawback, however, to the use of cursors rather than pointers: cursors are slower. To find the next node using a cursor, subscript arithmetic must be used (involving an addition and multiplication). In contrast, to find the next node using a pointer, a simple pointer de-reference is all that's required.
There's another variation sometimes used with cursors. Represent the linked list as two separate parallel arrays--one holding the node data and one holding the cursors--rather than implementing a single node array that holds both. In Figure 8.17, the singly-linked list portrayed in Figure 8.16 is implemented using parallel arrays.
The following CursorSlist class uses this parallel array approach to implement a singly-linked list as a concrete data type:
Complete code for the CursorSlist class is given on disk in the files curslist.h and curslist.mth. A test program is given in the file cursltst.cpp.
The first element of the next array is reserved for the list header, and the list is circular. Thus, an empty list has next[0] = 0. Note that the reserved header element forces all non-header list elements to have cursors > 0. To avoid wasting node data for the header, the info array has one less element than next. Given a positive cursor p, the elements info[p-1] and next[p] make up, conceptually, one full list node.
In addition to the two arrays, we need to provide some other variables. The back variable is a cursor to the last node on the list. If the list is empty, back = 0. The num_node variable keeps track of the dimensioned size of the arrays. As is the case with the ArraySlist class, CursorSlist incorporates a built-in free list. The avail cursor points to the front of the free list. Initially, all nodes except for the header are placed on the free list. (In contrast, the ArraySlist class started the free list as an empty list). Thus, avail is initialized to one. Note that the free list does not use a next element for its header and is null-terminated, with the cursor of the last node being zero. (Recall that zero can't index a non-header node.)
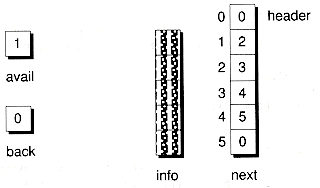
The following Alloc( ) and MakeEmpty( ) functions, called by the constructor, show how a CursorSlist object is set up to represent an empty list. Figure 8.18 illustrates the resulting layout.
The Alloc( ) function allocates the info array as unconstructed bits. The corresponding info element will be constructed (using an in-place construction process) only when a node is placed on the main list. The following InsertAfter( ) and AddAfter( ) functions show how nodes are obtained from the free list and added to the main list.
It's interesting to compare node insertions using cursors with those using pointers, as shown in Table 8.2.
Removing a node from a list works in the opposite fashion. The node is detached from the list and placed at the front of the free list. The node data is then explicitly destructed. The following RmvNext( ) and DelNext( ) functions show the details:
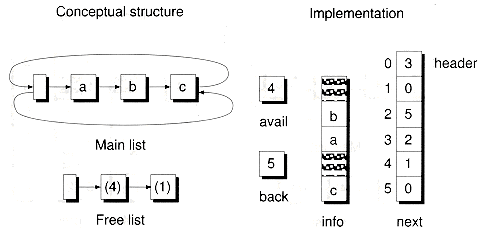
Figure 8.19 illustrates the layout of a cursor-based list with nodes both on the main list and free list.
The CursorSlist class has functions similar to the ArraySlist class, such as Front( ), Back( ), IsHeader( ), AddToFront( ), AddToBack( ), and so on. One unusual function is the following overloaded [ ] operator function (a const version is also supplied in the class):
This allows you to obtain the information stored at a node by using a normal array-subscripting operation. The index p must point to a valid non-header node, but that isn't checked. (Doing so would be very difficult.) Here's an example, of walking through a list and printing out the node information:
The last statement calls the Next( ) function, which allows you to conveniently get the next node in sequence:
A doubly-linked cursor-based list can be defined by adding a third array, representing prev cursors, as illustrated in Figure 8.20. Note that the free list is implemented as a singly-linked null-terminated list, even though the main list is a circular doubly-linked list. The CursorDlist class, a doubly-linked analog to CursorSlist, can be defined as:
Complete code for the CursorDlist class is given on disk in the files curdlist.h and curdlist.mth. A test program is given in the file curdltst.cpp.
The CursorDlist class is very similar to the other list classes we've defined, so we won't show it in detail here. However, it's interesting to note the symmetry of the InsertAfter( ), InsertBefore( ), and Rmv( ) functions. (The comments illustrate equivalent pointer-based manipulations.)
In this chapter, you've seen some of the variations possible for linked lists. These data structures are quite versatile and, along with arrays, form the basis for many of the more complicated data structures. We've attempted to turn linked lists into concrete data types with classes like Slist, ArraySlist, CursorSlist, and so on. However, keep in mind that list-type links are sometimes directly embedded into other objects, as you will see in later chapters. As such, the most important functions to keep in mind are ones like InsertAfter( ), InsertBefore( ), Rmv( ), and RmvNext( ), which work on a node-by-node basis.
The linked lists presented here are designed to work in memory. However, it's quite possible, and useful, to have linked lists that are stored on files. This can be done by using file offsets for links (equivalent to cursors), rather than pointers. In later chapters, we'll show you how to do this.
One final comment: as is true with any data structure, linked lists are designed for certain types of applications and may work very poorly for others. Linked lists excel in cases where you need only sequential access and where the objects to be stored are rearranged frequently. Linked lists aren't as useful with random access or when the objects being stored need to be searched. Other data structures--such as arrays or search trees--work better in this regard.
template<class TYPE>
void Snode<TYPE>::InsertAfter(Snode<TYPE> *n)
// Insert node n after this node
{n->next = next; // See Fig 8.2a
next = n; // See Fig 8.2b
}
Snode<char> mylist('a');mylist.InsertAfter(new Snode<char>('c'));mylist.InsertAfter(new Snode<char>('b'));Figure 8.2 Inserting a node into a singly-linked list.

Snode<char> *p = &mylist;
while(p && p->next != q) p = p->next; // Scan down the list
if (p) p->InsertAfter(n); // Equivalent to inserting before q
Snode<char> mylist(0); // Header node, with an arbitrary info field
mylist.InsertAfter(new Snode<char>('c')); // List built backwardsmylist.InsertAfter(new Snode<char>('b'));mylist.InsertAfter(new Snode<char>('a'));template<class TYPE>
Snode<TYPE> *Snode<TYPE>::RmvNext()
// Removes the node following this node.
// Tests for next being null.
// Returns a pointer to the node removed.
{Snode *p = next;
if (p) next = p->next; // See Fig 8.3
return p;
}
Figure 8.3 Removing a node from a singly-linked list.
Snode<char> *p;
p = mylist.RmvNext(); // Detach the node from the list
delete p; // Then, de-allocate the node
Snode<char> *p = &mylist; // Point to head of list
while(p && p->next != q) p = p->next;
if (p) p->RmvNext();

Doubly-Linked List Nodes
template<class TYPE>
struct Dnode {TYPE info;
Dnode<TYPE>*prev;
Dnode<TYPE>*next;
Dnode(const TYPE &x);
void InsertBefore(Dnode<TYPE> *n);
void InsertAfter(Dnode<TYPE> *n);
Dnode<TYPE> *Rmv();
} ;
template<class TYPE>
Dnode<TYPE>::Dnode(const TYPE &x)
: info(x)
{prev = 0; next = 0;
}
template<class TYPE>
void Dnode<TYPE>::InsertBefore(Dnode<TYPE> *n)
// Inserts node n before this node.
// Tests for prev being null.
{n->prev = prev;
n->next = this;
if (prev) prev->next = n;
prev = n;
}
template<class TYPE>
void Dnode<TYPE>::InsertAfter(Dnode<TYPE> *n)
// Attaches node n after this node.
// Tests for next being null.
{n - > next = next; // See Fig 8.4a
n - > prev = this; // See Fig 8.4b
if (next) next->prev = n; // See Fig 8.4c
next = n; // See Fig 8.4d
}
template<class TYPE>
Dnode<TYPE> *Dnode<TYPE>::Rmv()
// Removes this node from the list it is on.
// Tests for prev and next being null.
{if (prev) prev->next = next; // See Fig 8.5a
if (next) next->prev = prev; // See Fig 8.5b
return this;
}
Dnode<char> mylist(0); // Header with arbitrary info field
mylist.InsertAfter(new Dnode<char>('c'));Dnode<char> *p = new Dnode<char>('b');mylist.InsertAfter(p);
p->InsertBefore(new Dnode<char>('a'));
Figure 8.4 Inserting a node into a doubly-linked list.

Figure 8.5 Removing a node from a doubly-linked list.
HETEROGENOUS LISTS
Abstract List Nodes
struct Snodeb { // An abstract singly-linked list node base classSnodeb *next; // Pointer to next node in the list
Snodeb();
void InsertAfter(Snodeb *n);
Snodeb *RmvNext();
};
struct ShapeNode : public Snodeb {Shape info;
ShapeNode(float x=0, float y=0);
};
ShapeNode::ShapeNode(float x, float y)
: info(x, y)
{// Nothing else to do
}
struct CircleNode : public Snodeb {Circle info;
CircleNode(float x = 0, float y = 0, float r = 0);
};
CircleNode::CircleNode(float x, float y, float r)
: info(x, y, r)
{// Nothing else to do
}
Snodeb mylist; // Create the header
mylist.InsertAfter(new ShapeNode(1, 2));
mylist.InsertAfter(new CircleNode(3, 4, 5));
Figure 8.6 A heterogenous list.

Polymorphic List Nodes
Snodeb *p = &mylist.next;
cout << "Area is: " << ((CircleNode *)p)->info.Area() << '\n';
p = p->next;
cout << "Area is: " << ((ShapeNode *)p)->info.Area() << '\n';
struct ShapeNode : public Snodeb {Shape *info; // Point to shape object
ShapeNode(const Shape *p);
};
ShapeNode::Shape(const Shape *p)
{info = p;
}
Snodeb mylist; // Create the header.
mylist.InsertAfter(new ShapeNode(new Shape(1, 2)));
mylist.InsertAfter(new ShapeNode(new Circle(3, 4, 5)));
Snodeb *p = &mylist.next;
cout << "Area is: " << ((ShapeNode *)p)->info->Area() << '\n';
p = p->next;
cout << "Area is: " << ((ShapeNode *)p)->info->Area() << '\n';
ShapeNode *ShapeNode::Next()
{return (ShapeNode *)next;
}
. . .
ShapeNode *p = ((ShapeNode *)(&mylist))->Next();
cout << "Area is: " << p->info->Area() << '\n';
p = p->Next( );
cout << "Area is: " << p->info->Area() << '\n';
Figure 8.7 A heterogenous list using indirect pointers.
List Nodes as Roots of Class Hierarchies
class Shape : public Snodeb {// . . . Shape class as in Chapter 5
Shape *Next();
};
. . .
Shape *Shape::Next()
{return (Shape *)next;
}
class Shape {// . . . Shape class code as in Chapter 5
Shape *next;
void InsertAfter(Shape *n);
Shape *RmvNext();
};
Snodeb mylist; // Create the header
mylist.InsertAfter(new Shape(1, 2)));
mylist.InsertAfter(new Circle(3, 4, 5)));
Shape *p = ((Shape *)(&mylist))->Next();
cout << "Area is: " << p->Area() << '\n';
p = p->Next();
cout << "Area is: " << p->Area( ) << '\n';
Shape mylist; // Create a header with shape data not used
mylist.lnsertAfter(new Shape(1, 2)));
mylist.InsertAfter(new Circle(3, 4, 5)));
Shape *p = mylist.next;
cout << "Area is: " << p->Area() << '\n';
p = p->next;
cout << "Area is: " << p->Area() << '\n';
LINKED LISTS AS CONCRETE DATA TYPES
Linked List Design Features
 Header nodes are used to allow convenient insertion into the front of a list. Also, extra back pointers are added to allow convenient insertions to the back of lists.
Header nodes are used to allow convenient insertion into the front of a list. Also, extra back pointers are added to allow convenient insertions to the back of lists. Circular lists are used rather than null-terminated lists (you'll see this arrangement shortly) because they lead to more elegant insertion and removal operations.
Circular lists are used rather than null-terminated lists (you'll see this arrangement shortly) because they lead to more elegant insertion and removal operations. The linked list code is abstracted so that it can be reused for lists storing different types of data.
The linked list code is abstracted so that it can be reused for lists storing different types of data. The list classes are designed with robustness and efficiency in mind--with a full complement of constructors, destructors, and overloaded operators.
The list classes are designed with robustness and efficiency in mind--with a full complement of constructors, destructors, and overloaded operators. The lists are homogenous by nature, although heterogenous lists can be created by using pointers as the node data types.
The lists are homogenous by nature, although heterogenous lists can be created by using pointers as the node data types. The allocation of nodes for a linked list is made flexible so that many different memory allocation schemes can be supported.
The allocation of nodes for a linked list is made flexible so that many different memory allocation schemes can be supported. We implement a clever way to efficiently return linked lists by value. This technique, in combination with overloading the '+' operator, allows us to use expressions like a = b + c without redundant copying.
We implement a clever way to efficiently return linked lists by value. This technique, in combination with overloading the '+' operator, allows us to use expressions like a = b + c without redundant copying.Figure 8.8 A circular singly-linked list.
Singly-Linked List Abstract Classes
class Snodeb {protected:
Snodeb *next;
void InsertAfter(Snodeb *n);
Snodeb *RmvNext();
void SelfRef(); // New function
friend class Slistb; // For convenient access
};
void Snodeb::SelfRef()
// Make this node point to itself
{next = this;
}
void Snodeb::InsertAfter(Snodeb *n)
{n->next = next;
next = n;
}
Snodeb *Snodeb::RmvNext()
{Snodeb *p = next;
next = p->next;
return p;
}

class Slistb : private Snodeb {protected:
virtual void MakeEmpty();
public:
Snodeb *back;
Slistb();
virtual ~Slistb();
Snodeb *Front() const;
Snodeb *Back() const;
virtual Snodeb *DupNode(const Snodeb *n) = 0;
virtual void FreeNode(Snodeb *n) = 0;
virtual void Clear();
int Copy(const Slistb &sl);
int Concatenate(const Slistb &sl);
void InsertAfter(Snodeb *a, Snodeb *b);
Snodeb *RmvNext(Snodeb *n);
Snodeb *RmvFront();
void AttachToFront(Snodeb *n);
void AttachToBack(Snodeb *n);
void Absorb(Slistb &sl);
void SplitAfter(Snodeb *n, Slistb &sl);
int IsEmpty() const;
int IsHeader(const Snodeb *n) const;
};
int Slistb::IsHeader(const Snodeb *n) const
// Sees if node n is the list head
{return n == this;
}
Snodeb *p = &mylist;
while(1) {p = p->next;
if (mylist.IsHeader(p)) break;
// Process node p
}
Figure 8.9 Some alternative circular list designs.

(a) No header
(b) Header not in cycle

(c) Header in cycle

(d) Header in cycle w/back pointer
Snodeb *Slistb::Front() const
{return next; // Header is returned if list is empty
}
void Slistb::InsertAfter(Snodeb *a, Snodeb *b)
{a->InsertAfter(b);
if (a == back) back = b; // Assumes a resides on this list
}
Snodeb *Slistb::RmvNext(Snodeb *n)
// ASSUMES n resides on this list.
{if (n->next == this) return 0; // Can't detach list header!
Snodeb *p = n->RmvNext();
if (p == back) back = n;
return p;
}
void Slistb::AttachToFront(Snodeb *n)
// Inserts node n after the header
{InsertAfter(this, n);
}
Snodeb *Slistb::RmvFront()
// Removes the first node from the list. Note that
// RmvNext() will return 0 if the list is empty.
{return RmvNext(this);
}
void Slistb::AttachToBack(Snodeb *n)
// Inserts the node n after the back node.
{InsertAfter(back, n);
}
Slistb::Slistb()
{MakeEmpty();
}
void Slistb::MakeEmpty()
{SelfRef();
back = this;
}
int Slistb::IsEmpty() const
{// Typecast needed because of const keyword
return next == (Snodeb *)this;
}
void Slistb::Clear( )
{Snodeb *n = next;
while(!IsHeader(n)) {Snodeb *nn = n->next;
FreeNode(n);
n = nn;
}
MakeEmpty();
}
int Slistb::Concatenate(const Slistb &sl)
{if (this == &sl) return 0; // Can't concatenate to self
const Snodeb *p = sl.next;
while(!sl.IsHeader(p)) { // For all nodes in slSnodeb *q = DupNode(p); // Make duplicate of the node
if (q == 0) return 0; // Incomplete copy made
AttachToBack(q);
p = p->next;
}
return 1; // Successful concatenation
}
int Slistb::Copy(const Slistb &sl)
{if (this == &sl) return 1; // Nothing to do
Clear();
return Concatenate(sl);
}
void Slistb::Absorb(Slistb &sl)
{if (sl.IsEmpty() | | this == &sl) return; // Already absorbed
back->next = sl.next; // See Figure 8.10a
sl.back->next = this; // See Figure 8.10b
back = sl.back; // See Figure 8.10c
sl.MakeEmpty(); // See Figure 8.10d
}
Figure 8.10 Absorbing one list into another.
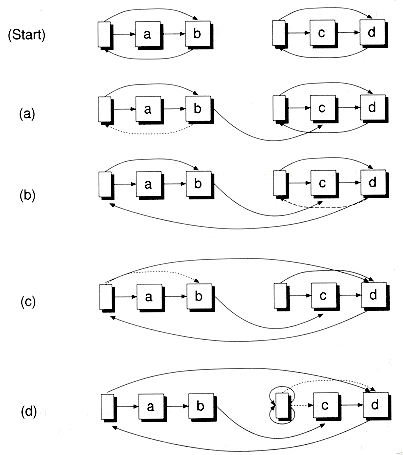
Figure 8.11 Splitting a list.

void Slistb::SplitAfter(Snodeb *n, Slistb &tl)
// Assumes n is actually on this list. It's allowed to be
// the header (in which case, the list will go empty).
{if (this == &tl) return; // Can't split to yourself
if (n == back) return; // Nothing to split
tl.back->next = n->next;
tl.back = back;
back->next = &tl;
n->next = this;
back = n;
}
Singly-Linked List Templates
template<class TYPE>
class Snode : public Snodeb {public:
TYPE info;
Snode();
Snode(const TYPE &x);
Snode<TYPE> *Next();
};
template<class TYPE>
Snode<TYPE> *Snode<TYPE>::Next()
// This function is for typecasting convenience
{return (Snode<TYPE> *)next;
}
template<class TYPE>
class Slist : private Slistb {protected:
virtual Snode<TYPE> *AllocNode(const TYPE &x);
virtual Snodeb *DupNode(const Snodeb *sn);
virtual void FreeNode(Snodeb *dn);
Slistb::MakeEmpty; // Keep this protected
public:
friend class TempSlist<TYPE>;
friend class ArraySlist<TYPE>;
Slist();
Slist(const Slist<TYPE> &s);
Slist(TempSlist<TYPE> &s);
virtual ~Slist();
void operator=(const Slist<TYPE> &s);
void operator=(TempSlist<TYPE> &s);
Snode<TYPE> *Header() const;
Snode<TYPE> *Front() const;
Snode<TYPE> *Back() const;
Slistb::Clear; // Make this base function public
Slistb::IsEmpty; // Make this base function public
int Copy(const Slist<TYPE> &sl);
void InsertAfter(Snode<TYPE> *a, Snode<TYPE> *b);
void AttachToFront(Snode<TYPE> *n);
void AttachToBack(Snode<TYPE> *n);
Snode<TYPE> *RmvNext(Snode<TYPE> *n);
Snode<TYPE> *RmvFront();
int DelNext(Snode<TYPE> *n);
int DelFront();
void Absorb(Slist<TYPE> &sl);
void SplitAfter(Snode<TYPE> *n, Slist<TYPE> &sl);
int IsHeader(const Snode<TYPE> *n) const;
int Concatenate(const Slist<TYPE> &sl);
int operator+=(const Slist<TYPE> &sl);
Snode<TYPE> *operator+=(const TYPE &x);
friend TempSlist<TYPE>
operator+(const Slist<TYPE> &a, const Slist<TYPE> &b);
Snode<TYPE> *
NodeBeforeMatch(const TYPE &x, Snode<TYPE> *p=0) const;
Snode<TYPE> *AddToFront(const TYPE &x);
Snode<TYPE> *AddToBack(const TYPE &x);
Snode<TYPE> *AddAfter(const TYPE &x, Snode<TYPE> *n);
};

template<class TYPE>
Snode<TYPE> *Slist<TYPE>::Front() const
{return (Snode<TYPE> *)Slistb::Front();
}
template<class TYPE>
Snode<TYPE> *Slist<TYPE>::Back() const
{return (Snode<TYPE> *)Slistb::Back( );
}
template<class TYPE>
Snode<TYPE> *Slist<TYPE>::Header() const
{return (Snode<TYPE> *)this;
}
template<class TYPE>
Snode<TYPE> *Slist<TYPE>::
NodeBeforeMatch(const TYPE &x, Snode<TYPE> *p) const
{// Note that Next() is used, rather than 'next'
// directly. This is for typecasting convenience.
if (p == 0) p = Header(); // p == 0 is the default
while(!IsHeader(p->Next())) { // Scan until end of listif (p->Next()->info == x) return p; // Match found
p = p->Next();
}
return 0; // No match
}
template<class TYPE>
void Slist<TYPE>::InsertAfter(Snode<TYPE> *a, Snode<TYPE> *b)
{Slistb::InsertAfter(a, b);
}
template<class TYPE>
Snode<TYPE> *Slist<TYPE>::RmvNext(Snode<TYPE> *n)
{return (Snode<TYPE> *)(Slistb::RmvNext(n));
}
template<class TYPE>
Snode<TYPE> *Slist<TYPE>::AddAfter(const TYPE &x, Snode<TYPE> *n)
{Snode<TYPE> *p = AllocNode(x);
if (p) InsertAfter(n, p);
return p;
}
template<class TYPE>
int Slist<TYPE>::DelNext(Snode<TYPE> *n)
{Snode<TYPE> *p = RmvNext(n);
if (p) {FreeNode(p);
return 1;
}
return 0;
}
template<class TYPE>
Snode<TYPE> *Slist<TYPE>::AllocNode(const TYPE &x)
// A function that allocates a new Snode<TYPE> node,
// holding a copy of x as its data
{return new Snode<TYPE>(x);
}
template<class TYPE>
void Slist<TYPE>::FreeNode(Snodeb *n)
// Deletes node n. Assumed to be a Snode<TYPE> node.
{delete((Snode<TYPE> *)n);
}
template<class TYPE>
Snodeb *Slist<TYPE>::DupNode(const Snodeb *n)
{return AllocNode(((Snode<TYPE> *)n)->info);
}
template<class TYPE>
int Slist<TYPE>::Copy(const Slist<TYPE> &sl)
{return Slistb::Copy(sl);
}
template<class TYPE>
void Slist<TYPE>::operator=(const Slist<TYPE> &sl)
{Copy(sl); // Traps copies to self
}
template<class TYPE>
int Slist<TYPE>::operator+=(const Slist<TYPE> &sl)
{return Concatenate(sl);
}
template<class TYPE>
Snode<TYPE> *Slist<TYPE>::operator+=(const TYPE &x)
{return AddToBack(x);
}
template<class TYPE>
TempSlist<TYPE> operator+(const Slist<TYPE> &a, const Slist<TYPE> &b)
{Slist<TYPE>copy_of_a(a);
copy_of_a.Concatenate(b);
return copy_of_a; // copy_of_a absorbed into temp result
}
a = b + c; // Add lists a and b together; store in c
template<class TYPE>
class TempSlist : private Slist {private:
friend class Slistb<TYPE>;
virtual Snodeb *DupNode(const Snodeb *);
virtual void FreeNode(Snodeb *);
public:
TempSlist(Slist<TYPE> &sl);
} ;

template<class TYPE>
TempSlist<TYPE>::TempSlist(Slist<TYPE> &sl)
{Slistb::Absorb(sl); // Note: sl goes empty
}
template<class TYPE>
void Slist<TYPE>::operator=(TempSlist<TYPE> &sl)
{Clear();
Slistb::Absorb(sl; // sl goes empty in the process
}
template<class TYPE>
Slist<TYPE>::~Slist()
{Clear();
}
void f()
{Slist<char> x, y, z; // Construct empty lists
x.AddToBack('a');x += 'b'; // Same as x = AddToBack('b');y += 'c';
y += 'd';
x += y; // x now holds [a b c d], y holds [c d]
y.Clear(); // Remove all nodes from y
y.AddToFront('f');y.AddToFront('e');z = x + y; // z now holds [a b c d e f], x [a b c d], y [e f]
Snode<char. *p = z.NodeBeforeMatch('c); // Look for 'c'if (p) z.RmvNext(p); // Remove node holding 'c'
// All lists destroyed implicitly here
}
Doubly-Linked List Classes

VARIATIONS ON A THEME
VARIATIONS ON A THEME
Array-Based Linked Lists
template<class TYPE>
class ArraySlist : private Slist<TYPE> {protected:
virtual Snode<TYPE> *AllocNode(const TYPE &d);
virtual void FreeNode(Snodeb *n);
int nodes_used, max_nodes;
Slist<TYPE> free_list;
Snode<TYPE> *nodes;
virtual void MakeEmpty();
void Setup(int mn);
. . . // Other private functions
public:
ArraySlist(int mn);
virtual ~ArraySlist();
virtual void Clear();
. . . // Other public functions
};
Figure 8.14 An array-based linked list.

template<class TYPE>
ArraySlist<TYPE>::ArraySlist(int mn)
{Setup(mn);
}
template<class TYPE>
void ArraySlist<TYPE>::Setup(int mn)
{nodes_used = 0;
nodes = (Snode<TYPE> *)(new char[mn * sizeof(Snode<TYPE>)]);
max_nodes = (nodes == 0) ? 0 : mn;
}
template<class TYPE>
Snode<TYPE> *ArraySlist<TYPE>::AllocNode(const TYPE &x)
{Snode<TYPE> *p = 0; // Default to failure
if (!free_list.IsEmpty()) {p = free_list.RmvFront();
}
else if (nodes_used < max_nodes) {p = nodes + nodes_used++;
}
if_(p)_new(p) Snode<TYPE>(x); // Use in-place construction
return p;
}
template<class TYPE>
void ArraySlist<TYPE>::FreeNode(Snodeb *n)
{typedef Snode<TYPE> typenode; // This typing helps some compilers
typenode *p = (typenode *)n;
p->typenode::~typenode(); // Explicitly destroy node
free_list.AttachToFront(p); // Attach to the free list
}
Figure 8.15 A sample ArraySlist object.

template<class TYPE>
ArraySlist<TYPE>::~ArraySlist()
{Clear();
delete[] (char *)nodes;
}
template<class TYPE>
void ArraySlist<TYPE>::Clear()
{typedef Snode<TYPE> typenode;
typenode *q, *p;
p = Front( );
while(!IsHeader(p)) { // For each node in useq = p->Next();
p->typenode::~typenode(); // Explicitly destroy node
p = q;
}
// The list is now made to appear empty, so that when the
// base class destructor calls Clear(), it works properly.
// Note that both the main and free lists are made empty.
MakeEmpty();
}
Cursor-Based Singly-Linked Lists
template<class TYPE>
class Snode {TYPE info;
unsigned next; // Index, or cursor, to next node
};
Figure 8.16 A sample cursor-based singly-linked list.

 Smaller. Depending on the implementation, a cursor may occupy less room than a pointer. For instance, a cursor might be an 8- or 16-bit integer, whereas a pointer will probably be either 16 or 32 bits. Thus, cursor-based linked lists can be more compact than those using pointers.
Smaller. Depending on the implementation, a cursor may occupy less room than a pointer. For instance, a cursor might be an 8- or 16-bit integer, whereas a pointer will probably be either 16 or 32 bits. Thus, cursor-based linked lists can be more compact than those using pointers. Relocatable. Since cursors are indexes relative to the beginning of the array, the array can be relocated elsewhere in memory--without having to update the cursors. If pointers are used instead for links, they would all have to be modified to reflect the new locations of the nodes.
Relocatable. Since cursors are indexes relative to the beginning of the array, the array can be relocated elsewhere in memory--without having to update the cursors. If pointers are used instead for links, they would all have to be modified to reflect the new locations of the nodes.template<class TYPE>
class CursorSlist {protected:
TYPE *info; // The node data array
unsigned *next; // Next cursors (next[0] == front)
unsigned num_nodes; // Number of nodes allocated
unsigned back; // Cursor to back of list
unsigned avail; // Cursor to front of avail list
void InsertAfter(unsigned p, unsigned x);
unsigned RmvNext(unsigned p);
int Alloc(int n);
void MakeEmpty();
public:
CursorSlist(int n);
unsigned Next(unsigned p) const;
unsigned AddAfter(const TYPE &x, unsigned p);
int DelNext(unsigned p);
TYPE &operator[](unsigned p);
// ... Other functions
};
Figure 8.17 Using parallel arrays to represent a singly-linked list.

template<class TYPE>
int CursorSlist<TYPE>::Alloc(int n)
// Allocates room for n list nodes
{// Create unconstructed array for the node data
info = (TYPE *) new char[n * sizeof(TYPE)];
if (!info) return 0; // Out of memory
// Create the next cursor array. Leave room for the
// header element.
next = new unsigned[n+1];
if (!next) {delete[] (char *)info;
return 0; // Out of memory
}
// Set up all nodes on the free list
// Boundaries handled after loop
for(unsigned i = 1; i<n+1; i++) next[i] = i+1;
avail = 1; // Starting cursor of the free list
next[n] = 0; // Null-terminate the free list
MakeEmpty(); // Start the main list to be empty
num_nodes = n;
return 1; // Successful
}
template<class TYPE>
void CursorSlist<TYPE>::MakeEmpty()
// Makes the list empty by pointing header to
// itself and pointing back to the header, too
{next[0] = 0;
back = 0;
}
Figure 8.18 An empty CursorSlist object.
template<class TYPE>
void CursorSlist<TYPE>::InsertAfter(unsigned p, unsigned x)
// Inserts a node indexed by x after node indexed by p.
{next[x] = next[p];
next[p] = x;
if (p == back) back = x;
}
template<class TYPE>
unsigned CursorSlist<TYPE>::AddAfter(const TYPE &x, unsigned p)
// Grabs a node from the free list, copies data x into it,
// and adds the node after node indexed by p
{unsigned n = avail; // Get cursor to next avail node
if (n == 0) return 0; // No room
avail = next[avail]; // One less node available
InsertAfter(p, n); // Insert node into main list
new(info + n - 1) TYPE(x); // In-place copy construction
return n; // Return cursor the node
}
template<class TYPE>
unsigned CursorSlist<TYPE>::RmvNext(unsigned p)
// Removes from the main list the node
// following the node indexed by p
{unsigned n = next[p]; // Like n = p->next
next[p] = next[n]; // Like p->next = n->next
if (n == back) back = p;
return n;
}
template<class TYPE>
int CursorSlist<TYPE>::DelNext(unsigned p)
// Removes the node following the node indexed by p, placing
// the node on the free list. The node data is destroyed.
{if (next[p] == 0) return 0; // Can't remove header
unsigned n = RmvNext(p); // Detach from list
(info + n - 1)->TYPE::~TYPE(); // Destroy node data
next[n] = avail; // Add to front of free list
avail = n; // New free list header
return 1; // Indicate success
}
Table 8.2 Different techniques for node insertions.
Cursor-Based Pointer-Based
next[x] = p; x->next = p;
next[p] = x; p->next = x;
Figure 8.19 A non-empty CursorSlist object.
template<class TYPE>
TYPE &CursorSlist<TYPE>::operator[](unsigned p)
{return info[p-1];
}
unsigned p = mylist.Front();
While(!mylist.IsHeader(p)) {cout << mylist[p] << ' - ';
p = mylist.Next(p);
}
template<class TYPE>
unsigned CursorSlist<TYPE>::Next(unsigned p) const
{return next[p];
}
Figure 8.20 A non-empty CursorDlist object.
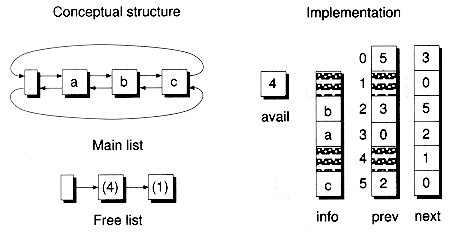
Cursor-Based Doubly-Linked Lists
template<class TYPE>
class CursorDlist {protected:
TYPE *info; // The node data array
unsigned *prev; // Prev cursors
unsigned *next; // Next cursors
unsigned avail; // Cursor to front of avail list
unsigned num_nodes; // Number of nodes allocated
void InsertAfter(unsigned p, unsigned x);
void InsertBefore(unsigned p, unsigned x);
unsigned Rmv(unsigned p);
...
};

template<class TYPE>
void CursorDlist<TYPE>::InsertBefore(unsigned p, unsigned x)
// Inserts a node indexed by x, assumed to be already
// detached from the free list, before node indexed by p
{prev[x] = prev[p]; // Like x->prev = p->prev
next[prev[p]] = x; // Like p->prev->next = x
next[x] = p; // Like x->next = p
prev[p] = x; // Like p->prev = x
}
template<class TYPE>
void CursorDlist<TYPE>::InsertAfter(unsigned p, unsigned x)
// Inserts a node indexed by x, assumed to be already
// detached from the free list, after node indexed by p
{next[x] = next[p]; // Like x->next = p->next
prev[next[p]] = x; // Like p->next->prev = x
prev[x] = p; // Like x->prev = p
next[p] = x; // Like p->next = x
}
template<class TYPE>
unsigned CursorDlist<TYPE>::Rmv(unsigned p)
// Removes the node indexed by p from the main list
{next[prev[p]] = next[p]; // Like p->prev->next = p->next
prev[next[p]] = prev[p]; // Like p->next->prev = p->prev
return p;
}
SUMMARY


