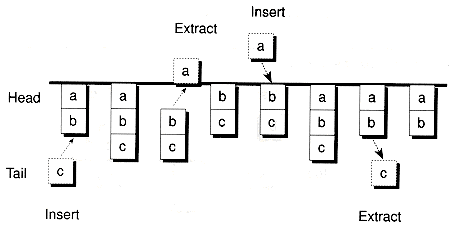
Stacks and queues are related data structures. Both are sequences of elements with restricted access. A stack is known as a last-in, first-out (LIFO) structure, where access to the elements takes place at one end of the sequence (called the top), using the operations push and pop. Figure 9.1 shows an example of a stack. A queue is a sequence where elements are inserted at one end (the tail), and extracted from the other end (the head). Queues work in a first-in, first out (FIFO) manner, as illustrated in Figure 9.2. Lines of cars at a traffic light, lines at the post office, and computer jobs waiting to be printed are all conceptual examples of queues.
It's possible to combine a stack and queue to arrive at another data structure, which we'll call a staque. (This terminology was invented by the author.) In a staque, the stack operations push and pop are defined, as well as the queue operations insert (into the tail) and extract (from the front.) Of course, the extract operation is identical to the pop operation.
By taking this approach one step further, we could also allow extraction from the tail. The result is known as a double-ended queue, or deque. Figure 9.3 shows an example of a deque.
A priority queue is another variation of a queue. Here, the elements are ordered by priorities that have been assigned to them, rather than by the order in which the elements are inserted. Figure 9.4 shows an example of a prioriity queue, with numbers representing the priority order. Notice that the sequence of elements are in descending order. You'll see priority queues implemented in Chapters 12. See also the companion volume [Flamig 93].
We'll now take a detailed look at stacks and queues, starting with fixed-size stacks.
The most common type of stack is a fixed-size stack, implemented as an array of elements. When you define array-based stacks, you need to consider these three main design issues:
The first issue can be handled quite easily. As we did for the arrays defined in Chapter 4, a base class can be defined that purposely avoids specifying how the stack elements are allocated. Then, we can derive specific classes for both statically and dynamically allocated stacks.
You can take two basic approaches to resolve the second issue (keeping track of the top and bounds of the stack). One approach is to use an index to indicate which element is at the top of the stack. When doing pushing and popping, this index can be checked with the bounds of the stack. This is the approach used in most books to implement array-based stacks. (Indeed, we used this approach in Chapters 3.) However, an index is not the best way to push and pop stack elements because subscripting involves multiplication and addition. A more efficient approach is to use pointers, both to reference the top of the stack and to mark the bounds of the stack.
You can also take two approaches to resolve the third issue (determining when to construct and deconstruct stack elements). The easiest approach is to construct the elements using default constructor calls when the stack is first built, and to destroy all the elements when the stack itself is destroyed. Indeed, that's the conventional way that C++ handles arrays. The second approach is to construct the stack elements individually during push operations, and to destroy elements one at a time during pop operations. This can be done using in-place copy constructor calls and explicit destructor calls--the same techniques we used for the variable-length arrays in Chapter 4.
Why bother with the in-place construction method? It's intuitively appealing and, in some cases, more correct to construct elements only when they are used. For example, constructed elements might use other resources (such as open file handles), allocate memory buffers, and so on. By deferring construction until the element is actually used, and destroying the element after it's no longer needed, you can ensure that the resources used by the element are acquired and freed in a timely fashion.
The types of constructors available can help you determine whether to use in-place construction. It may not make sense for the element type to have a default constructor (perhaps there is no sensible notion of a "null" object of that type). In this case, in-place construction is the best choice. Of course, for in-place construction to be used, the type must have a copy constructor, something that may not always be desirable either.
Using the preceding design principles, we'll now define a base class, ArrStk, which handles the basic operations of a fixed-sized array-based stack. The class assumes the stack elements are allocated elsewhere:
Complete code for the ArrStk class is given on disk in the files arrstk.h, arrstk.mth, and placenew.h. Through the use of defined macros, the code on disk can handle both the in-place copy-construction method and the conventional default-construction method. In this book, we show only the in-place construction method.
The ArrStk constructor takes a pointer to the stack elements (assumed to be already allocated, but not constructed) and the number of elements allocated. The Setup( ) function does all the work:
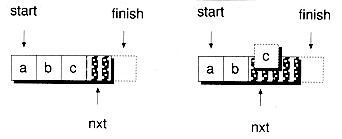
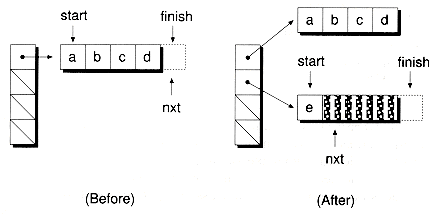
The Setup( ) function initializes the three pointers start, nxt, and finish, and the maximum stack size dimlen. The start and finish pointers mark the beginning and end of the stack, where finish actually points one element past the end. The nxt pointer references the next available stack element. The top of the stack--that is, the previous element pushed--can be found at nxt-1. When nxt equals start, the stack is empty. When nxt equals finish, the stack is full. Figure 9.5 shows the arrangement of an ArrStk object at various stages.
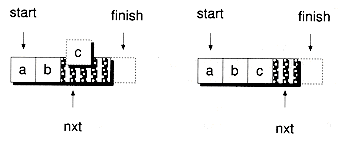
An element is pushed onto the stack by copy-constructing the data in place, at the location referenced by nxt, and then incrementing the nxt pointer, as given in the following Push( ) function. Figure 9.6(a) illustrates the pushing process.
The Pop( ) function works in reverse, first decrementing the nxt pointer and then invoking an explicit destructor call. Figure 9.6(b) illustrates the popping process.
Both Push( ) and Pop( ) check to make sure the bounds of the stack aren't violated. To optimize speed, you may want to forgo these checks--but only if this is warranted! The following FastPush( ) and FastPop( ) functions are provided to bypass the stack checks. These functions can be easily inlined:
It's interesting to compare in-place construction and explicit destruction with the conventional method, where all elements remain constructed during the stack's life. Here's how FastPush( ) and FastPop( ) would be coded for the latter:
You can see that the in-place construction used during a push is replaced by an assignment and that the code for a pop is the same as before, except no destructor call is made. For many element types, an assignment and a copy construction involve roughly the same amount of work. Thus, the push operation will take basically the same amount of time regardless of the method used. For pop operations, more work is being done in the extra destructor call for the in-place construction method. The data type being stored determines whether this is a problem or whether the reverse situation (not doing a destructor call) is a problem.
The in-place construction method provides the most rigorous design and is probably worth using, even if there is a slight performance penalty. Of course, for built-in types, this is a moot point since copy construction reduces to an assignment, and the destructor becomes a no-op.
The Rewind( ) function is related to Pop( ), and lets you unpop n elements off the stack:
Unlike Pop( ), the Rewind( ) function doesn't copy and pass back the data being popped from the stack. The data is simply discarded and destroyed. The Rewind( ) function can be used to clear the stack by unpopping all the elements. By convention, passing a number 0 to Rewind( ) (the default) results in the stack being cleared.
History( ) is another related function, and lets you inspect the element n positions back into the stack:
In the strictest sense, History( ) violates the rules of a stack. However, this function can be quite useful, when stacks are used in conjunction with tree-traversal algorithms. In the case of n = 0, the top element of the stack is inspected. The Top( ) function provides an efficient form for this special case:
To make ArrStk a concrete data type, we also provide an overloaded assignment operator to allow stacks to be copied. This operator function calls Copy( ) to do most of the work:
The Copy( ) function doesn't change the dimensioned length of the stack and, for that reason, a truncation may result during the copy.
You'll notice that a copy constructor is defined for ArrStk, but it is placed in the private section of the class. The constructor body (not shown) is actually empty. This approach prevents the user from trying to create a stack via copy construction. As defined, the ArrStk class is not responsible for allocating the stack elements, so it can't allocate a new stack to hold a copy of another stack. Likewise, a virtual destructor is defined in ArrStk, but it does nothing. It's up to the derived classes to handle the de-allocation of the stack elements.
The remaining ArrStk functions are those that determine the maximum size of the stack and whether the stack is empty or full:
With the ArrStk class now defined, it's easy to derive a new class, SarrStk, that allocates the stack elements statically:
The SarrStk class uses the same strategy that was used for the statically allocated, variable-length arrays in Chapter 4. The stack elements are allocated and de-allocated as an array of characters. This approach defers the construction of the elements until they are actually used, and prevents them from being destroyed twice when the stack itself is destroyed. Here is one of the constructors, and the destructor, to illustrate this technique. In the destructor, the stack must be rewound so that we can call the destructors for all elements in use:
Complete code for the SarrStk class is given on disk in the file sarrstk.h. A test program tstsastk.cpp is also provided.
The DarrStk class defines stacks that are dynamically allocated. As was done with the SarrStk class, we use a typecasting trick so that the stack elements can be allocated without being constructed at the same time. This next class definition, followed by one of the constructors and the destructor, illustrates the technique. This time, the destructor must not only rewind the stack, but also must delete the elements:
Complete code for the DarrStk class is given on disk in the file darrstk.h. The test program tstdastk.cpp is also provided.
Fixed-size, array-based stacks provide the most efficient form of stack; however, it can be inconvenient to fix the size of the stack. A linked list is the obvious candidate to implement a resizable stack. We provided examples of this in Chapter 3. Unfortunately, when we use a linked list, a new node must be allocated from the heap with every push, and a node must be de-allocated with every pop. For some heap-implementations, this can be a time-consuming process. In Chapter 8, we demonstrated one way around this problem: implement an auxiliary list to cache nodes that would otherwise be freed.
A resizable array, as implemented in Chapter 4, provides another alternative. However, this approach presents a problem: each time the array grows beyond its allocated bounds, it has to be copied into a new location that has more room.
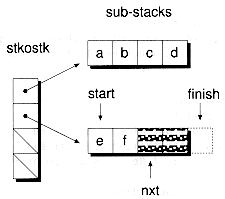
There is an array-based solution that's better than all of the alternatives just presented. The idea is based on working with multiple stacks. As a stack becomes full, a switch is made to a new stack. As a stack becomes empty, a switch is made back to a previously used stack. This type of resizable stack can be implemented using a stack-of-stacks. Initially, the stack-of-stacks is empty. When the first element is to be added, a new substack is allocated and a pointer to it is pushed onto the stack-of-stacks. When the first substack becomes full, another substack is allocated and its pointer is pushed onto the stack-of-stacks. As elements are removed and a substack becomes empty, the substack is popped from the stack-of-stacks.
You can implement a stack-of-stacks using the DarrStk template, with the element type being the DarrStk type itself. In the following example, we'll declare such a stack, with room to hold mxstks substacks:
When stkostk is first allocated, the individual substacks remain unconstructed. As a result, the only space initially occupied by stkostk is the space for the instance variables of DarrStk (start, finish, nxt, and dimlen) multiplied mxstks times. Substacks are constructed only when elements are pushed onto the stack. Here's how an element x of type TYPE can be pushed onto and popped from the stack:
A working example of a stack-of-stacks is given on disk in the file stkostk.cpp.
The nested template, stack-of-stacks approach works fine, but some stack operations--such as Rewind( ) and History( )--are somewhat difficult to implement under this approach. For this reason, we'll implement a stack-of-stacks more directly, using the following RarrStk class:
Complete code for the RarrStk class is given in the files rarrstk.h and rarrstk.mth. A test program is provided in the file tstrastk.cpp.
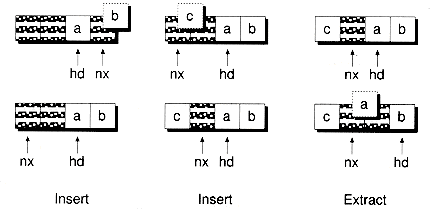
A RarrStk object is made up of an array of stack pointers called stkostk and one or more substacks. Each substack is allocated and de-allocated separately as needed, and stkostk keeps track of their locations. As is true with the ArrStk class, RarrStk uses the pointers nxt, start, and finish, but this time they point to elements in the current substack. When a switch is made to another substack, these pointers are modified accordingly. Figure 9.7 shows an example of a RarrStk object with two substacks allocated (but with room for four stacks).
The RarrStk constructor, which calls Setup( ), creates an empty stack with no substacks allocated, and the stkostk array is initialized to hold null pointers.
When calling the constructor, you specify the size of each substack and the number of substacks that you wish to allow. Note that a RarrStk object does have a maximum size (equal to stksixe * maxstks), but unlike an ArrStk object, this size doesn't affect the initial amount of memory reserved. Initially, RarrStk only requires enough room to store the stkostk array of pointers.
Elements are pushed on the stack in the same way that we used previously, with one exception: if the current substack is full, a new substack is started. Figure 9.8 illustrates this process. The following Push( ) and PushStk( ) routines show how the pushing is done. You'll notice that in-place construction is used for the new element:
The PushStk( ) routine--responsible for ensuring that a new substack gets allocated--is somewhat tricky. First, the substack may already be allocated (more on this later), which we determine by checking for a non-null pointer in stkostk. Second, since we're using in-place construction, the new substack is allocated as an array of characters to prevent the element constructors from being called prematurely. Note how the variable nxtstk keeps track of the next available location in stkostk, and how it's possible for stkostk to become completely full.
Popping an element from the stack uses the reverse approach. If the current substack becomes empty when an element is popped off the stack, the sub-stack can be de-allocated. However, the substack shouldn't be de-allocated immediately. You should postpone the de-allocation to avoid the "thrashing" that can occur at the boundary of a substack. Consider what would happen if the first element of a substack is popped and a new element is then immediately pushed. If the substack were de-allocated as soon as it became empty, it would have to be immediately re-allocated when a new element is added. To avoid this, the following Pop( ) function de-allocates a substack only when the one precedes it becomes empty. When a substack is ready to be freed, the PopStk( ) function is called. Figure 9.9 illustrates the process.
The RarrStk class contains a full complement of constructors, a destructor, and an overloaded assignment operator. As is the case with the ArrStk class, RarrStk includes functions like IsEmpty( ), IsFull( ), History( ), Top( ), Rewind( ), and so on. The details of these functions are given on disk.
Stacks based on the RarrStk class are quite efficient, but they are slightly slower than those based on ArrStk--due to the need to allocate and de-allocate sub-stacks. This problem can be alleviated by increasing the size of the blocks, and thus reducing the frequency of substack allocations. Note that RarrStk objects are significantly faster than a linked list approach. The RarrStk objects also occupy less space, since each element doesn't need an extra link pointer. The only disadvantage is a slight increase in the code required (which could be magnified if many classes are instantiated from the template).
To allow you to compare RarrStk objects with linked-list based stacks, we've provided the following additional files on disk: liststk.h, liststk.mth, tstlstk.cpp, and stktimer.cpp. The latter program tests the runtime efficiency of the two approaches.
We'll now focus on the implementations of queues. We'll begin by discussing list-based queues, since they are the easiest to implement. Next, we'll look at compact array-based implementations. Recall that, with a queue, elements are inserted at the rear of the queue and extracted from the front. A singly-linked list with a back pointer can handle these operations quite nicely. There are different methods we could use:
1. Implement a linked-list queue class from scratch. This is the most direct method. However, with this approach we must duplicate a lot of list functionality that could be reused for other lists.
2. Use the Slist class of Chapter 8 as is, without creating a special queue version. We can use functions like AddToBack( ) and DelFront( ) to support the queue operations. However, all the other list operations are available as well, such as DelNext( ), which violate restricted access to the ends of the queue. Whether this is a problem depends on how strictly you wish to follow the definition for a queue.
3. A queue-specific class template can be derived from the Slist class. We can use private derivation, and thus control which list functions are available. By using inline functions, we can change the names of AddToBack( ) and DelFront( ) to more high-level names such as Insert( ) and Extract( ). This approach gets messy because an extra template class, Slist, must be instantiated, plus we run into all sorts of protected-access problems. Of course, if you need the Slist class for some other part of your program, this approach may be best since you'll be reusing the Slist class.
4. A queue-specific class template can be derived from the Slistb base class. This represents a compromise of the other three approaches. By deriving from Slistb, we allow much of the code to be reused. Yet, because the derivation is direct, we'll have a simpler implementation than if we had used the Slist class.
For this book, we've chosen the fourth method, since it is perhaps the best engineering tradeoff. However, the method that works best for you might depend on a lot of factors; don't hesitate to implement queues using your own methods.
We can derive a ListQ class from Slistb, whose purpose is to implement listbased queues:
Complete code for the ListQ class is given on disk in the files listq.h, listq.mth, and snode.h. A test program is given in tstlq.cpp.
The ListQ class is very similar to the Slist class, but has fewer functions. For instance, we chose not to support queue concatenations, even though this might be useful in some cases. As was true with the Slist class, ListQ allocates nodes on the heap. We could, of course, use the free-list technique for node caching or use array-based allocation.
The most important functions of ListQ are Insert( ) and Extract( ), which implement the basic queue operations:
The Insert( ) and Extract( ) functions use the AttachToBack( ) and RmvFront( ) functions of Slistb, as well as the virtual functions FreeNode( ) and AllocNode( ).
Sometimes it's useful to peek at the front element in the queue without actually removing it. The Head( ) function is used for that purpose:
Figure 9.10 illustrates the process of adding and removing elements from a ListQ object.
You can add stack-like operations to the ListQ class and derive a combination stack and queue (staque) class. Alternatively, you can derive the staque class from a stack class or, by using multiple inheritance, combine a stack and queue class. In the first case, the Pop( ) function would be identical to Exctract( ) and the Push( ) operation could be implemented by making a call to the AddToFront( ) function of Slistb. The details for this are given on disk.
Complete code for a list-based staque class, ListSQ, is given on disk in the files listsq.h and listsq.mth. This class is derived from a list-based stack class, ListStk, which is given in the files liststk.h and liststk.mth. A test program is provided in tstlsq.cpp.
Here, a singly-linked list with a back pointer isn't quite up to the job. The problem is that we can't efficiently remove the last node from the list, because we must scan the list from beginning to end to find the node immediately preceding the last one.
You can either choose to accept this inefficiency or use a doubly-linked list. Of course, a doubly-linked list has its own inefficiency, costing an extra pointer per node. As always, you are faced with the classic speed versus space tradeoff. Here, sacrificing space for speed is probably the better choice. The space required by a queue is rarely an issue. However, the speed to remove an element might be. (If space is an issue, an array-based queue is a better approach, as you'll see later on.)
By using the doubly-linked list approach, we can implement a deque with the following ListDQ class, which is derived from Dlistb:
Complete code for the ListDQ class is given in the files listdq.h, listdq.mth, and dnode.h. A test program is provided in the file tstldq.cpp.
The design of the ListDQ class is similar to ListQ, but splits the Insert( ) and Exctract( ) functions into four functions-InsertHead( ), InsertTail( ), ExtractHead( ), and ExtractTail( ):
List-based queues are especially useful because you don't have to pre-allocate storage for the maximum size of the queue. However, if the queues you are using tend to be of some fixed size, then arrays offer more compact representations. Such array-based queues will be discussed next.
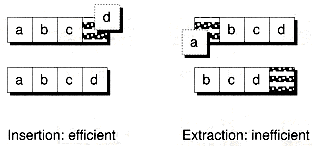
The simplest way to implement an array-based queue is to have the first element of the array be the head of the queue, and utilize a pointer to the tail of the queue. It's easy to insert an element into this type of queue. We simply increment the tail pointer to the next available slot. However, we run into a problem in extracting from the front of the queue, because doing so means all remaining elements of the array must be shifted up--a time-consuming process. Figure 9.11 illustrates this inefficiency.
An alternative is to use a chasing pointer technique. The idea is to add another pointer to the head of the queue. The head pointer is initialized to the start of the array. As elements are inserted, the tail pointer is incremented. As elements are extracted, the head pointer is incremented, chasing the tail pointer. With this strategy, both insertion and extraction are efficient, as illustrated in Figure 9.12.
The chasing pointer technique does present some problems. As elements are extracted, the storage space at the beginning of the array is discarded and never reused. Also, the head and tail pointers are always incremented (but never decremented). Thus, even if the number of extractions equals the number of insertions, the array eventually runs out of space.
To solve these problems, we can use a circular array, also called a ring buffer. In such an array, the end wraps around to the beginning. Circular arrays don't physically exist. Instead, they are simulated by using normal linear arrays, where all pointers or indexes scanning the array are reset to the starting element when the ending element has been passed. Figure 9.13 illustrates this wraparound effect.
Next, we'll develop an array-based queue class, ArrQ, that uses the circular array technique. The design for this class is very similar to the ArrStk class, in the following ways:
Here is the ArrQ class definition:
Complete code for the ArrQ class is given on disk in the files arrq.h and arrq.mth. Static and dynamic derived classes are given in the files sarrq.h and darrq.h. Test programs can be found in the files tstsaq.cpp and tstdaq.cpp.
Four pointers are used to represent the queue. The variable st points to the starting element in the array, fn points to the last element in the array, hd points to the logical start of the queue, and nx points to the next element available for insertions. The tail of the queue can be found at location nx-1. The ArrQ constructor sets up these pointers by calling Setup( ).
Figure 9.14(a) shows the configuration of an empty queue as created by Setup( ). Note how the nx and hd pointers are equal at this stage. The condition nx==hd is one way to test for an empty queue. However, this condition also occurs when the queue is full, as illustrated by Figure 9.14(b).
We can solve this ambiguity in two ways. Under one approach, we never let the array fill up entirely, holding the last remaining element in reserve. (The location of this element rotates through the array as the queue is accessed.) In this scheme, when nx ==hd-1, the queue is said to be full. Unfortunately, the reserved element represents wasted space, which can be costly if the array elements are large. Under the second approach, we maintain a flag (which we call isfull) that is set when the queue becomes full during an insertion and reset as elements are extracted. The following IsEmpty( ) and IsFull( ) functions show how the isfull flag resolves the empty/full ambiguity:
By maintaining the isfull flag, we avoid wasting one of the array elements, but we do create some complications. Here are the Insert( ) and Extract( ) functions, which illustrate how the hd and nx pointers are updated, and how the isfull flag is maintained:
The functions Inc( ) and Dec( ) are used to conveniently wrap the pointers around when we reach the ends of the array:
We can now derive a new class that adds stack-like operations to the ArrQ class, similar to the way used for list-based stacks. Such a class, ArrSQ, is given on disk.
Complete code for an array-based staque class is given on disk in the files arrsq.h and arrsq.mth. Static and dynamic versions, SarrSQ and DarrSQ, are provided in the files sarrsq.h and darrsq.h. Two test programs are provided in tstsasq.cpp and tstdasq.cpp.
A double-ended queue class is easy to derive from ArrQ, as the following ArrDQ class shows:
Complete code for the ArrDQ class is given on disk in the files arrdq.h and arrdq.mth. Static and dynamic classes, SarrDQ and DarrDQ, are given in the files sarrdq.h and darrdq.h. Test programs are provided in the files tstsadq.cpp and tstdadq.cpp.
The Insert( ) and Extract( ) functions of the ArrQ class are replaced by InsertHead( ), InsertTail( ), ExtractHead( ), and ExtractTail( ).
Note that we could have derived the ArrDQ class from the ArrSQ class, since we would only need to add the function to remove elements from the end of the queue. We chose not to do this because the chain of template-based derivations (ArrQ to ArrSQ to ArrDQ to SarrDQ and DarrDQ) starts to get a little unwieldy. The derivation of ArrDQ directly from ArrQ eliminates one class from this chain.
The discussion so far has implicitly assumed that the stacks and queues store only one kind of object, and are thus homogenous. However, you will probably have situations where it is useful to store different types of objects. Any of the techniques given earlier in Chapters 5 and 8 for creating heterogenous arrays and linked-lists could also be used for stacks and queues. As always, you can accomplish this by storing indirect pointers to objects, perhaps using reference-counted smart pointers to provide the safest designs.
In this chapter, you've seen how to efficiently implement stacks and queues by using two opposing data structures: arrays and linked lists. Both forms offer advantages. Linked lists allow more flexibility for variable stack and queue lengths, while arrays offer more compact representations when a fixed size is acceptable. The RarrStk class provides a very efficient implementation of resizable stacks by using a stack-of-stacks. Note that resizable array-based queues could be implemented in a way similar to the RarrStk class, using a queue of queues. The details are somewhat messy, though, because the deferred allocation and deallocation of the subqueues must be handled in both directions.
Perhaps the most important design feature presented in this chapter is the use of in-place construction and explicit destruction of elements when they are added and removed from the stacks and queues. Most texts on C++ do not mention this technique, yet in-place construction does lead to a more robust design.
Figure 9.3 A Double-ended queue.
FIXED-SIZE STACKS
Should the stack be statically or dynamically allocated? How should you keep track of the top of the stack and the bounds of the stack? When should the stack elements be constructed and destructed?Figure 9.4 A priority queue.
A Base Class for Array-Based Stacks
template<class TYPE>
class ArrStk {protected:
TYPE *start, *finish, *nxt;
unsigned dimlen;
void Setup(TYPE *m, unsigned n);
ArrStk(const ArrStk<TYPE> &);
public:
ArrStk(TYPE *m, unsigned n);
virtual ~ArrStk( );
void operator=(const ArrStk<TYPE> &s);
void Copy(const ArrStk<TYPE> &s);
int Push(const TYPE &x);
int Pop(TYPE &x);
int Pop( );
void FastPush(const TYPE &x);
void FastPop(TYPE &x);
TYPE *Top( );
const TYPE *Top( ) const;
TYPE *History(unsigned n);
const TYPE *History(unsigned n) const;
void Rewind(unsigned n=0);
int IsFull( ) const;
int IsEmpty( ) const;
unsigned Size( ) const;
};
template<class TYPE>
ArrStk<TYPE>::ArrStk(TYPE *m, unsigned n)
// Sets up a stack with n already-allocated elements
// pointed to by m
{Setup(m, n);
}
template<class TYPE>
void ArrStk<TYPE>::Setup(TYPE *m, unsigned n)
{start = m;
nxt = start;
if (start) { // Was memory actually allocated?finish = start + n;
dimlen = n;
}
else {finish = start;
dimlen = 0;
}
}
template<class TYPE>
int ArrStk<TYPE>::Push(const TYPE &x)
// Pushes a copy of x onto the stack unless
// stack is full. Returns 1 if not full;returns 0 otherwise.
{if (!IsFull( )) {new(nxt++) TYPE(x); // In-place copy construction
return 1;
}
else return 0;
}
template<class TYPE>
int ArrStk<TYPE>::Pop(TYPE &x)
// Pops the top element from the stack, returning
// a copy of it in x, unless stack is empty. Returns 1
// if stack wasn't empty before the pop; otherwise, returns 0.
{if (!IsEmpty( )) {x = *(--nxt); // Make a copy
nxt->TYPE::~TYPE( ); // Explicit destruction
return 1;
}
else return 0;
}
Figure 9.5 An ArrStk object at various stages.
(a) Empty
(b) With two elements
(c) Full
Figure 9.6 Using an ArrStk object.
(a) Pushing
(b) Popping
template<class TYPE>
void ArrStk<TYPE>::FastPush(const TYPE &x)
// For fastest, but unsafest pushes.
{new(nxt++) TYPE(x); // In-place copy construction
}
template<class TYPE>
void ArrStk<TYPE>::FastPop(TYPE &x)
// For fastest, but unsafest pops.
{x = *(--nxt); // Make a copy
nxt->TYPE::~TYPE( ); // Explicit destruction
}
template<class TYPE>
void ArrStk<TYPE>::FastPush(const TYPE &x)
// If in-place construction isn't being used
// (assumes element already constructed)
{x = *nxt++;
}
template<class TYPE>
void ArrStk<TYPE>::FastPop(TYPE &x)
// If in-place construction isn't being used
// (assumes element to remain constructed)
{x = *(--nxt);
}
template<class TYPE>
void ArrStk<TYPE>::Rewind(unsigned n)
{if (n == 0) n = dimlen; // Ensures all elements popped
// Explicit destructor called for each element popped
while(n-- && nxt != start) (--nxt)->TYPE::~TYPE();
}
template<class TYPE>
TYPE *ArrStk<TYPE>::History(unsigned n)
{if (IsEmpty( )) return 0;
TYPE *p = nxt-l;
while(1) {if (n-- == 0) return p; // Found the element
if (p-- == start) return 0; // Out of range
}
}
template<class TYPE>
TYPE *ArrStk<TYPE>::Top()
{return IsEmpty() ? 0 : (nxt-1);
}
template<class TYPE>
void ArrStk<TYPE>::operator=(const ArrStk<TYPE> &s)
// Traps assignment to self
{if (this != &s) Copy(s);
}
template<class TYPE>
void ArrStk<TYPE>::Copy(const ArrStk<TYPE> &s)
// Clears the stack, and then copies the elements
// of s onto the stack. Note that if s.dimlen >
// dimlen, not all elements will be copied.
{Rewind();
TYPE *t = s.start;
unsigned n = dimlen;
// Elements copied via in-place copy construction
while (n- && t != s.nxt) new(nxt++) TYPE(*t++);
}
template<class TYPE>
unsigned ArrStk<TYPE>::Size( ) const
{return dimlen;
}
template<class TYPE>
int ArrStk<TYPE>::IsEmpty( ) const
{return nxt == start;
}
template<class TYPE>
int ArrStk<TYPE> : : IsFull ( ) const
{return nxt == finish;
}
Statically Allocated Stacks
template<class TYPE, unsigned SIZE>
class SarrStk : public ArrStk<TYPE> {protected:
char elem[sizeof (TYPE)*SIZE]; // Notice the char type!
public:
SarrStk();
SarrStk (const ArrStk<TYPE> &s);
SarrStk (const SarrStk<TYPE, SIZE> &s);
virtual ~SarrStk ();
void operator=(const ArrStk<TYPE> &s);
} ;
template<class TYPE, unsigned SIZE>
SarrStk<TYPE, SIZE>: :SarrStk()
: ArrStk<TYPE>((TYPE *) elem, SIZE)
{// Nothing else to do
}
template<class TYPE, unsigned SIZE>
SarrStk<TYPE, SIZE>: :~SarrStk()
{Rewind();
}
Dynamically Allocated Stacks
template<class TYPE>
class DarrStk : public ArrStk<TYPE> {public:
DarrStk(unsigned n);
DarrStk(const ArrStk<TYPE> &s);
DarrStk(const DarrStk<TYPE> &s);
virtual ~DarrStk();
void operator=(const ArrStk<TYPE> &s);
};
template<class TYPE>
DarrStk<TYPE>: :DarrStk(unsigned n)
// Elements are allocated as an array of characters
// to defer their construction until needed
: ArrStk<TYPE>( (TYPE *)new char[sizeof(TYPE)*n], n)
{// Nothing else to do
}
template<class TYPE>
DarrStk<TYPE>::~DarrStk()
{Rewind();
// Elements are deleted as an array of characters,
// since that's how they were allocated
delete[] (char *)start;
}
RESIZABLE STACKS
Stacks of Stacks
DarrStk< DarrStk<TYPE> > stkostk (mxstks);
// Push function:
if (!stkostk.IsFull()) {if (stkostk.IsEmpty() || stkostk.Top()->IsFull()) {stkostk.Push(DarrStk<TYPE>(blksize));
}
return stkostk.Top() ->Push(x);
}
else return 0 ;
// Pop function:
if (!stkostk.IsEmpty()) {if (stkostk.Top()->IsEmpty()) {stkostk.Rewind(1);
if (stkostk.IsEmpty()) return 0;
}
return stkostk.Top( )->Pop(x);
}
else return 0;
The RarrStk Class
template<class TYPE>
class RarrStk {protected:
TYPE **stkostk; // Stack-of-stacks pointers
TYPE *nxt, *start, *finish; // Current stack variables
unsigned maxnelems, stksize, nxtstk, maxstks;
int Setup(unsigned nb);
int PushStk();
void PopStk(unsigned b);
void Dealloc();
public:
RarrStk(unsigned stksz, unsigned mxstks=1);
RarrStk(const RarrStk<TYPE> &s);
~RarrStk();
void operator=(const RarrStk<TYPE> &s);
int Copy(const RarrStk<TYPE> &s);
int Push(const TYPE &x);
int Pop(TYPE &x);
int Pop();
TYPE *Top();
const TYPE *Top() const;
TYPE *History (unsigned n);
const TYPE *History(unsigned n) const;
void Rewind(unsigned n = 0);
int IsFull() const;
int IsEmpty() const;
unsigned Size() const;
};
template<class TYPE>
RarrStk<TYPE>::RarrStk(unsigned stksz, unsigned mxstks)
{stksize = stksz;
Setup(mxstks);
}
template<class TYPE>
int RarrStk<TYPE>::Setup(unsigned ns)
{nxtstk = 0; nxt = 0; start = 0; finish = 0;
stkostk = new TYPE *[ns]; // Up to ns sub-stacks
if (stkostk) {maxstks = ns;
while(ns) stkostk[-ns] = 0;
}
else maxstks = 0;
maxnelems = stksize * maxstks;
return maxstks > 0;
}
Figure 9.7 A partially filled RarrStk object.
template<class TYPE>
int RarrStk<TYPE>::Push(const TYPE &x)
}
if (nxt == finish) { // Need another stackif (!PushStk()) return 0; // Couldn't allocate
}
new(nxt++) TYPE(x); // In-place copy construction
return 1; // Success
}
template<class TYPE>
int RarrStk<TYPE>::PushStk( )
// Ensures room has been allocated for the next highest
// stack (ie: stk # nxtstk.) Returns 1 if successful;
// returns 0 if unable to allocate.
{if (nxtstk == maxstks) return 0: // Table full
TYPE *p = stkostk[nxtstk];
if (p == 0) { // Block not already allocatedp = (TYPE *)new char[stksize*sizeof(TYPE)];
stkostk[nxtstk] = p; // Record stack pointer
}
// else stack still allocated from before
if (p) { // We have stack allocatednxt = start = p;
finish = p + stksize;
nxtstk++;
return 1;
}
else { // Allocation error, so leave everything alonereturn 0;
}
}
Figure 9.8 Pushing onto a RarrStk object.
template<class TYPE>
int RarrStk<TYPE>::Pop(TYPE &x)
// Pops the top element from the stack, returning
// a copy of it in x. Returns 1 if stack wasn't empty
// before push; otherwise, returns 0. If stack was empty, the
// data in x will be untouched.
{if (nxt == start) {// Pop next higher stack if this has not already been done
PopStk(nxtstk);
// Return if stack is empty, but note that there may
// still be a stack allocated (when nxtstk = 1)
if (nxtstk <= 1) return 0;
// Otherwise, we must move to end of lower stack
-nxtstk; // nxtstk guaranteed >= 1 after decrement
start = stkostk[nxtstk-1];
finish = start + stksize;
nxt = finish - 1;
}
else -nxt;
x = *nxt;
nxt->TYPE::~TYPE( );
return 1;
}
template<class TYPE>
void RarrStk<TYPE>::PopStk(unsigned b)
// De-allocates stack b if not already de-allocated,
// destructing elements along the way if INPLACECONST
// isn't true. Sets pointer in stack table
// to null. Does nothing if b is out of range.
{if (b >= maxstks) return; // b is out of range
if (stkostk[b] == 0) return;
delete[] (char *)(stkostk[b]);
stkostk[b] = 0;
}
Figure 9.9 Delayed de-allocation of a substack.
LIST-BASED QUEUES
template<class TYPE>
class ListQ : public Slistb {protected:
virtual Snode<TYPE> *AllocNode(const TYPE &x);
virtual Snodeb *DupNode(const Snodeb *n);
virtual void FreeNode(Snodeb *n);
public:
ListQ();
ListQ(const ListQ<TYPE> &s);
~ListQ();
void operator=(const ListQ<TYPE> &s);
int Extract(TYPE &x);
int Extract();
int Insert(const TYPE &x);
TYPE *Head();
const TYPE *Head() const;
int IsFull() const;
};
template<class TYPE>
int ListQ<TYPE>::Insert(const TYPE &x)
// Creates a new node having a copy of x for its data
// and puts in on the back of the queue. Returns 1
// if allocation successful; otherwise, returns 0.
{Snode<TYPE> *p = AllocNode(x);
if (p == 0) return 0;
AttachToBack(p);
return 1;
}
template<class TYPE>
int ListQ<TYPE>::Extract(TYPE &x)
// Gets the data from the front node of the queue and
// copies it into x. If queue is empty, x is left
// untouched and a 0 is returned; otherwise, returns a 1.
{Snode<TYPE> *p = (Snode<TYPE> *)RmvFront( );
if (p == 0) return 0;
x = p->info;
FreeNode(p);
return 1;
}
template<class TYPE>
TYPE *ListQ<TYPE>::Head( )
// Returns the data contained in the head node of the queue,
// or a null pointer if the queue is empty
{return IsEmpty() ? 0 : &(((Snode<TYPE> *)Front())->info);
}
LIST-BASED STAQUES
LIST-BASED DEQUES
Figure 9.10 Using a ListQ object.
template<class TYPE>
class ListDQ : public Dlistb {protected:
virtual Dnode<TYPE> *AllocNode (const TYPE &x);
virtual Dnodeb *DupNode(const Dnodeb *n);
virtual void FreeNode(Dnodeb *n);
public:
ListDQ();
ListDQ(const ListDQ<TYPE> &s);
~ListDQ();
void operator=(const ListDQ<TYPE> &s);
int ExtractHead(TYPE &x);
int ExtractTail(TYPE &x);
int InsertHead(const TYPE &x);
int InsertTail(const TYPE &x);
TYPE *Head();
const TYPE *Head() const;
TYPE *Tail();
const TYPE *Tail() const;
int IsFull() const;
};
template<class TYPE>
int ListDQ<TYPE>::InsertHead(const TYPE &x)
{Dnode<TYPE> *p = AllocNode(x);
if (p == 0) return 0;
AttachToFront(p);
return 1;
}
template<class TYPE>
int ListDQ<TYPE>::InsertTail(const TYPE &x)
{Dnode<TYPE> *p = AllocNode(x);
if (p == 0) return 0;
AttachToBack(p);
return 1;
}
template<class TYPE>
int ListDQ<TYPE>::ExtractHead(TYPE &x)
{Dnode<TYPE> *p = (Dnode<TYPE> *)RmvFront( );
if (p == 0) return 0;
x = p->info;
FreeNode(p);
return 1;
}
template<class TYPE>
int ListDQ<TYPE>::ExtractTail(TYPE &x)
{Dnode<TYPE> *p = (Dnode<TYPE> *)RmvBack( );
if (p == 0) return 0;
x = p->info;
FreeNode(p);
return 1;
}
ARRAY-BASED QUEUES
Figure 9.11 An inefficient array-based queue.
The ArrQ Class
The ArrQ class isn't responsible for allocating memory for the queue. The derived classes SarrQ and DarrQ determine whether the memory is allocated statically or dynamically. These classes are similar to SarrStk and DarrStk. Pointers are used to represent the head and tail of the queue, and also for the actual bounds of the underlying array. This is more efficient than using indexes, since we can avoid the multiplication needed by subscripting. In-place construction is used when elements are added and explicit destruction is used when elements are removed. This approach leads to a more rigorous and robust design. The class is a concrete data type implemented as a template, with the appropriate constructors, destructor, and overloaded assignment operator.Figure 9.12 An array-based queue with chasing pointers.
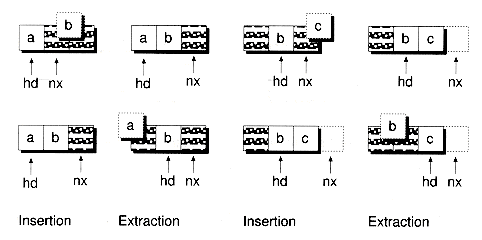
Figure 9.13 A circular array with wrapround pointers.
template<class TYPE>
class ArrQ {protected:
TYPE *st, // Pointer to start element
*fn, // Pointer to finish element
*hd, // Pointer to head element in the queue
*nx; // Pointer to next available element
int isfull; // Flag to indicate a full queue
unsigned dimlen; // Maximum number of elements
void Setup(TYPE *m, unsigned n);
ArrQ(const ArrQ<TYPE> &); // To disallow copy constructing
TYPE *Inc(TYPE *x) const;
TYPE *Dec(TYPE *x) const;
public:
ArrQ(TYPE *m, unsigned n);
virtual ~ArrQ();
void operator=(const ArrQ<TYPE> &s);
int Copy(const ArrQ<TYPE> &s);
void Clear();
int Extract(TYPE &x);
int Extract();
int Insert(const TYPE &x);
TYPE *Head();
const TYPE *Head() const;
int IsEmpty() const;
int IsFull() const;
unsigned Size() const;
};
template<class TYPE>
ArrQ<TYPE>::ArrQ(TYPE *m, unsigned n)
// Constructs a new queue with a maximum of n elements
// stored at location m, assumed to be already allocated
{Setup(m, n);
}
template<class TYPE>
void ArrQ<TYPE>::Setup(TYPE *m, unsigned n)
{st = m;
if (st && n) { // Array isn't nullfn = st+n-1;
dimlen = n;
isfull = 0;
}
else { // A null array, which is always 'full'fn = st;
dimlen = 0;
isfull = 1;
}
hd = st;
nx = st;
}
Figure 9.14 Ambiguous empty and full conditions.
(A) Empty
(B) Full
template<class TYPE>
int ArrQ<TYPE>::IsEmpty( ) const
{return hd == nx && !isfull;
}
template<class TYPE>
int ArrQ<TYPE>::IsFull( ) const
{return isfull;
}
template<class TYPE>
int ArrQ<TYPE>::Insert(const TYPE &x)
// Copies x into the next available element at the end
// of the queue. If queue is full, nothing happens.
{if (IsFull( )) return 0;
new(nx) TYPE(x);
nx = Inc(nx);
if (nx == hd) isfull = 1; // We just went full
return 1;
}
template<class TYPE>
int ArrQ<TYPE>::Extract(TYPE &x)
// Gets the data from the head element and stores a copy of
// it in x. Removes and possibly destroys the head element.
// If queue is empty, x is left untouched and a
// 0 is returned; otherwise, a 1 is returned.
{if (IsEmpty()) return 0;
x = *hd;
hd->TYPE::~TYPE();
hd = Inc(hd); // We have a new head
isfull = 0; // And we certainly can't be full anymore
return 1;
}
template<class TYPE>
TYPE *ArrQ<TYPE>::Inc(TYPE *x) const
// Increments a pointer and wraps around to
// the start if necessary
{return (x == fn) ? st : x+1;
}
template<class TYPE>
TYPE *ArrQ<TYPE>::Dec(TYPE *x) const
// Decrements a pointer, wrapping around to
// the end if necessary
{return (x == st) ? fn : x-1;
}
Array-Based Staques
The ArrDQ Class
template<class TYPE>
class ArrDQ : public ArrQ<TYPE> {protected:
ArrDQ(const ArrDQ<TYPE> &s);
public:
ArrDQ(TYPE *m, unsigned n);
void operator=(const ArrQ<TYPE> &s);
int ExtractHead(TYPE &x);
int ExtractTail(TYPE &x);
int InsertHead(const TYPE &x);
int InsertTail(const TYPE &x);
TYPE *Tail( );
const TYPE *Tail( ) const;
};
template<class TYPE>
int ArrDQ<TYPE>::InsertHead(const TYPE &x)
// Puts a new element at the front of the queue, holding
// a copy of x
{if (IsFull( )) return 0;
hd = Dec(hd);
new(hd) TYPE(x);
if (nx == hd) isfull = 1;
return 1;
}
template<class TYPE>
int ArrDQ<TYPE>::InsertTail(const TYPE &x)
// Puts a new element at the end of the queue, holding a
// copy of x
{return ArraQ<TYPE>::Insert(x);
}
template<class TYPE>
int ArrDQ<TYPE>::ExtractHead(TYPE &x)
// Copies the data of the front element into x and
// removes the element from the queue
{return ArrQ<TYPE>::Extract(x);
}
template<class TYPE>
int ArrDQ<TYPE>::ExtractTail(TYPE &x)
// Copies the data of the rear element into x and
// removes the element from the queue
{if (IsEmpty( )) return 0;
nx = Dec(nx);
x = *nx;
nx->TYPE::~TYPE( );
isfull = 0;
return 1;
}
HETEROGENOUS STACKS AND QUEUES
SUMMARY