The set is the basic structure underlying all of mathematics. In algorithm design, sets are used as the basis of many important abstract data types, and many techniques have been developed for implementing set-based abstract data types. In this chapter we review the basic operations on sets and introduce some simple implementations for sets. We present the "dictionary" and "priority queue," two abstract data types based on the set model. Implementations for these abstract data types are covered in this and the next chapter.
A set is a collection of members (or elements); each member of a set either is itself a set or is a primitive element called an atom. All members of a set are different, which means no set can contain two copies of the same element.
When used as tools in algorithm and data structure design, atoms usually are integers, characters, or strings, and all elements in any one set are usually of the same type. We shall often assume that atoms are linearly ordered by a relation, usually denoted "<" and read "less than" or "precedes." A linear order < on a set S satisfies two properties:
Integers, reals, characters, and character strings have a natural linear ordering for which < is used in Pascal. A linear ordering can be defined on objects that consist of sets of ordered objects. We leave as an exercise how one develops such an ordering. For example, one question to be answered in constructing a linear order for a set of integers is whether the set consisting of integers 1 and 4 should be regarded as being less than or greater than the set consisting of 2 and 3.
A set of atoms is generally exhibited by putting curly brackets around its members, so {1, 4} denotes the set whose only members are 1 and 4. We should bear in mind that a set is not a list, even though we represent sets in this manner as if they were lists. The order in which the elements of a set are listed is irrelevant, and we could just as well have written {4, 1} in place of {1, 4}. Note also that in a set each element appears exactly once, so {1, 4, 1} is not a set.†
Sometimes we represent sets by set formers, which are
expressions of the
form
{
x | statement about x }
where the statement about x is a predicate that tells us exactly what is needed
for an arbitrary object x to be in the set. For example, {x | x is a positive
integer and x ?/FONT> 1000} is another way of representing {1, 2, . .
. , 1000}, and
{x | for some integer y, x = y2} denotes the set of perfect
squares. Note that
the set of perfect squares is infinite and cannot be represented by listing its
members.
The fundamental relationship of set theory is membership, which is denoted by the symbol ?/FONT>. That is, x ?/FONT> A means that element x is a member of set A; the element x could be an atom or another set, but A cannot be an atom. We use x ?/FONT> A for "x is not a member of A." There is a special set, denoted Ø and called the null set or empty set, that has no members. Note that Ø is a set, not an atom, even though the set Ø does not have any members. The distinction is that x ?/FONT> Ø is false for every x, whereas if y is an atom, then x ?/FONT> y doesn't even make sense; it is syntactically meaningless rather than false.
We say set A is included (or contained) in set B, written A ?/FONT> B, or B ?/FONT> A, if every member of A is also a member of B. We also say A is a subset of B and B is a superset of A, if A ?/FONT> B. For example, {1, 2} ?/FONT> {1, 2, 3}, but {1, 2, 3} is not a subset of {1, 2} since 3 is a member of the former but not the latter. Every set is included in itself, and the empty set is included in every set. Two sets are equal if each is included in the other, that is, if their members are the same. Set A is a proper subset or proper superset of set B if A ?/FONT> B, and A ?/FONT> B or A ?/FONT> B, respectively.
The most basic operations on sets are union, intersection, and difference. If A and B are sets, then A ?/FONT> B, the union of A and B, is the set of elements that are members of A or B or both. The intersection of A and B, written A ?/FONT> B, is the set of elements in both A and B, and the difference, A - B, is the set of elements in A that are not in B. For example, if A = {a, b, c} and B = {b, d}, then A ?/FONT> B = {a, b, c, d}, A ?/FONT> B = {b}, and A - B = {a, c}.
We shall consider ADT's that incorporate a variety of set operations. Some collections of these operations have been given special names and have special implementations of high efficiency. Some of the more common set operations are the following.
We begin by defining an ADT for the mathematical model "set" with the three basic set-theoretic operations, union, intersection, and difference. First we give an example where such an ADT is useful and then we discuss several simple implementations of this ADT.
Example 4.1. Let us write a program to do a simple form of "data-flow analysis" on flowcharts that represent procedures. The program will use variables of an abstract data type SET, whose operations are UNION, INTERSECTION, DIFFERENCE, EQUAL, ASSIGN, and MAKENULL, as defined in the previous section.
In Fig. 4.1 we see a flowchart whose boxes have been named B1, . . . , B8, and for which the data definitions (read and assignment statements) have been numbered 1, 2, . . . , 9. This flowchart happens to implement the Euclidean algorithm, to compute the greatest common divisor of inputs p and q, but the details of the algorithm are not relevant to the example.
In general, data-flow analysis refers to that part of a compiler that examines a flowchart-like representation of a source program, such as Fig. 4.1, and collects information about what can be true as control reaches each box of the flowchart. The boxes are often called blocks or basic blocks, and they represent collections of statements through which the flow-of-control proceeds sequentially. The information collected during data-flow analysis is used to help improve the code generated by the compiler. For example, if data-flow analysis told us that each time control reached block B, variable x had the value 27, then we could substitute 27 for all uses of x in block B, unless x were assigned a new value within block B. If constants can be accessed more quickly than variables, this change could speed up the code produced by the compiler.
In our example, we want to determine where a variable could last have been given a new value. That is, we want to compute for each block Bi the set DEFIN[i] of data definitions d such that there is a path from B1 to Bi in which d appears, but is not followed by any other definition of the same variable as d defines. DEFIN[i] is called the set of reaching definitions for Bi.
To see how such information could be useful, consider Fig. 4.1. The first block B1 is a "dummy" block of three data definitions, making the three variables t, p, and q have "undefined" values. If we discover, for example, that DEFIN[7] includes definition 3, which gives q an undefined value, then the program might contain a bug, as apparently it could print q without first assigning a valid value to q. Fortunately, we shall discover that it is impossible to reach block B7 without assigning to q; that is, 3 is not in DEFIN[7].
The computation of the DEFIN[i]'s is aided by several rules. First, we precompute for each block i two sets GEN[i] and KILL[i]. GEN[i] is the set of data definitions in block i, with the exception that if Bi contains two or more definitions of variable x, then only the last is in GEN[i]. Thus, GEN[i] is the set of definitions in Bi that are "generated" by Bi; they reach the end of Bi without having their variables redefined.
The set KILL[i] is the set of definitions d not in Bi such that Bi has a definition of the same variable as d. For example, in Fig. 4.1, GEN[4] = {6}, since definition 6 (of variable t) is in B4 and there are no subsequent definitions of t in B4. KILL[4] = {l, 9}, since these are the definitions of variable t that are not in B4.
Fig. 4.1. A flowchart of the Euclidean algorithm.
In addition to the DEFIN[i]'s, we compute the set DEFOUT[i] for each block Bi. Just as DEFIN[i] is the set of definitions that reach the beginning of Bi, DEFOUT[i] is the set of definitions reaching the end of Bi. There is a simple formula relating DEFIN and DEFOUT, namely
That is, definition d reaches the end of Bi if and only if it either reaches the beginning of Bi and is not killed by Bi, or it is generated in Bi. The second rule relating DEFIN and DEFOUT is that DEFIN[i] is the union, over all predecessors p of Bi, of DEFOUT[p], that is:
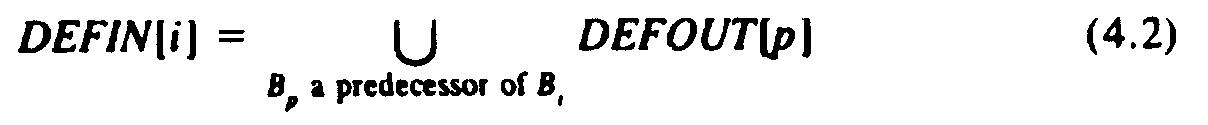
Rule (4.2) says that a data definition enters Bi if and only if it reaches the end of one of Bi's predecessors. As a special case, if Bi has no predecessors, as B1 in Fig. 4.1, then DEFIN[i] = ?/FONT>.
Because we have introduced a variety of new concepts in this example, we shall not try to complicate matters by writing a general algorithm for computing the reaching definitions of an arbitrary flowgraph. Rather, we shall write a part of a program that assumes GEN[i] and KILL[i] are available for i = 1, . . . , 8 and computes DEFIN[i] and DEFOUT[i] for 1, . . . , 8, assuming the particular flowgraph of Fig. 4.1. This program fragment assumes the existence of an ADT SET with operations UNION, INTERSECTION, DIFFERENCE, EQUAL, ASSIGN, and MAKENULL; we shall give alternative implementations of this ADT later.
The procedure propagate( GEN, KILL, DEFIN, DEFOUT) applies rule (4.1) to compute DEFOUT for a block, given DEFIN. If a program were loop-free, then the calculation of DEFOUT would be straightforward. The presence of a loop in the program fragment of Fig. 4.2 necessitates an iterative procedure. We approximate DEFIN[i] by starting with DEFIN[i] = Ø and DEFOUT[i] = GEN[i] for all i, and then repeatedly apply (4.1) and (4.2) until no more changes to DEFIN's and DEFOUT's occur. Since each new value assigned to DEFIN[i] or DEFOUT[i] can be shown to be a superset (not necessarily proper) of its former value, and there are only a finite number of data definitions in any program, the process must converge eventually to a solution to (4.1) and (4.2).
The successive values of DEFIN[i] after each iteration of the repeat-loop are shown in Fig. 4.3. Note that none of the dummy assignments 1, 2, and 3 reaches a block where their variable is used, so there are no undefined variable uses in the program of Fig. 4.1. Also note that by deferring the application of (4.2) for Bi until just before we apply (4.1) for Bi would make the process of Fig. 4.2 converge in fewer iterations in general.
The best implementation of a SET ADT depends on the operations to be performed and on the size of the set. When all sets in our domain of discourse are subsets of a small "universal set" whose elements are the integers 1, . . . , N for some fixed N, then we can use a bit-vector (boolean array) implementation. A set is represented by a bit vector in which the ith bit is true if i is an element of the set. The major advantage of this representation
var
GEN, KILL, DEFIN, DEFOUT: array[l..8] of SET;
{ we assume GEN and KILL are computed externally }
i: integer;
changed: boolean;
procedure propagate ( G, K, I: SET; var
O: SET );
{ apply (4.1) and set changed to true if
a change in DEFOUT is detected }
var
TEMP: SET;
begin
DIFFERENCE(I, K, TEMP);
UNION(TEMP, G, TEMP);
if not EQUAL(TEMP, O) do begin
ASSIGN(O, TEMP);
changed := true
end
end; { propagate }
begin
for i:= 1 to 8 do
ASSIGN(DEFOUT[i], GEN[i]);
repeat
changed := false;
{the next 8 statements apply (4.2) for the
graph of Fig. 4.1 only}
MAKENULL(DEFIN[1]);
ASSIGN(DEFIN[2], DEFOUT[1]);
ASSIGN(DEFIN[3], DEFOUT[2]);
ASSIGN(DEFIN[4], DEFOUT[3]);
UNION(DEFOUT[4], DEFOUT[8], DEFIN[5]);
UNION(DEFOUT[3], DEFOUT[5], DEFIN[6]);
ASSIGN(DEFIN[7], DEFOUT[6]);
ASSIGN(DEFIN[8], DEFOUT[6]);
for i:= 1 to 8 do
propagate(GEN[i], KILL[i],
DEFIN[i], DEFOUT[i]);
until
not changed
end.
Fig. 4.2. Program to compute reaching definitions.
Fig. 4.3. DEFIN[i] after each iteration.
is that MEMBER, INSERT, and DELETE operations can be performed in constant time by directly addressing the appropriate bit. UNION, INTERSECTION, and DIFFERENCE can be performed in time proportional to the size of the universal set.
If the universal set is sufficiently small so that a bit vector fits in one computer word, then UNION, INTERSECTION, and DIFFERENCE can be performed by single logical operations in the language of the underlying machine. Certain small sets can be represented directly in Pascal using the set construct. The maximum size of such sets depends on the particular compiler used and, unfortunately, it is often too small to be used in typical set problems. However, in writing our own programs, we need not be constrained by any limit on our set size, as long as we can treat our sets as subsets of some universal set {1, . . . , N}. We intend that if A is a set represented as a boolean array, then A[i] is true if and only if element i is a member of A. Thus, we can define an ADT SET by the Pascal declaration
const
N = { whatever value is appropriate };
type
SET = packed array[1..N] of boolean;
We can then implement the procedure UNION as shown in Fig. 4.4. To implement INTERSECTION and DIFFERENCE, we replace "or" in Fig. 4.4 by "and" and "and not," respectively. The reader can implement the other operations mentioned in Section 4.1 (except MERGE and FIND, which make little sense in this context) as easy exercises.
It is possible to use the bit-vector implementation of sets when the universal set is a finite set other than a set of consecutive integers. Normally, we would then need a way to translate between members of the universal set and the integers 1, . . . , N. Thus, in Example 4.1 we assumed that the data definitions were assigned numbers from 1 to 9. In general, the translations in
procedure UNION ( A, B: SET; var C: SET ); var i: integer; begin for i := 1 to N do C[i] := A[i] or B[i] end
Fig. 4.4. Implementation of UNION.
both directions could be performed by the MAPPING ADT described in Chapter 2. However, the inverse translation from integers to elements of the universal set can be accomplished better using an array A, where A[i] is the element corresponding to integer i.
It should also be evident that sets can be represented by linked lists, where the items in the list are the elements of the set. Unlike the bit-vector representation, the list representation uses space proportional to the size of the set represented, not the size of the universal set. Moreover, the list representation is somewhat more general since it can handle sets that need not be subsets of some finite universal set.
When we have operations like INTERSECTION on sets represented by linked lists, we have several options. If the universal set is linearly ordered, then we can represent a set by a sorted list. That is, we assume all set members are comparable by a relation "<" and the members of a set appear on a list in the order e1, e2, . . . , en, where e1 < e2 < e3 < . . . < en. The advantage of a sorted list is that we do not need to search the entire list to determine whether an element is on the list.
An element is in the intersection of lists L1 and L2 if and only if it is on both lists. With unsorted lists we must match each element on L1 with each element on L2, a process that takes O(n2) steps on lists of length n. The reason that sorting the lists makes intersection and some other operations easy is that if we wish to match an element e on one list L1 with the elements of another list L2, we have only to look down L2 until we either find e, or find an element greater than e; in the first case we have found the match, while in the second case, we know none exists. More importantly, if d is the element on L1 that immediately precedes e, and we have found onL2 the first element, say f, such that d ?/FONT> f, then to search L2 for an occurrence of e we can begin with f. The conclusion from this reasoning is that we can find matches for all the elements of L1, if they exist, by scanning L1 and L2 once, provided we advance the position markers for the two lists in the proper order, always advancing the one with the smaller element. The routine to implement INTERSECTION is shown in Fig. 4.5. There, sets are represented by linked lists of "cells" whose type is defined
type celltype = record element: elementtype; next: ?/FONT> celltype end
Figure 4.5 assumes elementtype is a type, such as integer, that can be compared by <. If not, we have to write a function that determines which of two elements precedes the other.
The linked lists in Fig. 4.5 are headed by empty cells that serve as entry points to the lists. The reader may, as an exercise, write this program in a more general abstract form using list primitives. The program in Fig. 4.5, however, may be more efficient than the more abstract program. For example, Fig. 4.5 uses pointers to particular cells rather than "position" variables that point to previous cells. We can do so because we only append to list C, and A and B are only scanned, with no insertions or deletions done on those lists.
The operations of UNION and DIFFERENCE can be written to look surprisingly like the INTERSECTION procedure of Fig. 4.5. For UNION, we must attach all elements from either the A or B list to the C list, in their proper, sorted order, so when the elements are unequal (lines 12-14), we add the smaller to the C list just as we do when the elements are equal. We also append to list C all elements on the list not exhausted when the test of line (5) fails. For DIFFERENCE we do not add an element to the C list when equal elements are found. We only add the current A list element to the C list when it is smaller than the current B list element; for then we know the former cannot be found on the B list. Also, we add to C those elements on A when and if the test of line (5) fails because B is exhausted.
The operator ASSIGN(A, B) copies list A into list B. Note that, this operator cannot be implemented simply by making the header cell of A point to the same place as the header cell of B, because in that case, subsequent changes to B would cause unexpected changes to A. The MIN operator is especially easy; just return the first element on the list. DELETE and FIND can be implemented by finding the target item as discussed for general lists and in the case of a DELETE, disposing of its cell.
Lastly, insertion is not difficult to implement, but we must arrange to insert the new element into the proper position. Figure 4.6 shows a procedure INSERT that takes as parameters an element and a pointer to the header cell of a list, and inserts the element into the list. Figure 4.7 shows the crucial cells and pointers just before (solid) and after (dashed) insertion.
procedure INTERSECTION ( ahead, bhead: ?/FONT> celltype;
var pc: ?/FONT> celltype );
{ computes the intersection of sorted lists A and B with
header cells ahead and bhead, leaving the result
as a sorted list whose header is pointed to by pc }
var
acurrent, bcurrent, ccurrent: ?/FONT> celltype;
{the current cells of lists A and B, and the last cell added list C }
begin
(1) new(pc); { create header for list C }
(2) acurrent := ahead?/FONT>.next;
(3) bcurrent := bhead ?/FONT>.next;
(4) ccurrent := pc;
(5) while (acurrent <> nil) and (bcurrent <> nil)
do begin
{ compare current elements on lists A and B }
(6) if acurrent ?/FONT>.element =
bcurrent ?/FONT>.element then begin
{ add to intersection }
(7) new( ccurrent ?/FONT>.next );
(8) ccurrent := ccurrent ?/FONT>.next;
(9) ccurrent ?/FONT>.element := acurrent
?/FONT>.element;
(10 acurrent := acurrent?/FONT>.next;
(11 bcurrent := bcurrent?/FONT>.next
end
else { elements unequal }
(12) if acurrent?/FONT>.element <
bcurrent?/FONT>.element then
(13) acurrent := acurrent?/FONT>.next
else
(14) bcurrent := bcurrent?/FONT>.next
end;
(15) ccurrent?/FONT>.next := nil
end; { INTERSECTION }
Fig. 4.5. Intersection procedure using sorted lists.
When we use a set in the design of an algorithm, we may not need powerful operations like union and intersection. Often, we only need to keep a set of "current" objects, with periodic insertions and deletions from the set. Also, from time to time we may need to know whether a particular element is in the set. A set ADT with the operations INSERT, DELETE, and MEMBER has been given the name dictionary. We shall also include MAKENULL as a dictionary operation to initialize whatever data structure is used in the implementation. Let us consider an example application of the dictionary, and then discuss implementations that are well suited for representing dictionaries.
procedure INSERT ( x: elementtype; p: ?/FONT> celltype );
{ inserts x onto list whose header is pointed to by p }
var
current, newcell: ?/FONT> celltype;
begin
current := p;
while current?/FONT>.next <>
nil do begin
if current?/FONT>.next?/FONT>.element = x then
return; { if x is already on the list, return }
if current?/FONT>.next?/FONT>.element > x then
goto add; { break }
current: = current?/FONT>.next
end;
add: { current is now the cell after which x is to be inserted }
new(newcell);
newcell?/FONT>.element := x;
newcell?/FONT>.next :=
current?/FONT>.next;
current?/FONT>.next := newcell
end; { INSERT }
Fig. 4.6. Insertion procedure.
Example 4.2. The Society for the Prevention of Injustice to Tuna (SPIT) keeps a database recording the most recent votes of legislators on issues of importance to tuna lovers. This database is, conceptually, two sets of legislators' names, called goodguys and badguys. The society is very forgiving of past mistakes, but also tends to forget former friends easily. For example, if a vote to declare Lake Erie off limits to tuna fishermen is taken, all legislators voting in favor will be inserted into goodguys and deleted from badguys, while the opposite will happen to those voting against. Legislators not voting remain in whatever set they were in, if any.
In operation, the database system accepts three commands, each represented by a single character, followed by a ten character string denoting the name of a legislator. Each command is on a separate line. The commands are:
We also allow the character 'E' on the input line to signal the end of processing. Figure 4.8 shows the sketch of the program, written in terms of the as-yet-undefined ADT DICTIONARY, which in this case is intended to be a set of strings of length 10.
Fig. 4.7. The insertion picture.
A dictionary can be implemented by a sorted or unsorted linked list. Another possible implementation of a dictionary is by a bit vector, provided the elements of the underlying set are restricted to the integers 1, . . . , N for some N, or are restricted to a set that can be put in correspondence with such a set of integers.
A third possible implementation of a dictionary is to use a fixed- length array with a pointer to the last entry of the array in use. This implementation is only feasible if we can assume our sets never get larger than the length of the array. It has the advantage of simplicity over the linked-list representation, while its disadvantages are that (1) sets cannot grow arbitrarily, (2 deletion is slower, and (3) space is not utilized efficiently if sets are of varying sizes.
It is for the last of these reasons that we did not discuss the array implementation in connection with sets whose unions and intersections were taken frequently. Since arrays as well as lists can be sorted, however, the reader could consider the array implementation we now describe for dictionaries as a possible implementation for sets in general. Figure 4.9 shows the declarations and procedures necessary to supplement Fig. 4.8 to make it a working program.
program tuna ( input, output );
{ legislative database }
type
nametype = array[l..10] of char;
var
command: char;
legislator: nametype;
goodguys, badguys: DICTIONARY;
procedure favor (friend: nametype );
begin
INSERT(friend, goodguys) ;
DELETE(friend, badguys)
end; { favor }
procedure unfavor ( foe: nametype );
begin
INSERT(foe, badguys ) ;
DELETE(foe, goodguys )
end; { unfavor }
procedure report ( subject: nametype );
begin
if MEMBER(subject, goodguys) then
writeln(subject, 'is a friend')
else if MEMBER(subject, badguys) then
writeln(subject, 'is a foe')
else
writeln('we have no information about ', subject)
end; { report }
begin { main program }
MAKENULL(goodguys);
MAKENULL(badguys);
read(command);
while command < > 'E' do begin
readln (legislator);
if command = 'F' then
favor(legislator)
else if command = 'U' then
unfavor(legislator)
else if command = '?' then
report(legislator)
else
error('unknown command');
read(command)
end
end. { tuna }
Fig. 4.8. Outline of the SPIT database program.
const
maxsize = { some suitable number };
type
DICTIONARY = record
last: integer;
data: array[l..maxsize] of nametype
end;
procedure MAKENULL ( var A: DICTIONARY );
begin
A.last := 0
end; { MAKENULL }
function MEMBER ( x: nametype; var A: DICTIONARY ):
boolean;
var
i: integer;
begin
for i := 1 to A.last do
if A.data [i] = x then return (true);
return (false) { if x is not found }
end; { MEMBER }
procedure INSERT ( x: nametype; var A: DICTIONARY );
begin
if not MEMBER(x, A ) then
If A.last < maxsize then begin
A.last := A.last + 1;
A.data[A.last ] := x
end
else error ('database is full')
end; { INSERT }
procedure DELETE ( x: nametype; var A: DICTIONARY );
var
i: integer;
begin
if A.last > 0 then begin
i := 1;
while (A.data[i] <> x) and (i <
A.last) do
i := i + 1;
{ when we reach here, either x has been found, or
we are at the last element in set A, or both }
if A.data[i] = x then begin
A.data[i] := A.data[A.last];
{ move the last element into the place of x;
Note that if i = A.last, this step does
nothing, but the next step will delete x }
A.last := A.last - 1
end
end
end; { DELETE }
Fig. 4.9. Type and procedure declarations for array dictionary.
The array implementation of dictionaries requires, on the average, O(N) steps to execute a single INSERT, DELETE, or MEMBER instruction on a dictionary of N elements; we get a similar speed if a list implementation is used. The bit-vector implementation takes constant time to do any of these three operations, but we are limited to sets of integers in some small range for that implementation to be feasible.
There is another important and widely useful technique for implementing dictionaries called "hashing." Hashing requires constant time per operation, on the average, and there is no requirement that sets be subsets of any particular finite universal set. In the worst case, this method requires time proportional to the size of the set for each operation, just as the array and list implementations do. By careful design, however, we can make the probability of hashing requiring more than a constant time per operation be arbitrarily small.
We shall consider two somewhat different forms of hashing. One, called open or external hashing, allows the set to be stored in a potentially unlimited space, and therefore places no limit on the size of the set. The second, called closed or internal hashing, uses a fixed space for storage and thus limits the size of sets.†
In Fig. 4.10 we see the basic data structure for open hashing. The essential idea is that the (possibly infinite) set of potential set members is partitioned into a finite number of classes. If we wish to have B classes, numbered 0, 1, . . . , B-1, then we use a hash function h such that for each object x of the data type for members of the set being represented, h(x) is one of the integers 0 through B-1. The value of h(x), naturally, is the class to which x belongs. We often call x the key and h(x) the hash value of x. The "classes" we shall refer to as buckets, and we say that x belongs to bucket h(x).
In an array called the bucket table, indexed by the bucket numbers 0, 1, . . . , B-1, we have headers for B lists. The elements on the ith list are the members of the set being represented that belong to class i, that is, the elements x in the set such that h(x) = i.
It is our hope that the buckets will be roughly equal in size, so the list for each bucket will be short. If there are N elements in the set, then the average bucket will have N/B members. If we can estimate N and choose B to be roughly as large, then the average bucket will have only one or two members, and the dictionary operations take, on the average, some small constant number of steps, independent of what N (or equivalently B) is.
Fig. 4.10. The open hashing data organization.
It is not always clear that we can select h so that a typical set will have its members distributed fairly evenly among the buckets. We shall later have more to say about selecting h so that it truly "hashes" its argument, that is, so that h(x) is a "random" value that is not dependent on x in any trivial way.
function h ( x: nametype ) : O..B - 1;
var
i, sum: integer
begin
sum: = 0;
for i: 1 to 10 do
sum: = sum + ord(x[i]);
h : = sum + ord(x[i]);
end { h }
Fig. 4.11. A simple hash function h.
Let us here, for specificity, introduce one hash function on character strings that is fairly good, although not perfect. The idea is to treat the characters as integers, using the character code of the machine to define the correspondence. Pascal provides the ord built-in function, where ord(c) is the integer code for character c. Thus, if x is a key and the type of keys is array[l..10] of char (what we called nametype in Example 4.2), we might declare the hash function h as in Fig. 4.11. In that function we sum the integers for each character and divide the result by B, taking the remainder, which is an integer from 0 to B - 1.
In Fig. 4.12 we see the declarations of the data structures for an open hash table and the procedures implementing the operations for a dictionary. The member type for the dictionary is assumed to be nametype (a character array), so these declarations can be used in Example 4.2 directly. We should note that in Fig. 4.12 we have made the headers of the bucket lists be pointers to cells, rather than complete cells. We did so because the bucket table, where the headers are, could take as much space as the lists themselves if we made the bucket be an array of cells rather than pointers. Notice, however, that we pay a price for saving this space. The code for the DELETE procedure now must distinguish the first cell from the remaining ones.
const
B = { suitable constant };
type
celltype = record
element: nametype;
next: ?/FONT> celltype
end;
DICTIONARY = array[0..B - l] of ?/FONT> celltype;
procedure MAKENULL ( var A: DICTIONARY );
var
i: integer;
begin
for i:= 0 to B-1 do
A [i]:= nil
end; { MAKENULL }
function MEMBER ( x: nametype; var A: DICTIONARY ) : boolean;
var
current: ?/FONT> celltype;
begin
current := A [h (x)];
{ initially current is the header of x's bucket }
while current < > nil do
if current?/FONT>.element =
x then
return (true)
else
current := current?/FONT>.next;
return (false) { if x is not found }
end; { MEMBER }
procedure INSERT ( x: nametype; var A: DICTIONARY );
var
bucket: integer;
oldheader: ?/FONT> celltype;
begin
if not MEMBER(x, A) then begin
bucket := h(x);
oldheader := A [bucket ];
new (A [bucket]);
A [bucket ]?/FONT>.element :=
x;
A [bucket ]?/FONT>.next: =
oldheader
end
end; { INSERT }
procedure DELETE ( x: nametype; var A: DICTIONARY );
var
current: ?/FONT> celltype;
bucket: integer;
begin
bucket := h(x);
if A [bucket ] < > nil then begin
if A [bucket]?/FONT>.element
= x then { x is in first cell }
A [bucket ] := A [bucket ]?/FONT>.next { remove x from list }
else begin { x, if present at all, is not in first cell of bucket }
current := A [bucket ]; { current points to the previous
cell }
while current?/FONT>.next <> nil
do
if current?/FONT>.next?/FONT>.element = x then begin
current?/FONT>.next :=
current?/FONT>.next?/FONT>.next;
{ remove x from list }
return { break }
end
else {x not yet found}
current := current?/FONT>.next
end
end
end; { DELETE }
Fig. 4.12. Dictionary implementation by an open hash table.
A closed hash table keeps the members of the dictionary in the bucket table itself, rather than using that table to store list headers. As a consequence, it appears that we can put only one element in any bucket. However, associated with closed hashing is a rehash strategy. If we try to place x in bucket h(x) and find it already holds an element, a situation called a collision occurs, and the rehash strategy chooses a sequence of alternative locations, h1(x), h2(x), . . . , within the bucket table in which we could place x. We try each of these locations, in order, until we find an empty one. If none is empty, then the table is full, and we cannot insert x.
Example 4.3. Suppose B = 8 and keys a, b, c, and d have hash values h(a) = 3, h(b) = 0, h(c) = 4, h(d) = 3. We shall use the simplest rehash strategy, called linear hashing, where hi(x) = (h(x) + i) mod B. Thus, for example, if we wished to insert a and found bucket 3 already filled, we would try buckets 4, 5, 6, 7, 0, 1, and 2, in that order.
Initially, we assume the table is empty, that is, each bucket holds a special value empty, which is not equal to any value we might try to insert.† If we insert a, b, c, and d, in that order, into an initially empty table, we find a goes into bucket 3, b into 0 and c into 4. When we try to insert d, we first try h(d) = 3 and find it filled. Then we try h1(d) = 4 and find it filled as well. Finally, when we try h2(d) = 5, we find an empty space and put d there. The resulting positions are shown in Fig. 4.13.
Fig. 4.13. Partially filled hash table.
The membership test for an element x requires that we examine h(x), hi(x), h2(x), . . . , until we either find x or find an empty bucket. To see why we can stop looking if we reach an empty bucket, suppose first that there are no deletions permitted. If, say, h3(x) is the first empty bucket found in the series, it is not possible that x is in bucket h4(x), h5(x), or further along the sequence, because x could not have been placed there unless h3(x) were filled at the time we inserted x.
Note, however, that if we allow deletions, then we can never be sure, if we reach an empty bucket without finding x, that x is not somewhere else, and the now empty bucket was occupied when x was inserted. When we must do deletions, the most effective approach is to place a constant called deleted into a bucket that holds an element that we wish to delete. It is important that we can distinguish between deleted and empty, the constant found in all buckets that have never been filled. In this way it is possible to permit deletions without having to search the entire table during a MEMBER test. When inserting we can treat deleted as an available space, so with luck the space of a deleted element will eventually be reused. However, as the space of a deleted element is not immediately reclaimable as it is with open hashing, we may prefer the open to the closed scheme.
Example 4.4. Suppose we wish to test if e is in the set represented by Fig. 4.13. If h(e) = 4, we try buckets 4, 5, and then 6. Bucket 6 is empty and since we have not found e, we conclude e is not in the set.
If we delete c, we must put the constant deleted in bucket 4. In that way, when we look for d, and we begin at h(d) = 3, we shall scan 4 and 5 to find d, and not stop at 4 as we would if we put empty in that bucket.
In Fig 4.14 we see the type declarations and operations for the DICTIONARY ADT with set members of type nametype and the closed hash table as the underlying implementation. We use an arbitrary hash function h, of which Fig. 4.11 is one possibility, and we use the linear hashing strategy to rehash in case of collisions. For convenience, we have identified empty with a string of ten blanks and deleted with a string of 10 *'s, assuming that neither of these strings could be real keys. (In the SPIT database these strings are unlikely to be names of legislators.) The procedure INSERT(x, A ) first uses locate to determine if x is already in A, and, if not, it uses a special routine locate 1 to find a location in which to insert x. Note that locate 1 searches for deleted as well as empty locations.
const
empty = ' '; { 10 blanks }
deleted = '**********'{ 10 *'s }
type
DICTIONARY = array[0..B -1] of nametype;
procedure MAKENULL ( var A: DICTIONARY );
var
i: integer;
begin
for i := 0 to B - 1 do
A [i] := empty
end; {MAKENULL}
function locate ( x: nametype; A: DICTIONARY ) : integer;
{ locate scans DICTIONARY from the bucket for h(x) until
either x is found, or an empty bucket is found, or it has
scanned completely around the table, thereby determining
that the table does not contain x. locate returns the index
of the bucket at which it stops for any of these reasons }
var
initial, i: integer;
{ initial holds h(x); i counts the number of
buckets thus far scanned when looking for x }
begin
initial := h(x);
i := 0;
while (i < B) and (A [(initial +
i) mod B ] <> x) and
(A [(initial + i) mod B] <>
empty) do
i := i + 1;
return ((initial + i) mod B)
end; { locate }
function locate 1 ( x: nametype; A: DICTIONARY ) : integer;
{ like locate, but it will also stop at and return a deleted entry }
function MEMBER ( x: nametype; var A: DICTIONARY ) :
boolean;
begin
if A [locate(x)] = x then
return (true)
else
return (false)
end; { MEMBER }
procedure INSERT (x: nametype; var A: DICTIONARY );
var
bucket: integer;
begin
if A[locate (x)] = x then return; { x
is already in A }
bucket := locate 1(x);
if (A [bucket] = empty) or (A
[bucket] = deleted) then
A [bucket] := x
else
error('INSERT failed: table is full')
end; { INSERT }
procedure DELETE ( x: nametype; var A: DICTIONARY );
var
bucket: integer;
begin
bucket := locate(x);
if A [bucket] = x then
A [bucket] := deleted
end; { DELETE }
Fig. 4.14. Dictionary implementation by a closed hash table.
As we have mentioned, hashing is an efficient way to represent dictionaries and some other abstract data types based on sets. In this section we shall examine the average time per dictionary operation in an open hash table. If there are B buckets and N elements stored in the hash table, then the average bucket has N/B members, and we expect that an average INSERT, DELETE, or MEMBER operation will take O(1 + N/B) time. The constant 1 represents the time to find the bucket, and N/B the time to search the bucket. If we can choose B to be about N, this time becomes a constant per operation. Thus the average time to insert, delete, or test an element for membership, assuming the element is equally likely to be hashed to any bucket, is a constant independent of N.
Suppose we are given a program written in some language like Pascal, and we wish to insert all identifiers appearing in the program into a hash table. Whenever a declaration of a new identifier is encountered, the identifier is inserted into the hash table after checking that it is not already there. During this phase it is reasonable to assume that an identifier is equally likely to be hashed into any given bucket. Thus we can construct a hash table with N elements in time O(N(1 + N/B)). By choosing B equal to N this becomes O(N).
In the next phase identifiers are encountered in the body of the program. We must locate the identifiers in the hash table to retrieve information associated with them. But what is the expected time to locate an identifier? If the element searched for is equally likely to be any element in the table, then the expected time to search for it is just the average time spent inserting an element. To see this, observe that in searching once for each element in the table, the time spent is exactly the same as the time spent inserting each element, assuming that elements are always appended to the end of the list for the appropriate bucket. Thus the expected time for a search is also 0(1 + N/B).
The above analysis assumes that a hash function distributes elements uniformly over the buckets. Do such functions exist? We can regard a function such as that of Fig. 4.11 (convert characters to integers, sum and take the remainder modulo B) as a typical hash function. The following example examines the performance of this hash function.
Example 4.5. Suppose we use the hash function of Fig. 4.11 to hash the 100 keys consisting of the character strings A0, A1, . . . , A99 into a table of 100 buckets. On the assumption that ord(O), ord(1), . . . , ord(9) form an arithmetic progression, as they do in the common character codes ASCII and EBCDIC, it is easy to check that the keys hash into at most 29 of the 100 buckets,† and the largest bucket contains A18, A27, A36, . . . , A90, or 9 of the 100 elements. If we compute the average number of steps for insertion, using the fact that the insertion of the ith element into a bucket takes i + 1 steps, we get 395 steps for these 100 keys. In comparison, our estimate N(1 + N/B) would suggest 200 steps.
The simple hashing function of Fig. 4.11 may treat certain sets of inputs, such as the consecutive strings in Example 4.5, in a nonrandom manner. "More random" hash functions are available. As an example, we can use the idea of squaring and taking middle digits. Thus, if we have a 5-digit number n as a key and square it, we get a 9 or 10 digit number. The "middle digits," such as the 4th through 7th places from the right, have values that depend on almost all the digits of n. For example, digit 4 depends on all but the leftmost digit of n, and digit 5 depends on all digits of n. Thus, if B = 100, we might choose to take digits 6 and 5 to form the bucket number.
This idea can be generalized to situations where B is not a power of 10. Suppose keys are integers in the range 0, 1, . . . , K. If we pick an integer C such that BC2 is about equal to K2, then the function
h(n) = [n2/C] mod B
effectively extracts a base-B digit from the middle of n2.
Example 4.6. If K = 1000 and B = 8, we might choose C = 354. Then
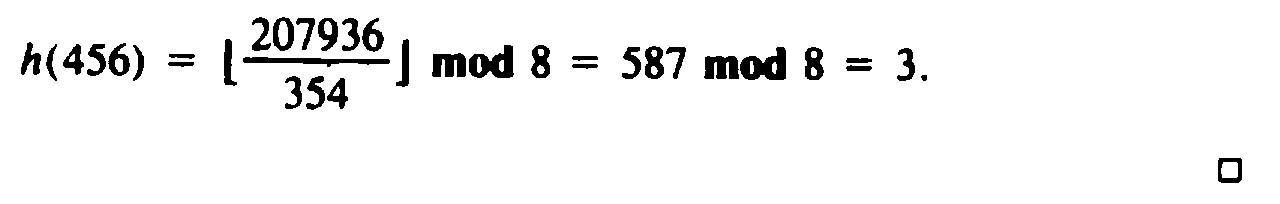
To use the "square and take the middle" strategy when keys are character strings, first group the characters in the string from the right into blocks of a fixed number of characters, say 4, padding the left with blanks, if necessary. Treat each block as a single integer, formed by concatenating the binary codes for the characters. For example, ASCII uses a 7-bit character code, so characters may be viewed as "digits" in base 27, or 128. Thus we can regard the character string abcd as the integer (128)3a + (128)2b + (128)c + d. After converting all blocks to integers, add them† and proceed as we have suggested previously for integers.
In a closed hashing scheme the speed of insertion and other operations depends not only on how randomly the hash function distributes the elements into buckets, but also on how well the rehashing strategy avoids additional collisions when a bucket is already filled. For example, the linear strategy for resolving collisions is not as good as possible. While the analysis is beyond the scope of this book, we can observe the following. As soon as a few consecutive buckets are filled, any key that hashes to one of them will be sent, by the rehash strategy, to the end of the group, thereby increasing the length of that consecutive group. We are thus likely to find more long runs of consecutive buckets that are filled than if elements filled buckets at random. Moreover, runs of filled blocks cause some long sequences of tries before a newly inserted element finds an empty bucket, so having unusually large runs of filled buckets slows down insertion and other operations.
We might wish to know how many tries (or probes) are necessary on the average to insert an element when N out of B buckets are filled, assuming all combinations of N out of B buckets are equally likely to be filled. It is generally assumed, although not proved, that no closed hashing strategy can give a better average time performance than this for the dictionary operations. We shall then derive a formula for the cost of insertion if the alternative locations used by the rehashing strategy are chosen at random. Finally, we shall consider some strategies for rehashing that approximate random behavior.
The probability of a collision on our initial probe is N/B.
Assuming a collision, our first rehash will try one of B - 1 buckets, of which N - 1 are
filled, so the probability of at least two collisions is
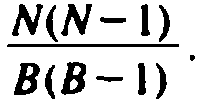Similarly, the
probability of at least i collisions is
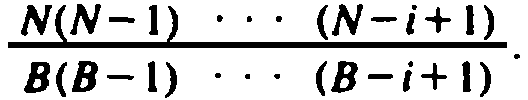
If B and N are large, this probability approximates (N/B)i.
The average
number of probes is one (for the successful insertion) plus the sum over all
i ?/FONT> 1 of the probability of at least i collisions, that is,
approximately
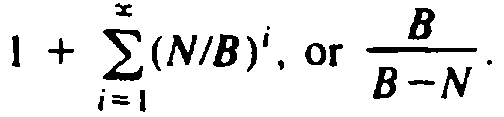. It can be shown that the exact value of
the summation when formula (4.3) is substituted for (N/B)i is
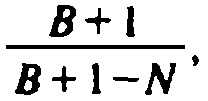, so our
approximation is a good one except when N is very close to B.
Observe that
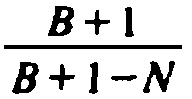grows very slowly as N begins to grow from 0 to
B - 1, the largest value of N for which another insertion is possible. For
example, if N is half B, then about two probes are needed for the next
insertion, on the average. The average insertion cost per bucket to fill M of the B
buckets is
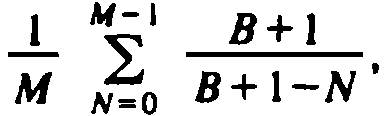, which is approximately 
, or
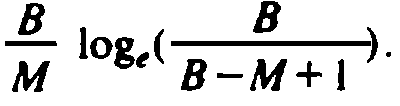Thus, to fill the table completely
(M = B) requires an
average of logeB per bucket, or B logeB probes in
total. However, to fill the
table to 90% of capacity (M = .9B) only requires B((10/9) logel0)
or
approximately 2.56B probes.
The average cost of the membership test for a nonexistent element is the same as the cost of inserting the next element, but the cost of the membership test for an element in the set is the average cost of all insertions made so far, which is substantially less if the table is fairly full. Deletions have the same average cost as membership testing. But unlike open hashing, deletions from a closed hash table do not help speed up subsequent insertions or membership tests. It should be emphasized that if we never fill closed hash tables to more than any fixed fraction less than one, the average cost of operations is a constant; the constant grows as the permitted fraction of capacity grows. Figure 4.15 graphs the cost of insertions, deletions and membership tests, as a function of the percentage of the table that is full at the time the operation is performed.
Fig. 4.15. Average operation cost.
We have observed that the linear rehashing strategy tends to group full buckets into large consecutive blocks. Perhaps we could get more "random" behavior if we probed at a constant interval greater than one. That is, let hi(x) = (h(x)+ci) mod B for some c > 1. For example, if B = 8, c = 3, and h(x) = 4, we would probe buckets 4, 7, 2, 5, 0, 3, 6, and 1, in that order. Of course, if c and B have a common factor greater than one, this strategy doesn't even allow us to search all buckets; try B = 8 and c = 2, for example. But more significantly, even if c and B are relatively prime (have no common factors), we have the same "bunching up" problem as with linear hashing, although here it is sequences of full buckets separated by difference c that tend to occur. This phenomenon slows down operations as for linear hashing, since an attempted insertion into a full bucket will tend to travel down a chain of full buckets separated by distance c, and the length of this chain will increase by one.
In fact, any rehashing strategy where the target of a probe depends only on the target of the previous probe (as opposed to depending on the number of unsuccessful probes so far, the original bucket h(x), or the value of the key x itself) will exhibit the bunching property of linear hashing. Perhaps the simplest strategy in which the problem does not occur is to let hi(x) = (h(x)+di) mod B where d1, d2, . . . , dB-1 is a "random" permutation of the integers 1, 2, . . . , B-1. Of course, the same sequence d1, . . . , dB-1 is used for all insertions, deletions and membership tests; the "random" shuffle of the integers is decided upon once, when we design the rehash algorithm.
The generation of "random" numbers is a complicated subject, but fortunately, many common methods do produce a sequence of "random" numbers that is actually a permutation of integers from 1 up to some limit. These random number generators, if reset to their initial values for each operation on the hash table, serve to generate the desired sequence d1, . . . , dB-1.
One effective approach uses "shift register sequences." Let B be a power of 2 and k a constant between 1 and B-1. Start with some number d1 in the range 1 to B - 1, and generate successive numbers in the sequence by taking the previous value, doubling it, and if the result exceeds B, subtracting B and taking the bitwise modulo 2 sum of the result and the selected constant k. The bitwise modulo 2 sum of x and y, written x ?/FONT> y, is computed by writing x and y in binary, with leading 0's if necessary so both are of the same length, and forming the numbers whose binary representation has a 1 in those positions where one, but not both, of x and y have a 1.
Example 4.7. 25 ?/FONT> 13 is computed by taking
25 = 11001
13 = 01101
______
25 ?/FONT> 13 = 10100
Note that this "addition" can be thought of as ordinary binary addition with carries from place to place ignored.
Not every value of k will produce a permutation of 1, 2, . . . , B-1; sometimes a number repeats before all are generated. However, for given B, there is a small but finite chance that any particular k will work, and we need only find one k for each B.
Example 4.8. Let B = 8. If we pick k = 3, we succeed in generating all of 1, 2, . . . , 7. For example, if we start with d1 = 5, then we compute d2 by first doubling d1 to get 10. Since 10 > 8, we subtract 8 to get 2, and then compute d2 = 2 ?/FONT> 3 = 1. Note that x ?/FONT> 3 can be computed by complementing the last two bits of x.
It is instructive to see the 3-bit binary representations of d1, d2, . . . , d7. These are shown in Fig. 4.16, along with the method of their calculation. Note that multiplication by 2 corresponds to a shift left in binary. Thus we have a hint of the origin of the term "shift register sequence."
Fig. 4.16. Calculating a shift register sequence.
The reader should check that we also generate a permutation of 1, 2, . . . ,7 if we choose k = 5, but we fail for other values of k.
If we use an open hash table, the average time for operations increases as N/B, a quantity that grows rapidly as the number of elements exceeds the number of buckets. Similarly, for a closed hash table, we saw from Fig. 4.15 that efficiency goes down as N approaches B, and it is not possible that N exceeds B.
To retain the constant time per operation that is theoretically possible with hash tables, we suggest that if N gets too large, for example N ?/FONT> .9B for a closed table or N ?/FONT> 2B for an open one, we simply create a new hash table with twice as many buckets. The insertion of the current members of the set into the new table will, on the average, take less time than it took to insert them into the smaller table, and we more than make up this cost when doing subsequent dictionary operations.
Recall our discussion of the MAPPING ADT from Chapter 2 in which we defined a mapping as a function from domain elements to range elements. The operations for this ADT are:
The hash table is an effective way to implement a mapping. The
operations ASSIGN and COMPUTE are implemented much like INSERT and
MEMBER operations for a dictionary. Let us consider an open hash table
first. We assume the hash function h(d) hashes domain elements to bucket
numbers. While for the dictionary, buckets consisted of a linked list of
elements, for the mapping we need a list of domain elements paired with their
range values. That is, we replace the cell definition in Fig. 4.12 by
type
celltype = record
domainelement: domaintype;
range: rangetype;
next: ?/FONT> celltype
end
where domaintype and rangetype are whatever types domain and range
elements have in this mapping. The declaration of a MAPPING is
type
MAPPING = array[0..B-1] of ?/FONT> celltype
This array is the bucket array for a hash table. The procedure ASSIGN is written in Fig. 4.17. The code for MAKENULL and COMPUTE are left as an exercise.
Similarly, we can use a closed hash table as a mapping. Define cells to consist of domain element and range fields and declare a MAPPING to be an array of cells. As for open hash tables, let the hash function apply to domain elements, not range elements. We leave the implementation of the mapping operations for a closed hash table as an exercise.
The priority queue is an ADT based on the set model with the operations
INSERT and DELETEMIN, as well as the usual MAKENULL for
initialization of the data structure. To define the new operation, DELETEMIN, we
first assume that elements of the set have a "priority" function defined on
procedure ASSIGN ( var A: MAPPING; d: domaintype;
r: rangetype );
var
bucket: integer;
current: ?/FONT> celltype;
begin
bucket := h(d);
current := A[bucket];
while current <> nil do
if current?/FONT>.domainelement = d then begin
current?/FONT>.range := r;
{ replace old value for d }
return
end
else
current := current?/FONT>.next;
{ at this point, d was not found on the list }
current := A[bucket]; { use current to remember first cell
}
new(A[bucket]);
A [bucket]?/FONT>.domainelement
:= d;
A [bucket]?/FONT>.range: =
r;
A [bucket]?/FONT>.next :=
current
end; { ASSIGN }
Fig. 4.17. The procedure ASSIGN for an open hash table.
them; for each element a, p(a), the priority of a, is a real number or, more generally, a member of some linearly ordered set. The operation INSERT has the usual meaning, while DELETEMIN is a function that returns some element of smallest priority and, as a side effect, deletes it from the set. Thus, as its name implies, DELETEMIN is a combination of the operations DELETE and MIN discussed earlier in the chapter.Example 4.9. The term "priority queue" comes from the following sort of use for this ADT. The word "queue" suggests that people or entities are waiting for some service, and the word "priority" suggests that the service is given not on a "first-come-first-served" basis as for the QUEUE ADT, but rather that each person has a priority based on the urgency of need. An example is a hospital waiting room, where patients having potentially fatal problems will be taken before any others, no matter how long the respective waits are.
As a more mundane example of the use of priority queues, a time- shared computing system needs to maintain a set of processes waiting for service. Usually, the system designers want to make short processes appear to be instantaneous (in practice, response within a second or two appears instantaneous), so these are given priority over processes that have already consumed substantial time. A process that requires several seconds of computing time cannot be made to appear instantaneous, so it is sensible strategy to defer these until all processes that have a chance to appear instantaneous have been done. However, if we are not careful, processes that have taken substantially more time than average may never get another time slice and will wait forever.
One possible way to favor short processes, yet not lock out long ones is to give process P a priority 100tused(P) - tinit(P). The parameter tused gives the amount of time consumed by the process so far, and tinit gives the time at which the process initiated, measured from some "time zero." Note that priorities will generally be large negative integers, unless we choose to measure tinit from a time in the future. Also note that 100 in the above formula is a "magic number"; it is selected to be somewhat larger than the largest number of processes we expect to be active at once. The reader may observe that if we always pick the process with the smallest priority number, and there are not too many short processes in the mix, then in the long run, a process that does not finish quickly will receive 1% of the processor's time. If that is too much or too little, another constant can replace 100 in the priority formula.
We shall represent processes by records consisting of a process identifier and a priority number. That is, we define
type
processtype = record
id: integer;
priority: integer
end;
The priority of a process is the value of the priority field, which here we have defined to be an integer. We can define the priority function as follows.
function p (
a: processtype ): integer;
begin
return (a.priority)
end;
In selecting processes to receive a time slice, the system maintains a priority queue WAITING of processtype elements and uses two procedures, initial and select, to manipulate the priority queue by the operations INSERT and DELETEMIN. Whenever a process is initiated, procedure initial is called to place a record for that process in WAITING. Procedure select is called when the system has a time slice to award to some process. The record for the selected process is deleted from WAITING, but retained by select for reentry into the queue with a new priority; the priority is increased by 100 times the amount of time used.
We make use of function currenttime, which returns the current time, in whatever time units are used by the system, say microseconds, and we use procedure execute(P) to cause the process with identifier P to execute for one time slice. Figure 4.18 shows the procedures initial and select.
procedure initial ( P: integer );
{ initial places process with id P on the queue }
var
process: processtype;
begin
process.id := P;
process.priority := - currenttime;
INSERT (process, WAITING)
end; { initial }
procedure select;
{ select allocates a time slice to process with highest priority }
var
begintime, endtime: integer;
process: processtype;
begin
process := ?/FONT> DELETEMIN(WAITING);
{ DELETEMIN returns a pointer to the deleted element }
begintime := currenttime;
execute (process.id);
endtime := currenttime;
process.priority := process.priority + 100*(endtime -
begintime);
{ adjust priority to incorporate amount of time used }
INSERT (process, WAITING)
{ put selected process back on queue with new priority }
end; { select }
Fig. 4.18. Allocating time to processes.
With the exception of the hash table, the set implementations we have studied so far are also appropriate for priority queues. The reason the hash table is inappropriate is that there is no convenient way to find the minimum element, so hashing merely adds complications, and does not improve performance over, say, a linked list.
If we use a linked list, we have a choice of sorting it or leaving it unsorted. If we sort the list, finding a minimum is easy -- just take the first element on the list. However, insertion requires scanning half the list on the average to maintain the sorted list. On the other hand, we could leave the list unsorted, which makes insertion easy and selection of a minimum more difficult.
Example 4.10. We shall implement DELETEMIN for an unsorted list of elements of type processtype, as defined in Example 4.9. The list is headed by an empty cell. The implementations of INSERT and MAKENULL are straightforward, and we leave the implementation using sorted lists as an exercise. Figure 4.19 gives the declaration for cells, for the type PRIORITYQUEUE, and for the procedure DELETEMIN.
Whether we choose sorted or unsorted lists to represent priority queues, we must spend time proportional to n to implement one or the other of INSERT or DELETEMIN on sets of size n. There is another implementation in which DELETEMIN and INSERT each require O(logn) steps, a substantial improvement for large n (say n ?/FONT> 100). The basic idea is to organize the elements of the priority queue in a binary tree that is as balanced as possible; an example is in Fig. 4.20. At the lowest level, where some leaves may be missing, we require that all missing leaves are to the right of all leaves that are present on the lowest level.
Most importantly, the tree is partially ordered, meaning that the priority of node v is no greater than the priority of the children of v, where the priority of a node is the priority number of the element stored at the node. Note from Fig. 4.20 that small priority numbers need not appear at higher levels than larger priority numbers. For example, level three has 6 and 8, which are less than the priority number 9 appearing on level 2. However, the parent of 6 and 8 has priority 5, which is, and must be, at least as small as the priorities of its children.
To execute DELETEMIN, we return the minimum-priority element, which, it is easily seen, must be at the root. However, if we simply remove the root, we no longer have a tree. To maintain the property of being a partially ordered tree, as balanced as possible, with leaves at the lowest level as far left as can be, we take the rightmost leaf at the lowest level and temporarily put it at the root. Figure 4.21(a) shows this change from Fig. 4.20. Then we push this element as far down the tree as it will go, by exchanging it with the one of its children having smaller priority, until the element is either at a leaf or at a position where it has priority no larger than either of its children.
In Fig. 4.21(a) we must exchange the root with its smaller-priority child, which has priority 5. The result is shown in Fig. 4.21(b). The element being pushed down is still larger than its children, with priorities 6 and 8. We exchange it with the smaller of these, 6, to reach the tree of Fig. 4.21(c). This tree has the partially ordered property.
In this percolation, if a node v has an element with
priority a, if its
children have elements with priorities b and c, and if at least one of b and c
is
smaller than a, then exchanging a with the smaller of b and c results in
v
having an element whose priority is smaller than either of its children. To
prove this, suppose b ?/FONT> c. After the exchange, node
v acquires b, and its
type
celltype = record
element: processtype;
next: ?/FONT> celltype
end;
PRIORITYQUEUE = ?/FONT> celltype;
{ cell pointed to is a list header }
function DELETEMIN ( var A: PRIORITYQUEUE ): ?/FONT> celltype;
var
current: ?/FONT> celltype; { cell before one being
"scanned" }
lowpriority: integer; { smallest priority found so far }
prewinner: ?/FONT> celltype; { cell before one with
element
of smallest priority }
begin
if A ?/FONT>.next = nil
then
error('cannot find minimum of empty list')
else begin
lowpriority := p(A?/FONT>.next?/FONT>.element);
{ p returns priority of the first element. Note A points
to a header cell that does not contain an element }
prewinner := A;
current := A?/FONT>.next;
while current?/FONT>.next <>
nil do begin
{ compare priorities of current winner
and next element }
if p( current?/FONT>.next?/FONT>.element) <
lowpriority then begin
prewinner := current;
lowpriority : = p (current?/FONT>.next?/FONT>. element)
end;
current := current?/FONT>.next
end;
DELETEMIN := prewinner?/FONT>.next;
{ return pointer to the winner }
prewinner?/FONT>.next :=
prewinner?/FONT>.next?/FONT>.next
{ remove winner from list }
end
end; { DELETEMIN }
Fig. 4.19. Linked list priority queue implementation.
children hold a and c. We assumed b ?/FONT> c, and we were told that a is larger than at least one of b and c. Therefore b ?/FONT> a surely holds. Thus the insertion procedure outlined above percolates an element down the tree until there
Fig. 4.20. A partially ordered tree.
are no more violations of the partially ordered property.Let us also observe that DELETEMIN applied to a set of n elements takes O(logn) time. This follows since no path in the tree has more than 1 + logn nodes, and the process of forcing an element down the tree takes a constant time per node. Observe that for any constant c, the quantity c(1+logn) is at most 2clogn for n ?/FONT> 2. Thus c(1+logn) is O(logn).
Now let us consider how INSERT should work. First, we place the new element as far left as possible on the lowest level, starting a new level if the current lowest level is all filled. Fig. 4.22(a) shows the result of placing an element with priority 4 into Fig. 4.20. If the new element has priority lower than its parent, exchange it with its parent. The new element is now at a position where it is of lower priority than either of its children, but it may also be of lower priority than its parent, in which case we must exchange it with its parent, and repeat the process, until the new element is either at the root or has larger priority than its parent. Figures 4.22(b) and (c) show how 4 moves up by this process.
We could prove that the above steps result in a partially ordered tree. While we shall not attempt a rigorous proof, let us observe that an element with priority a can become the parent of an element with priority b in three ways. (In what follows, we identify an element with its priority.)
Fig. 4.21. Pushing an element down the tree.
Fig. 4.22. Inserting an element.
parent of elements with priority 8 and 9. Originally, 5 was the parent of the former and the "grandparent" of the latter.The time to perform an insertion is proportional to the distance up the tree that the new element travels. As for DELETEMIN, we observe that this distance can be no greater than 1 + logn, so both INSERT and DELETEMIN take O(log n) steps.
The fact that the trees we have been considering are binary, balanced as much as possible, and have leaves at the lowest level pushed to the left means that we can use a rather unusual representation for these trees, called a heap. If there are n nodes, we use the first n positions of an array A. A [1] holds the root. The left child of the node in A[i], if it exists, is at A [2i], and the right child, if it exists, is at A [2i + 1]. An equivalent viewpoint is that the parent of A [i] is A [i div 2], for i > 1. Still another equivalent observation is that the nodes of a tree fill up A[1], A[2], . . . , A [n] level-by-level, from the top, and within a level, from the left. For example, Fig. 4.20 corresponds to an array containing the elements 3, 5, 9, 6, 8, 9, 10, 10, 18, 9.
We can declare a priority queue of elements of some type, say processtype as in Example 4.9, to consist of an array of processtype and an integer last, indicating the currently last element of the array that is in use. If we assume maxsize is the desired size of arrays for a priority queue, we can declare:
type
PRIORITYQUEUE = record
contents: array[1..maxsize] of processtype;
last: integer
end;
The priority queue operations are implemented below in Fig. 4.23.
procedure MAKENULL ( var A: PRIORITYQUEUE );
begin
A .last := 0
end; { MAKENULL }
procedure INSERT ( x: processtype; var A:
PRIORITYQUEUE );
var
i: integer;
temp : processtype;
begin
if A .last >= maxsize then
error ('priority queue is full')
else begin
A .last := A .last + 1;
A .contents [A .last] := x;
i := A .last; { i is index of current position of x }
while (i > 1) and†
(p(A .contents[i]) < p(A .contents[i
div 2])) do
begin { push x up the tree by exchanging it with its parent
of larger priority. Recall p computes the priority of
a processtype element }
temp := A .contents [i];
A .contents [i] := A .contents [i
div 2];
A .contents [i div 2] := temp;
i := i div 2
end
end
end; { INSERT }
function DELETEMIN ( var A: PRIORITYQUEUE ): ?/FONT> processtype;
var
i, j: integer;
temp : processtype;
minimum: ?/FONT> processtype;
begin
if A .last = 0 then
error('priority queue is empty')
else begin
new (minimum);
minimum ?/FONT> := A .contents
[1];
{ we shall return a pointer to a copy of the root of A }
A .contents [1] := A .contents [A .last];
A .last := A .last - 1;
{ move the last element to the beginning }
i := 1; { i is the current position of the old last element }
while i < = A .last div 2 do begin
{ push old last element down tree }
if (p (A .contents [2*i]) < p
(A .contents [2*i + 1]))
or (2*i = A.last) then
j := 2 * i
else
j := 2 * i + 1;
{ j will be the child of i having the smaller priority
or if 2*i = A.last, then j is the only child of i }
if p (A .contents [i]) > p (A
.contents [j]) then begin
{ exchange old last element with smaller priority child }
temp := A.contents[i];
A.contents[i] := A.contents[j];
A.contents[j] := temp;
i := j
end
else
return (minimum) { cannot push further }
end;
return (minimum) { pushed all the way to a leaf }
end
end; { DELETEMIN }
Fig. 4.23. Array implementation of priority queue.
In this section we consider two more complex uses of sets to represent data. The first problem is that of representing many-many relationships, as might occur in a database system. A second case study exhibits how a pair of data structures representing the same object (a mapping in our example) can be a more efficient representation than either acting alone.
An example of a many-many relationship between students and courses is suggested in Fig. 4.24. It is called a "many-many" relationship because there can be many students taking each course and many courses taken by each student.
Fig. 4.24. An example relationship between students and courses.
From time to time the registrar may wish to insert or delete students from courses, to determine which students are taking a given course, or to know which courses a given student is taking. The simplest data structure with which these questions can be answered is obvious; just use the 2-dimensional array suggested by Fig. 4.24, where the value 1 (or true) replaces the X's and 0 (or false) replaces the blanks.
For example, to insert a student into a course, we need a mapping,
MS,
perhaps implemented as a hash table, that translates student names into array
indices, and another, MC, that translates course names into array indices.
Then, to insert student s into course c, we simply set
Enrollment[MS(s
), MC(c)] := 1.
Deletions are performed by setting this element to 0. To find the courses taken by the student with name s, run across the row MS(s), and similarly run down the column MC(c) find the students in course c.
Why might we wish to look further for a more appropriate data structure? Consider a large university with perhaps 1000 courses and 20,000 students, taking an average of three courses each. The array suggested by Fig. 4.24 would have 20,000,000 elements, of which 60,000, or 0.3%, would be 1. † Such an array, which is called sparse to indicate that almost all its elements are zero, can be represented in far less space if we simply list the nonzero entries. Moreover, we can spend a great deal of time scanning a column of 20,000 entries searching for, on the average, 60 that are nonzero; row scans take considerable time as well.
One way to do better is to begin by phrasing the problem as one of
maintaining a collection of sets. Two of these sets are S and C, the sets of all
students and all courses. Each element of S is actually a record of a type such as
type
studenttype = record
id: integer;
name: array[l..30] of char;
end
and we would invent a similar record type for courses. To implement the
structure we have in mind, we need a third set of elements, E, standing for
enrollments. The elements of E each represent one of the boxes in the array
of Fig. 4.24 in which there is an X. The E elements are records of a fixed
type. As of now, we don't know any fields that belong in these records‡,
although we shall soon learn of them. For the moment, let us simply
postulate that there is an enrollment record for each X-entry in the array and that
enrollment records are distinguishable from one another somehow.
We also need sets that represent the answers to the crucial questions: given a student or course, what are the related courses or students, respectively. It would be nice if for each student s there were a set Cs of all the courses s was taking and conversely, a set Sc of the students taking course c.
Such sets would be hard to implement because there would be no limit on the number of sets any element could be in, forcing us to complicate student and course records. We could instead let Sc and Cs be sets of pointers to course and student records, rather than the records themselves, but there is a method that saves a significant fraction of the space and allows equally fast answers to questions about students and courses.
Let us make each set Cs be the set
of enrollment records corresponding to
student s and some course c. That is, if we think of an enrollment as a pair
(s, c), then
Cs = {(s, c) | s is taking course c}
We can similarly define
Sc = {(s,
c) | s is taking course c}
Note the only difference in the meaning of the two set formers above is that in the first case s is constant and in the second c is. For example, based on Fig. 4.24, CAlex = {(Alex, CS101), (Alex, CS202)} and SCS101 = {(Alex, CS101), (Amy, CS101), (Ann, CS101)}.
In general, a multilist structure is any collection of cells some of which have more than one pointer and can therefore be on more than one list simultaneously. For each type of cell in a multilist structure, it is important to distinguish among pointer fields so we can follow one particular list and not get confused about which of several pointers in a particular cell we are following.
As a case in point, we can put one pointer field in each student and course record, pointing to the first enrollment record in the set Cs or Sc, respectively. Each enrollment record needs two pointer fields, one, which we shall call cnext, for the next enrollment on the list for the Cs set to which it belongs and the other, snext, for the Sc set to which it belongs.
It turns out that an enrollment record indicates explicitly neither the student nor the course that it represents. The information is implicit in the lists on which the enrollment record appears. Call the student and course records heading these lists the owners of the enrollment record. Thus, to tell what courses student s is taking, we must scan the enrollment records in Cs and find for each one the owner course record. We could do that by placing a pointer in each enrollment record to the owning course record, and we would also need a pointer to the owning student record.
While we might wish to use these pointers and thereby answer questions in the minimum possible time, we can save substantial space† at the cost of slowing down some computations, if we eliminate these pointers and instead place at the end of each Sc list a pointer to the owning course and at the end of each Cs list a pointer to the owning student. Thus, each student and course record becomes part of a ring that includes all the enrollment records it owns. These rings are depicted in Fig. 4.25 for the data of Fig. 4.24. Note that each enrollment record has its cnext pointer first and its snext pointer second.
Fig. 4.25. Multilist representation of Fig. 4.24.
Example 4.11. To answer a question like "which students are taking CS101," we find the course record for CS101. How we find such a record depends on how the set of courses is maintained. For example, there might be a hash table containing all such records, and we obtain the desired record by applying some hash function to "CS101".
We follow the pointer in the CS101 record to the first enrollment record in the ring for CS101. This is the second enrollment record from the left. We must then find the student owner of this enrollment record, which we do by following cnext pointers (the first pointer in enrollment records) until we reach a student record.† In this case, we reach the third enrollment record, then the student record for Alex; we now know that Alex is taking CS101.
Now we must find the next student in CS101. We do so by following the snext pointer (second pointer) in the second enrollment record, which leads to the fifth enrollment record. The cnext pointer in that record leads us directly to the owner, Amy, so Amy is in CS101. Finally, we follow the snext pointer in the fifth enrollment record to the eighth enrollment record. The ring of cnext pointers from that record leads to the ninth enrollment record, then to the student record for Ann, so Ann is in CS101. The snext pointer in the eighth enrollment record leads back to CS101, so we are done.
Abstractly, we can express the operation in Example 4.11 above
as
for each enrollment
record in the set for CS101 do begin
s := the student owner of the enrollment record;
print(s)
end
The above assignment to s can be elaborated as
f := e;
repeat
f := f?/FONT>.cnext
until
f is a pointer to a student record;
s := studentname
field of record pointed to by f;
where e is a pointer to the first enrollment record in the set for CS101.
In order to implement a structure like Fig. 4.25 in Pascal, we need to have only one record type, with variants to cover the cases of student, course, and enrollment records. Pascal forces this arrangement on us since the fields cnext and snext each have the ability to point to different record types. This arrangement, however, does solve one of our other problems. It is now easy to tell what type of record we have reached as we travel around a ring. Figure 4.26 shows a possible declaration of the records and a procedure that prints the students taking a particular class.
Often, a seemingly simple representation problem for a set or mapping presents a difficult problem of data structure choice. Picking one data structure for the set makes certain operations easy, but others take too much time, and it seems that there is no one data structure that makes all the operations easy. In that case, the solution often turns out to be the use of two or more different structures for the same set or mapping.
Suppose we wish to maintain a "tennis ladder," in which each player is on a unique "rung." New players are added to the bottom, that is, the highest- numbered rung. A player can challenge the player on the rung above, and if the player below wins the match, they trade rungs. We can represent this situation as an abstract data type, where the underlying model is a mapping from names (character strings) to rungs (integers 1, 2, . . . ). The three operations we perform are
type
stype = array[l..20] of char;
ctype = array[1..5] of char;
recordkinds = (student, course, enrollment);
recordtype = record
case kind: recordkinds of
student: (studentname: stype;
firstcourse: ?/FONT> recordtype);
course: (coursename: ctype;
firststudent: ?/FONT> recordtype);
enrollment: (cnext, snext: ?/FONT> recordtype)
end;
procedure printstudents ( cname: ctype );
var
c, e, f: ?/FONT> recordtype;
begin
c := pointer to course record with c?/FONT>.coursename = cname;
{ above depends on how course set is implemented }
e := c ?/FONT>.firststudent;
{ e runs around the ring of enrollments pointed to by c }
while e ?/FONT>.kind =
enrollment do begin
f := e;
repeat
f := f?/FONT>.cnext
until
f?/FONT>.kind = student;
{ f now points to student owner of enrollment e ?/FONT> }
writeln (f?/FONT>.studentname ) ;
e := e?/FONT>.snext
end
end
Fig. 4.26. Implementation of search through a multilist.
Notice that we have chosen to pass only the higher rung number to EXCHANGE, while the other two operations take a name as argument.
We might, for example, choose an array LADDER, where LADDER[i] is the name of the person on rung i. If we also keep a count of the number of players, adding a player to the first unoccupied rung can be done in some small constant number of steps.
EXCHANGE is also easy, as we simply swap two elements of the array. However, CHALLENGE(name) requires that we examine the entire array for the name, which takes O(n) time, if n is the number of players on the ladder.
On the other hand, we might consider a hash table to represent the mapping from names to rungs. On the assumption that we can keep the number of buckets roughly proportional to the number of players, ADD takes O(1) time, on the average. Challenging takes O(1) time on the average to look up the given name, but O(n) time to find the name on the next lower-numbered rung, since the entire hash table may have to be searched. Exchanging requires O(n) time to find the players on rungs i and i - 1.
Suppose, however, that we combine the two structures. The cells of the hash table will contain pairs consisting of a name and a rung, while the array will have in LADDER[i] a pointer to the cell for the player on rung i as suggested in Fig. 4.27.
Fig. 4.27. Combined structure for high performance.
We can add a name by inserting into the hash table in O(1) time on the average, and also placing a pointer to the newly created cell into the array LADDER at a position marked by the cursor nextrung in Fig. 4.27. To challenge, we look up the name in the hash table, taking O(1) time on the average, get the rung i for the given player, and follow the pointer in LADDER[i-1] to the cell of the hash table for the player to be challenged. Consulting LADDER[i - 1] takes constant time in the worst case, and the lookup in the hash table takes O(1) time on the average, so CHALLENGE is O(1) in the average case.
EXCHANGE(i) takes O(1) time to find the cells for the players on rungs i and i-l, swap the rung numbers in those cells, and swap the pointers to the two cells in LADDER. Thus EXCHANGE requires constant time in even the worst case.
| 4.1 | If A = {1, 2, 3} and B = {3, 4, 5}, what are the results of
|
|---|---|
| *4.2 | Write a procedure in terms of the basic set operations to print all the elements of a (finite) set. You may assume that a procedure to print an object of the element type is available. You must not destroy the set you are printing. What data structures would be most suitable for implementing sets in this case? |
| 4.3 | The bit-vector implementation of sets can be used whenever the
"universal set" can be translated into the integers 1 through N.
Describe how this translation would be done if the universal set were
|
| 4.4 | Write MAKENULL, UNION, INTERSECTION, MEMBER, MIN, INSERT, and DELETE procedures for sets represented by lists using the abstract operations for the sorted list ADT. Note that Fig. 4.5 is a procedure for INTERSECTION using a specific implementation of the list ADT. |
| 4.5 | Repeat Exercise 4.4 for the following set implementations:
|
| 4.6 | For each of the operations and each of the implementations in Exercises 4.4 and 4.5, give the order of magnitude for the running time of the operations on sets of size n. |
| 4.7 | Suppose we are hashing integers with a 7-bucket hash table using the
hash function h(i) = i mod 7.
|
| 4.8 | Suppose we are using a closed hash table with 5 buckets and the hashing function h(i) = i mod 5. Show the hash table that results with linear resolution of collisions if the sequence 23, 48, 35, 4, 10 is inserted into an initially empty table. |
| 4.9 | Implement the mapping ADT operations using open and closed hash tables. |
| 4.10 | To improve the speed of operations, we may wish to replace an open hash table with B1 buckets holding many more than B1 elements by another hash table with B2 buckets. Write a procedure to construct the new hash table from the old, using the list ADT operations to process each bucket. |
| 4.11 | In Section 4.8 we discussed "random" hash functions, where hi(x),
the bucket to be tried after i collisions, is (h (x) + di)
mod B for some
sequence d1, d2, . . . ,dB-1.
We also suggested that one way to
compute a suitable sequence d 1, d2, . . . ,
dB-1 was to pick a
constant k, an arbitrary d1 > 0, and let
|
| 4.12 |
|
| 4.13 | Suppose we represent the set of courses by
Modify the declarations in Fig. 4.26 for each of these structures. |
| 4.14 | Modify the data structure of Fig. 4.26 to give each enrollment record a direct pointer to its student and course owners. Rewrite the procedure printstudents of Fig. 4.26 to take advantage of this structure. |
| 4.15 | Assuming 20,000 students, 1,000 courses, and each student in an
average of three courses, compare the data structure of Fig. 4.26 with
its modification suggested in Exercise 4.14 as to
|
| 4.16 | Assuming the data structure of Fig. 4.26, given course record c and student record s, write procedures to insert and to delete the fact that s is taking c. |
| 4.17 | What, if anything, is the difference between the data structure of Exercise 4.14 and the structure in which sets Cs and Sc are represented by lists of pointers to course and student records, respectively? |
| 4.18 | Employees of a certain company are represented in the company data base by their name (assumed unique), employee number, and social security number. Suggest a data structure that lets us, given one representation of an employee, find the other two representations of the same individual. How fast, on the average, can you make each such operation? |
Knuth [1973] is a good source for additional information on hashing. Hashing was developed in the mid-to-late 1950's, and Peterson [1957] is a fundamental early paper on the subject. Morris [1968] and Maurer and Lewis [1975] are good surveys of hashing.
The multilist is a central data structure of the network-based database systems proposed in DBTG [1971]. Ullman [1982] provides additional information on database applications of structures such as these.
The heap implementation of partially ordered trees is based on an idea in Williams [1964]. Priority queues are discussed further in Knuth [1973].
Reingold [1972] discusses the computational complexity of basic set operations. Set-based data flow analysis techniques are treated in detail in Cocke and Allen [1976] and Aho and Ullman [1977].
†Sometimes the term multiset is used for a "set with repetitions." That is, the multiset {1, 4, 1} has 1 (twice) and 4 (once) as members. A multiset is not a list any more than a set is, and thus this multiset could also have been written {4, 1, 1} or {1, 1, 4}.
†Changes to the data structure can be made that will speed up open hashing and allow closed hashing to handle larger sets. We shall describe these techniques after giving the basic methods.
†If the type of members of the dictionary does not suggest an appropriate value for empty, let each bucket have an extra one-bit field to tell whether or not it is empty.
†Note that A2 and A20 do not necessarily hash to the same bucket, but A23 and A41, for example, must do so.
†If strings can be extremely long, this addition will have to be performed modulo some constant c. For example, c could be one more than the largest integer obtainable from a single block.
†If this were a real database system, the array would be kept in secondary storage. However, this data structure would waste a great deal of space.
†Note that there are probably many more enrollment records than course or student records, so shrinking enrollment records shrinks the total space requirement almost as much.
‡It would in practice be useful to place fields like grade or status (credit or audit) in enrollment records, but our original problem statement does not require this.
†We must have some way of identifying the type of records; we shall discuss a way to do this momentarily.
†We assume this and is a conditional and.
