



This chapter introduces data structures for sets that permit more efficient implementation of common collections of set operations than those of the previous chapter. These structures, however, are more complex and are often only appropriate for large sets. All are based on various kinds of trees, such as binary search trees, tries, and balanced trees.
We shall begin with binary search trees, a basic data structure for representing sets whose elements are ordered by some linear order. We shall, as usual, denote that order by <. This structure is useful when we have a set of elements from a universe so large that it is impractical to use the elements of the set themselves as indices into arrays. An example of such a universe would be the set of possible identifiers in a Pascal program. A binary search tree can support the set operations INSERT, DELETE, MEMBER, and MIN, taking O(logn) steps per operation on the average for a set of n elements.
A binary search tree is a binary tree in which the nodes are labeled with elements of a set. The important property of a binary search tree is that all elements stored in the left subtree of any node x are all less than the element stored at x, and all elements stored in the right subtree of x are greater than the element stored at x. This condition, called the binary search tree property, holds for every node of a binary search tree, including the root.
Figure 5.1 shows two binary search trees representing the same set of integers. Note the interesting property that if we list the nodes of a binary search tree in inorder, then the elements stored at those nodes are listed in sorted order.
Suppose a binary search tree is used to represent a set. The binary search tree property makes testing for membership in the set simple. To determine whether x is a member of the set, first compare x with the element r at the root of the tree. If x = r we are done and the answer to the membership query is "true." If x < r, then by the binary search tree property, x can only
Fig. 5.1. Two binary search trees.
be a descendant of the left child of the root, if x is present at all.† Similarly, if x > r, then x could only be at a descendant of the right child of the root.We shall write a simple recursive function MEMBER(x, A) to implement this membership test. We assume the elements of the set are of an unspecified type that will be called elementtype. For convenience, we assume elementtype is a type for which < and = are defined. If not, we must define functions LT(a, b) and EQ(a, b), where a and b are of type elementtype, such that LT(a, b) is true if and only if a is "less than" b, and EQ(a, b) is true if and only if a and b are the same.
The type for nodes consists of an element and two pointers to other nodes:
type nodetype = record element: elementtype; leftchild, rightchild: ?/FONT> nodetype end;
Then we can define the type SET as a pointer to a node, which we take to be the root of the binary search tree representing the set. That is:
type SET = ?/FONT> nodetype;
Now we can specify fully the function MEMBER, in Fig. 5.2. Notice that since SET and "pointer to nodetype" are synonymous, MEMBER can call itself on subtrees as if those subtrees represented sets. In effect, the set can be subdivided into the subset of members less than x and the subset of members greater than x.
function MEMBER ( x: elementtype; A: SET ): boolean,
{ returns true if x is in A, false otherwise }
begin
if A = nil then
return (false) { x is never in Ø }
else if x = A ?/FONT>.element then
return (true)
else if x < A ?/FONT>.element then
return (MEMBER(x, A ?/FONT>.leftchild ) )
else { x > A ?/FONT>.element }
return (MEMBER(x, A ?/FONT>.rightchild ) )
end; { MEMBER }
The procedure INSERT(x, A), which adds element x to set A, is also easy to write. The first action INSERT must do is test whether A = nil, that is, whether the set is empty. If so, we create a new node to hold x and make A point to it. If the set is not empty, we search for x more or less as MEMBER does, but when we find a nil pointer during our search, we replace it by a pointer to a new node holding x. Then x will be in the right place, namely, the place where the function MEMBER will find it. The code for INSERT is shown in Fig. 5.3.
Deletion presents some problems. First, we must locate the element x to be deleted in the tree. If x is at a leaf, we can delete that leaf and be done. However, x may be at an interior node inode, and if we simply deleted inode, we would disconnect the tree.
If inode has only one child, as the node numbered 14 in Fig. 5.1(b), we can replace inode by that child, and we shall be left with the appropriate binary search tree. If inode has two children, as the node numbered 10 in Fig. 5.1(a), then we must find the lowest-valued element among the descendants of the right child.† For example, in the case the element 10 is deleted from Fig. 5.1(a), we must replace it by 12, the minimum-valued descendant of
procedure INSERT ( x: elementtype; var A: SET );
{ add x to set A }
begin
if A = nil then begin
new (A);
A ?/FONT> .element: = x;
A ?/FONT> .leftchild := nil;
A ?/FONT> .rightchild: = nil
end
else if x < A ?/FONT>.element
then
INSERT(x, A ?/FONT>.leftchild)
else if x > A ?/FONT>.element
then
INSERT (x, A ?/FONT>.rightchild)
{ if x = A ?/FONT>.element, we do
nothing; x is already in the set }
end; { INSERT }
To write DELETE, it is useful to have a function DELETEMIN(A) that removes the smallest element from a nonempty tree and returns the value of the element removed. The code for DELETEMIN is shown in Fig. 5.4. The code for DELETE uses DELETEMIN and is shown in Fig. 5.5.
function DELETEMIN ( var A: SET ): elementtype;
{ returns and removes the smallest element from set A }
begin
if A ?/FONT>.leftchild = nil then
begin
{ A points to the smallest element }
DELETEMIN := A ?/FONT>.element;
A := A ?/FONT>.rightchild
{ replace the node pointed to by A by its right child }
end
else { the node pointed to by A has a left child }
DELETEMIN := DELETEMIN(A ?/FONT>.leftchild)
end; { DELETEMIN }
Example 5.1. Suppose we try to delete 10 from Fig. 5.1(a). Then, in the last statement of DELETE we call DELETEMIN with argument a pointer to node 14. That pointer is the rightchild field in the root. That call results in another call to DELETEMIN. The argument is then a pointer to node 12; this pointer is found in the leftchild field of node 14. We find that 12 has no
procedure DELETE ( x: elementtype; var A: SET );
{ remove x from set A }
begin
if A < > nil then
if x < A ?/FONT>.element
then
DELETE(x, A ?/FONT>.leftchild)
else if x > A ?/FONT>.element then
DELETE(x, A ?/FONT>.rightchild)
{ if we reach here, x is at the node pointed to by A }
else if (A ?/FONT>.leftchild =
nil) and (A ?/FONT>.rightchild =
nil) then
A := nil { delete the leaf holding x }
else if A ?/FONT>.leftchild =
nil then
A := A ?/FONT>.rightchild
else if A ?/FONT>.rightchild =
nil then
A := A ?/FONT>.leftchild
else { both children are present }
A ?/FONT>.element :=
DELETEMIN(A ?/FONT>.rightchild)
end; { DELETE }
In this section we analyze the average behavior of various binary search tree operations. We show that if we insert n random elements into an initially empty binary search tree, then the average path length from the root to a leaf is O(logn). Testing for membership, therefore, takes O(logn) time.
It is easy to see that if a binary tree of n nodes is complete (all nodes, except those at the lowest level have two children), then no path has more than 1+logn nodes.† Thus, each of the procedures MEMBER, INSERT, DELETE, and DELETEMIN takes O(logn) time. To see this, observe that they all take a constant amount of time at a node, then may call themselves recursively on at most one child. Therefore, the sequence of nodes at which calls are made forms a path from the root. Since that path is O(logn) in length, the total time spent following the path is O(logn).
However, when we insert n elements in a "random" order,
they do not
necessarily arrange themselves into a complete binary tree. For example, if
we happen to insert smallest first, in sorted order, then the resulting tree is a
chain of n nodes, in which each node except the lowest has a right child but
no left child. In this case, it is easy to show that, as it takes O(i) steps to
insert the ith element, and
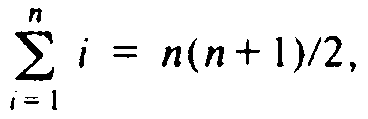 , the
whole process of n insertions
takes O(n2) steps, or O(n) steps per operation.
, the
whole process of n insertions
takes O(n2) steps, or O(n) steps per operation.
We must determine whether the "average" binary search tree of n nodes is closer to the complete tree in structure than to the chain, that is, whether the average time per operation on a "random" tree takes O(logn) steps, O(n) steps, or something in between. As we cannot know the true frequency of insertions and deletions, or whether deleted elements have some special property (e.g., do we always delete the minimum?), we can only analyze the average path length of "random" trees if we make some assumptions. The particular assumptions we make are that trees are formed by insertions only, and all orders of the n inserted elements are equally likely.
Under these fairly natural assumptions, we can calculate P(n), the average number of nodes on the path from the root to some node (not necessarily a leaf). We assume the tree was formed by inserting n random elements into an initially empty tree. Clearly P(0) = 0 and P(1) = 1. Suppose we have a list of n?/FONT>2 elements to insert into an empty tree. The first element on the list, call it a, is equally likely to be first, second, or nth in the sorted order. Suppose that i elements on the list are less than a, so n-i-1 are greater than a. When we build the tree, a will appear at the root, the i smaller elements will be descendants of the left child of the root, and the remaining n-i-1 will be descendants of the right child. This tree is sketched in Fig. 5.7.
As all orders for the i small elements and for the n-i-1 large elements are equally likely, we expect that the left and right subtrees of the root will

The first term is the average path length in the left subtree, weighted by its size. The second term is the analogous quantity for the right subtree, and the 1/n term represents the contribution of the root. By averaging the above sum for all i between 1 and n, we obtain the recurrence

The first part of the summation (5.1),
 , can be made identical to
the second part
, can be made identical to
the second part
 if we substitute i
for n-i-1 in the
second part. Also, the term for i=0 in the summation
if we substitute i
for n-i-1 in the
second part. Also, the term for i=0 in the summation
 is zero, so we
can begin the summation at 1. Thus (5.1) can be written
is zero, so we
can begin the summation at 1. Thus (5.1) can be written

We shall show by induction on n, starting at n=1, that P(n) ?/FONT> 1 + 4logn. Surely this statement is true for n = 1, since P(1) = 1. Suppose it is true for all i < n. Then by (5.2)


The last step is justified, since
 , and
therefore, the last term of the
second line is at most 1. We shall divide the terms in the summation of (5.3)
into two parts, those for i ?/FONT> [n/2]-1, which do not
exceed ilog(n/2), and
those for i> [n/2]-1, which do not exceed ilogn. Thus (5.3) can be
rewritten
, and
therefore, the last term of the
second line is at most 1. We shall divide the terms in the summation of (5.3)
into two parts, those for i ?/FONT> [n/2]-1, which do not
exceed ilog(n/2), and
those for i> [n/2]-1, which do not exceed ilogn. Thus (5.3) can be
rewritten

Whether n is even or odd, one can show that the first sum of (5.4) does not exceed (n2/8)log(n/2), which is (n2/8)logn - (n2/8), and the second sum does not exceed (3n2/8)logn. Thus, we can rewrite (5.4) as

We can conclude from the above that the time of membership testing for a random member of the set takes O(logn) time. A similar analysis shows that if we include in our average path length only those nodes that are missing both children, or only those missing left children, then the average path length still obeys an equation similar to (5.1), and is therefore O(logn). We may then conclude that testing membership of a random element not in the set, inserting a random new element, and deleting a random element also all take O(logn) time on the average.
Hash table implementations of dictionaries require constant time per operation on the average. Although this performance is better than that for a binary search tree, a hash table requires O(n) steps for the MIN operation, so if MIN is used frequently, the binary search tree will be the better choice; if MIN is not needed, we would probably prefer the hash table.
The binary search tree should also be compared with the partially ordered tree used for priority queues in Chapter 4. A partially ordered tree with n elements requires only O(logn) steps for each INSERT and DELETEMIN operation not only on the average, but also in the worst case. Moreover, the actual constant of proportionality in front of the logn factor will be smaller for a partially ordered tree than for a binary search tree. However, the binary search tree permits general DELETE and MIN operations, as well as the combination DELETEMIN, while the partially ordered tree permits only the latter. Moreover, MEMBER requires O(n) steps on a partially ordered tree but only O(logn) steps on a binary search tree. Thus, while the partially ordered tree is well suited to implementing priority queues, it cannot do as efficiently any of the additional operations that the binary search tree can do.
In this section we shall present a special structure for representing sets of character strings. The same method works for representing data types that are strings of objects of any type, such as strings of integers. This structure is known as the trie, derived from the middle letters of the word "retrieval." † By way of introduction, consider the following use of a set of character strings.
Example 5.2. As indicated in Chapter 1, one way to implement a spelling checker is to read a text file, break it into words (character strings separated by blanks and new lines), and find those words not in a standard dictionary of words in common use. Words in the text but not in the dictionary are printed out as possible misspellings. In Fig. 5.8 we see a sketch of one possible program spell. It makes use of a procedure getword(x, f) that sets x to be the next word in text file f; variable x is of a type called wordtype, which we shall define later. The variable A is of type SET; the SET operations we shall need are INSERT, DELETE, MAKENULL, and PRINT. The PRINT operator prints the members of the set.
The trie structure supports these set operations when the elements of the set are words, i.e., character strings. It is appropriate when many words begin with the same sequences of letters, that is, when the number of distinct prefixes among all the words in the set is much less than the total length of all the words.
In a trie, each path from the root to a leaf corresponds to one word in the represented set. This way, the nodes of the trie correspond to the prefixes of words in the set. To avoid confusion between words like THE and THEN, let us add a special endmarker symbol, $, to the ends of all words, so no prefix of a word can be a word itself.
Example 5.3. In Fig. 5.9 we see a trie representing the set of words {THE, THEN, THIN, THIS, TIN, SIN, SING}. That is, the root corresponds to the empty string, and its two children correspond to the prefixes T and S. The
program spell ( input, output, dictionary );
type
wordtype = { to be defined };
SET = { to be defined, using the trie structure };
var
A: SET; { holds input words not yet found in the dictionary }
nextword: wordtype;
dictionary: file of char;
procedure getword ( var x: wordtype; f: file
of char );
{ a procedure to be defined that sets x
to be the next word in file f}
procedure INSERT ( x: wordtype; var S: SET );
{ to be defined }
procedure DELETE (x: wordtype; var S: SET );
{ to be defined }
procedure MAKENULL ( var S: SET );
{ to be defined }
procedure PRINT ( var S: SET );
{ to be defined }
begin
MAKENULL(A);
while not eof(input) do begin
getword ( nextword, input);
INSERT(nextword, A)
end;
while not eof (dictionary) do begin
getword ( nextword, dictionary);
DELETE(nextword, A)
end;
PRINT(A)
end; { spell }
We can make the following observations about the trie in Fig. 5.9.
We can view a node of a trie as a mapping whose domain is {A, B, ... , Z, $} (or whatever alphabet we choose) and whose value set is the type "pointer to trie node." Moreover, the trie itself can be identified with its root, so the ADT's TRIE and TRIENODE have the same data type, although their operations are substantially different. On TRIENODE we need the following operations:
Technically, we also need a procedure MAKENULL(node) to make node be the null mapping. One simple implementation of trie nodes is an array node of pointers to nodes, with the index set being {A, B, ..., Z, $}. That is, we define
type
chars = ('A', 'B', ... , 'Z', '$');
TRIENODE = array[chars] of ?/FONT>;
TRIENODE;
If node is a trie node, node[c] is VALUEOF(node, c) for any c in the set chars. To avoid creating many leaves that are children corresponding to '$', we shall adopt the convention that node['$'] is either nil or a pointer to the node itself. In the former case, node has no child corresponding to '$', and in the latter case it is deemed to have such a child, although we never create it. Then we can write the procedures for trie nodes as in Fig. 5.10.
procedure MAKENULL ( var node: TRIENODE );
{ makes node a leaf, i.e., a null mapping }
var
c: chars;
begin
for c: = 'A' to '$' do
node [c] := nil
end; { MAKENULL }
procedure ASSIGN ( var node: TRIENODE; c: chars;
p: ?/FONT> TRIENODE );
begin
node [c] := p
end; { ASSIGN }
function VALUEOF ( var node: TRIENODE; c: chars ):
?/FONT> TRIENODE;
begin
return (node [c])
end; { VALUEOF }
procedure GETNEW ( var node: TRIENODE; c: chars );
begin
new (node [c]);
MAKENULL(node [c])
end; { GETNEW }
Now let us define
type TRIE = ?/FONT> TRIENODE;
We shall assume wordtype is an array of characters of some fixed length. The value of such an array will always be assumed to have at least one '$'; we take the end of the represented word to be the first '$', no matter what follows (presumably more '$' 's). On this assumption, we can write the procedure INSERT(x, words) to insert x into set words represented by a trie, as shown in Fig. 5.11. We leave the writing of MAKENULL, DELETE, and PRINT for tries represented as arrays for exercises.
procedure INSERT ( x: wordtype; var words: TRIE );
var
i: integer; { counts positions in word x }
t: TRIE; { used to point to trie nodes
corresponding to prefixes of x }
begin
i : = 1;
t := words;
while x[i] <> '$' do begin
if VALUEOF(t?/FONT>,
x[i]) = nil then
{ if current node has no child for character x[i],
create one }
GETNEW(t?/FONT>, x[i]);
t := VALUEOF(t?/FONT>,
x[i]);
{ proceed to the child of t for character x[i],
whether or not that child was just created }
i := i+1 { move along the word x }
end;
{ now we have reached the first '$' in x }
ASSIGN(t?/FONT>, '$', t)
{ make loop for '$' to represent a leaf }
end; {INSERT}
The array representation of trie nodes takes a collection of words, having among them p different prefixes, and represents them with 27p bytes of storage. That amount of space could far exceed the total length of the words in the set. However, there is another implementation of tries that may save space. Recall that each trie node is a mapping, as discussed in Section 2.6. In principle, any implementation of mappings would do. Yet in practice, we want a representation suitable for mappings with a small domain and for mappings defined for comparatively few members of that domain. The linked list representation for mappings satisfies these requirements nicely. We may represent the mapping that is a trie node by a linked list of the characters for which the associated value is not the nil pointer. That is, a trie node is a linked list of cells of the type
type
celltype = record
domain: chars;
value: ?/FONT> celltype;
{ pointer to first cell on list for the child node }
next: ?/FONT> celltype
{ pointer to next cell on the list }
end;
We shall leave the procedures ASSIGN, VALUEOF, MAKENULL, and GETNEW for this implementation of trie nodes as exercises. After writing these procedures, the INSERT operations on tries, in Fig. 5.11, and the other operations on tries that we left as exercises, should work correctly.
Let us compare the time and space needed to represent n words with a total of p different prefixes and a total length of l using a hash table and a trie. In what follows, we shall assume that pointers require four bytes. Perhaps the most space-efficient way to store words and still support INSERT and DELETE efficiently is in a hash table. If the words are of varying length, the cells of the buckets should not contain the words themselves; rather, the cells consist of two pointers, one to link the cells of the bucket and the other pointing to the beginning of a word belonging in the bucket.
The words themselves are stored in a large character array, and the end of each word is indicated by an endmarker character such as '$'. For example, the words THE, THEN, and THIN could be stored as
The pointers for the three words are cursors to positions 1, 5, and 10 of the array. The amount of space used in the buckets and character array is
The total space is thus 9n + l bytes plus whatever amount is used for the bucket headers.
In comparison, a trie with nodes implemented by linked lists requires p + n cells, one cell for each prefix and one cell for the end of each word. Each trie cell has a character and two pointers, and needs nine bytes, for a total space of 9n + 9p. If l plus the space for the bucket headers exceeds 9p, the trie uses less space. However, for applications such as storing a dictionary where l/p is typically less than 3, the hash table would use less space.
In favor of the trie, however, let us note that we can travel down a trie, and thus perform operations INSERT, DELETE, and MEMBER in time proportional to the length of the word involved. A hash function to be truly "random" should involve each character of the word being hashed. It is fair, therefore, to state that computing the hash function takes roughly as much time as performing an operation like MEMBER on the trie. Of course the time spent computing the hash function does not include the time spent resolving collisions or performing the insertion, deletion, or membership test on the hash table, so we can expect tries to be considerably faster than hash tables for dictionaries whose elements are character strings.
Another advantage to the trie is that it supports the MIN operation efficiently, while hash tables do not. Further, in the hash table organization described above, we cannot easily reuse the space in the character array when a word is deleted (but see Chapter 12 for methods of handling such a problem).
In Sections 5.1 and 5.2 we saw how sets could be implemented by binary search trees, and we saw that operations like INSERT could be performed in time proportional to the average depth of nodes in that tree. Further, we discovered that this average depth is O(logn) for a "random" tree of n nodes. However, some sequences of insertions and deletions can produce binary search trees whose average depth is proportional to n. This suggests that we might try to rearrange the tree after each insertion and deletion so that it is always complete; then the time for INSERT and similar operations would always be O(logn).
In Fig. 5.12(a) we see a tree of six nodes that becomes the complete tree of seven nodes in Fig. 5.12(b), when element 1 is inserted. Every element in Fig. 5.12(a), however, has a different parent in Fig. 5.12(b), so we must take n steps to insert 1 into a tree like Fig. 5.12(a), if we wish to keep the tree as balanced as possible. It is thus unlikely that simply insisting that the binary search tree be complete will lead to an implementation of a dictionary, priority queue, or other ADT that includes INSERT among its operations, in O(logn) time.
There are several other approaches that do yield worst case O(logn) time per operation for dictionaries and priority queues, and we shall consider one of them, called a "2-3 tree," in detail. A 2-3 tree is a tree with the following two properties.
We shall also consider a tree with zero nodes or one node as special cases of a 2-3 tree.
We represent sets of elements that are ordered by some linear order <, as follows. Elements are placed at the leaves; if element a is to the left of
At each interior node we record the key of the smallest element that is a descendant of the second child and, if there is a third child, we record the key of the smallest element descending from that child as well.† Figure 5.13 is an example of a 2-3 tree. In that and subsequent examples, we shall identify an element with its key field, so the order of elements becomes obvious.
Observe that a 2-3 tree of k levels has between 2k-1 and 3k-1 leaves. Put another way, a 2-3 tree representing a set of n elements requires at least 1 + log3n levels and no more than 1 + log2n levels. Thus, path lengths in the tree are O(logn).
We can test membership of a record with key x in a set represented by a 2-3 tree in O(logn) time by simply moving down the tree, using the values of the elements recorded at the interior nodes to guide our path. At a node node, compare x with the value y that represents the smallest element descending from the second child of node. (Recall we are treating elements as if they consisted solely of a key field.) If x < y, move to the first child of node. If x?/FONT>y, and node has only two children, move to the second child of node. If node has three children and x?/FONT>y, compare x with z, the second value recorded at node, the value that indicates the smallest descendant of the third child of node. If x<z, go to the second child, and if x?/FONT>z, go to the third child. In this manner, we find ourselves at a leaf eventually, and x is in the represented set if and only if x is at the leaf. Evidently, if during this process we find x=y or x=z, we can stop immediately. However, we stated the algorithm as we did because in some cases we shall wish to find the leaf with x as well as to verify its existence.
To insert a new element x into a 2-3 tree, we proceed at first as if we were testing membership of x in the set. However, at the level just above the leaves, we shall be at a node node whose children, we discover, do not include x. If node has only two children, we simply make x the third child of node, placing the children in the proper order. We then adjust the two numbers at node to reflect the new situation.
For example, if we insert 18 into Fig. 5.13, we wind up with node equal to the rightmost node at the middle level. We place 18 among the children of node, whose proper order is 16, 18, 19. The two values recorded at node become 18 and 19, the elements at the second and third children. The result is shown in Fig. 5.14.
Suppose, however, that x is the fourth, rather than the third child of node. We cannot have a node with four children in a 2-3 tree, so we split node into two nodes, which we call node and node'. The two smallest elements among the four children of node stay with node, while the two larger elements become children of node'. Now, we must insert node' among the children of p, the parent of node. This part of the insertion is analogous to the insertion of a leaf as a child of node. That is, if p had two children, we make node' the third and place it immediately to the right of node. If p had three children before node' was created, we split p into p and p', giving p the two leftmost children and p' the remaining two, and then we insert p' among the children of p's parent, recursively.
One special case occurs when we wind up splitting the root. In that case we create a new root, whose two children are the two nodes into which the
Example 5.4. Suppose we insert 10 into the tree of Fig. 5.14. The intended parent of 10 already has children 7, 8, and 12, so we split it into two nodes. The first of these has children 7 and 8; the second has 10 and 12. The result is shown in Fig. 5.15(a). We must now insert the new node with children 10 and 12 in its proper place as a child of the root of Fig. 5.15(a). Doing so gives the root four children, so we split it, and create a new root, as shown in Fig. 5.15(b). The details of how information regarding smallest elements of subtrees is carried up the tree will be given when we develop the program for the command INSERT.
When we delete a leaf, we may leave its parent node with only one child. If node is the root, delete node and let its lone child be the new root. Otherwise, let p be the parent of node. If p has another child, adjacent to node on either the right or the left, and that child of p has three children, we can transfer the proper one of those three to node. Then node has two children, and we are done.
If the children of p adjacent to node have only two children, transfer the lone child of node to an adjacent sibling of node, and delete node. Should p now have only one child, repeat all the above, recursively, with p in place of node.
Example 5.5. Let us begin with the tree of Fig. 5.15(b). If 10 is deleted, its parent has only one child. But the grandparent has another child that has three children, 16, 18, and 19. This node is to the right of the deficient node, so we pass the deficient node the smallest element, 16, leaving the 2-3 tree in Fig. 5.16(a).
Next suppose we delete 7 from the tree of Fig. 5.16(a). Its parent now has only one child, 8, and the grandparent has no child with three children. We therefore make 8 be a sibling of 2 and 5, leaving the tree of Fig. 5.16(b). Now the node starred in Fig. 5.16(b) has only one child, and its parent has no other child with three children. Thus we delete the starred node, making its child be a child of the sibling of the starred node. Now the root has only one child, and we delete it, leaving the tree of Fig. 5.16(c).
Observe in the above examples, the frequent manipulation of the values at interior nodes. While we can always calculate these values by walking the tree, it can be done as we manipulate the tree itself, provided we remember the smallest value among the descendants of each node along the path from the root to the deleted leaf. This information can be computed by a recursive deletion algorithm, with the call at each node being passed, from above, the correct quantity (or the value "minus infinity" if we are along the leftmost path). The details require careful case analysis and will be sketched later when we consider the program for the DELETE operation.
Let us restrict ourselves to representing by 2-3 trees sets of elements whose keys are real numbers. The nature of other fields that go with the field key, to make up a record of type elementtype, we shall leave unspecified, as it has no bearing on what follows.
In Pascal, the parents of leaves must be records of consisting of two reals (the key of the smallest elements in the second and third subtrees) and of three pointers to elements. The parents of these nodes are records consisting of two reals and of three pointers to parents of leaves. This progression continues indefinitely; each level in a 2-3 tree is of a different type from all other levels. Such a situation would make programming 2-3 tree operations in Pascal impossible, but fortunately, Pascal provides a mechanism, the variant record structure, that enables us to regard all 2-3 tree nodes as having the same type, even though some are elements, and some are records with pointers and reals.† We can define nodes as in Fig. 5.17. Then we declare a set, represented by a 2-3 tree, to be a pointer to the root as in Fig. 5.17.
The details of operations on 2-3 trees are quite involved, although the principles are simple. We shall therefore describe only one operation, insertion, in detail; the others, deletion and membership testing, are similar in spirit, and finding the minimum is a trivial search down the leftmost path. We shall write the insertion routine as main procedure, INSERT, which we call at the root, and a procedure insert 1, which gets called recursively down the tree.
type
elementtype = record
key: real;
{other fields as warranted}
end;
nodetypes = (leaf, interior);
twothreenode = record
case kind: nodetypes of
leaf: (element: elementtype);
interior: (firstchild, secondchild, thirdchild: ?/FONT> twothreenode;
lowofsecond, lowofthird: real)
end;
SET = ?/FONT> twothreenode;
For convenience, we assume that a 2-3 tree is not a single node or empty. These two cases require a straightforward sequence of steps which the reader is invited to provide as an exercise.
procedure insert1 ( node: ?/FONT> twothreenode;
x: elementtype; { x is to be inserted into the subtree of node }
var pnew: ?/FONT> twothreenode; { pointer to new node
created to right of node }
var low: real ); { smallest element in the subtree pointed to by pnew}
begin
pnew := nil;
if node is a leaf then begin
if x is not the element at node then begin
create new node pointed to by pnew;
put x at the new node;
low := x.key
end
end
else begin { node is an interior node }
let w be the child of node to whose subtree x belongs;
insert1(w, x, pback, lowback);
if pback < > nil then begin
insert pointer pback among the children of node just
to the right of w;
if node has four children then begin
create new node pointed to by pnew;
give the new node the third and fourth children of node;
adjust lowofsecond and lowofthird in node and the new node;
set low to be the lowest key among the
children of the new node
end
end
end
end; { insert 1 }
We would like insert 1 to return both a pointer to a new node, if it must create one, and the key of the smallest element descended from that new node. As the mechanism in Pascal for creating such a function is awkward, we shall instead declare insert 1 to be a procedure that assigns values to parameters pnew and low in the case that it must "return" a new node. We sketch insert 1 in Fig. 5.18. The complete procedure is shown in Fig. 5.19; some comments in Fig. 5.18 have been omitted from Fig. 5.19 to save space.
procedure insert 1 ( node: ?/FONT> twothreenode;
x: elementtype;
var pnew: ?/FONT> twothreenode; var
low: real );
var
pback: ?/FONT> twothreenode;
lowback : real;
child: 1..3; { indicates which child of node is followed
in recursive call (cf. w in Fig. 5.18) }
w: ?/FONT> twothreenode; { pointer to the child }
begin
pnew := nil;
if node ?/FONT>.kind = leaf
then begin
if node ?/FONT>.element.key < >
x .key then begin
{ create new leaf holding x and "return" this node }
new (pnew, leaf);
if (node ?/FONT>.element.key < x.key ) then
{ place x in new node to right of current node }
begin pnew ?/FONT>.element
:= x; low := x .key end
else begin { x belongs to left of element at current node }
pnew ?/FONT>.element := node
?/FONT>.element;
node ?/FONT>.element : = x;
low: =pnew ?/FONT>.element.key
end
end
end
else begin { node is an interior node }
{ select the child of node that we must follow }
if x.key < node ?/FONT>.lowofsecond then
begin child := 1; w := node ?/FONT>.firstchild end
else if (node ?/FONT>.thirdchild
= nil) or (x.key < node ?/FONT>.lowofthird) then begin
{ x is in second subtree }
child := 2;
w := node ?/FONT>.secondchild
end
else begin { x is in third subtree }
child := 3;
w := node ?/FONT>.thirdchild
end;
insert 1 ( w , x, pback, lowback ) ;
if pback < > nil then
{ a new child of node must be inserted }
if node ?/FONT>.thirdchild =
nil then
{ node had only two children, so insert new node in proper place }
if child = 2 then begin
node ?/FONT>.thirdchild :=
pback ;
node ?/FONT>.lowofthird :=
lowback
end
else begin { child = 1 }
node ?/FONT>.thirdchild :=
node ?/FONT>.secondchild ;
node ?/FONT>.lowofthird : =
node ?/FONT>.lowofsecond ;
node ?/FONT>.secondchild :=
pback ;
node ?/FONT>.lowofsecond :=
lowback
end
else begin { node already had three children }
new (pnew , interior );
if child = 3 then begin
{ pback and third child become children of new node }
pnew ?/FONT>.firstchild :=
node ?/FONT>.thirdchild ;
pnew ?/FONT>.secondchild : =
pback ;
pnew ?/FONT>.thirdchild :=
nil;
pnew ?/FONT>.lowofsecond :=
lowback;
{ lowofthird is undefined for pnew}
low := node ?/FONT>.lowofthird ;
node ?/FONT>.thirdchild := nil
end
else begin { child ?/FONT> 2; move third
child of node to pnew}
pnew ?/FONT>.secondchild :=
node ?/FONT>.thirdchild ;
pnew ?/FONT>.lowofsecond :=
node ?/FONT>.lowofthird ;
pnew ?/FONT>.thirdchild : =
nil;
node ?/FONT>.thirdchild := nil
end;
if child = 2 then begin
{ pback becomes first child of pnew}
pnew ?/FONT>.firstchild :=
pback ;
low := lowback
end;
if child = 1 then begin
{ second child of node is moved to pnew;
pback becomes second child of node }
pnew ?/FONT>.firstchild :=
node ?/FONT>.secondchild ;
low := node ?/FONT>.lowofsecond ;
node ?/FONT>.secondchild : =
pback ;
node ?/FONT>.lowofsecond :=
lowback
end
end
end
end; { insert 1 }
Now we can write the procedure INSERT, which calls insert 1. If insert 1 "returns" a new node, then INSERT must create a new root. The code is shown in Fig. 5.20 on the assumption that the type SET is ?/FONT> twothreenode, i.e., a pointer to the root of a 2-3 tree whose leaves contain the members of the set.
procedure INSERT ( x: elementtype; var S: SET );
var
pback: ?/FONT> twothreenode; { pointer to new node
returned by insert 1 }
lowback: real; { low value in subtree of pback }
saveS: SET; { place to store a temporary copy of the pointer S }
begin
{ checks for S being empty or a single node should occur here,
and an appropriate insertion procedure should be included }
insert 1(S, x, pback , lowback ) ;
if pback < > nil then begin
{ create new root; its children are now pointed to by S and pback }
saveS := S;
new(S);
S ?/FONT>.firstchild := saveS;
S ?/FONT>.secondchild := pback;
S ?/FONT>.lowofsecond := lowback;
S ?/FONT>.thirdchild := nil;
end
end; { INSERT }
We shall sketch a function delete 1 that takes a pointer to a node node and an element x, and deletes a leaf descended from node having value x, if there is one.† Function delete 1 returns true if after deletion node has only one child, and it returns false if node still has two or three children. A sketch of the code for delete 1 is shown in Fig. 5.21.
We leave the detailed code for function delete 1 for the reader. Another exercise is to write a procedure DELETE(S, x) that checks for the special cases that the set S consists only of a single leaf or is empty, and otherwise calls delete 1(S, x); if delete 1 returns true, the procedure removes the root (the node pointed to by S) and makes S point to its lone child.
function delete 1 ( node : ?/FONT> twothreenode;
x: elementtype ) : boolean;
var
onlyone: boolean; { to hold the value returned by a call to delete 1 }
begin
delete 1 := false;
if the children of node are leaves then begin
if x is among those leaves then begin
remove x;
shift children of node to the right of x one position left;
if node now has one child then
delete 1 := true
end
end
else begin { node is at level two or higher }
determine which child of node could have x as a descendant;
onlyone := delete 1(w, x); ( w stands for node
?/FONT>.firstchild,
node ?/FONT>.secondchild, or node
?/FONT>.thirdchild, as appropriate }
if onlyone then begin ( fix children of node )
if w is the first child of node then
if y, the second child of node, has three children then
make the first child of y be the second child of w
else begin { y has two children }
make the child of w be the first child of y;
remove w from among the children of node;
if node now has one child then
delete 1 := true
end;
if w is the second child of node then
if y, the first child of node, has three children then
make the third child of y be the first child of w
else { y has two children }
if z, the third child of node, exists
and has three children then
make first child of z be the second child of w
else begin { no other child of node has three children }
make the child of w be the third child of y;
remove w from among the children of node;
if node now has one child then
delete 1 := true
end;
if w is the third child of node then
if y, the second child of node, has three children then
make the third child of y be the first child of w
else begin { y has two children }
make the child of w be the third child of y;
remove w from among the children of node
end { note node surely has two children left in this case }
end
end
end; { delete 1 }
In certain problems we start with a collection of objects, each in a set by itself; we then combine sets in some order, and from time to time ask which set a particular object is in. These problems can be solved using the operations MERGE and FIND. The operation MERGE(A, B, C) makes C equal to the union of sets A and B, provided A and B are disjoint (have no member in common); MERGE is undefined if A and B are not disjoint. FIND(x) is a function that returns the set of which x is a member; in case x is in two or more sets, or in no set, FIND is not defined.
Example 5.6. An equivalence relation is a reflexive, symmetric, and transitive relation. That is, if ?/FONT> is an equivalence relation on set S, then for any (not necessarily distinct) members a, b, and c in S, the following properties hold:
The relation "is equal to" (=) is the paradigm equivalence relation on any set S. For a, b, and c in S, we have (1) a = a, (2) if a = b, then b = a, and (3) if a = b and b = c, then a = c. There are many other equivalence relations, however, and we shall shortly see several additional examples.
In general, whenever we partition a collection of objects into disjoint groups, the relation a ?/FONT> b if and only if a and b are in the same group is an equivalence relation. "Is equal to" is the special case where every element is in a group by itself.
More formally, if a set S has an equivalence relation defined on it, then the set S can be partitioned into disjoint subsets S1, S2, ..., called equivalence classes, whose union is S. Each subset Si consists of equivalent members of S. That is, a ?/FONT> b for all a and b in Si, and a ?? b if a and b are in different subsets. For example, the relation congruence modulo n† is an equivalence relation on the set of integers. To check that this is so, note that a-a = 0, which is a multiple of n (reflexivity); if a-b = dn, then b-a = (-d)n (symmetry); and if a-b = dn and b-c = en, then a-c = (d+e)n (transitivity). In the case of congruence modulo n there are n equivalence classes, which are the set of integers congruent to 0, the set of integers congruent to 1, ... , the set of integers congruent to n - 1.
The equivalence problem can be formulated in the following manner. We are given a set S and a sequence of statements of the form "a is equivalent to b." We are to process the statements in order in such a way that at any time we are able to determine in which equivalence class a given element belongs. For example, suppose S = {1, 2, ... , 7} and we are given the sequence of statements
to process. The following sequence of equivalence classes needs to be constructed, assuming that initially each element of S is in an equivalence class by itself.
1?/FONT>2 {1,2} {3} {4} {5} {6} {7}
5?/FONT>6 {1,2} {3} {4} {5,6} {7}
3?/FONT>4 {1,2} {3,4} {5,6} {7}
1?/FONT>4 {1,2,3,4} {5,6} {7}
We can "solve" the equivalence problem by starting with each element in a named set. When we process statement a?/FONT>b, we FIND the equivalence classes of a and b and then MERGE them. We can at any time use FIND to tell us the current equivalence class of any element.
The equivalence problem arises in several areas of computer science. For example, one form occurs when a Fortran compiler has to process "equivalence declarations" such as
EQUIVALENCE (A(1),B(1,2),C(3)), (A(2),D,E), (F,G)
Another example, presented in Chapter 7, uses solutions to the equivalence problem to help find minimum-cost spanning trees.
Let us begin with a simplified version of the MERGE-FIND ADT. We shall define an ADT, called MFSET, consisting of a set of subsets, which we shall call components, together with the following operations:
To make a reasonable implementation of MFSET, we must restrict our underlying types, or alternatively, we should recognize that MFSET really has two other types as "parameters" - the type of set names and the type of members of these sets. In many applications we can use integers as set names. If we take n to be the number of elements, we may also use integers in the range [1..n] for the members of components. For the implementation we have in mind, it is important that the type of set members be a subrange type, because we want to index into an array defined over that subrange. The type of set names is not important, as this type is the type of array elements, not their indices. Observe, however, that if we wanted the member type to be other than a subrange type, we could create a mapping, with a hash table, for example, that assigned these to unique integers in a subrange. We only need to know the total number of elements in advance.
The implementation we have in mind is to declare
const
n = { number of elements };
type
MFSET = array[1..n] of integer;
as a special case of the more general type
array[subrange of members] of (type of set names);
Suppose we declare components to be of type MFSET with the intention that components[x] holds the name of the set currently containing x. Then the three MFSET operations are easy to write. For example, the operation MERGE is shown in Fig. 5.22. INITIAL(A, x) simply sets components[x] to A, and FIND(x) returns components [x].
The time performance of this implementation of MFSET is easy to
procedure MERGE ( A, B: integer; var C: MFSET );
var
x: 1..n;
begin
for x:= 1 to n do
if C[x] = B then
C[x] := A
end; { MERGE }
Fig. 5.22. The procedure MERGE.
analyze. Each execution of the procedure MERGE takes O(n) time. On the other hand, the obvious implementations of INITIAL(A, x) and FIND(x) have constant running times.Using the algorithm in Fig. 5.22, a sequence of n-1 MERGE instructions
will take O(n2) time.†
One way to speed up the MERGE operation is to link
together all members of a component in a list. Then, instead of scanning all
members when we merge component B into A, we need only run down the list
of members of B. This arrangement saves time on the average. However, it
could happen that the ith merge is of the form MERGE(A, B) where
A is a
component of size 1 and B is a component of size i, and that the result is
named A. This merge operation would require O(i) steps, and a sequence of
n-1 such merge instructions would take on the order of
 time.
time.
One way to avoid this worst case situation is to keep track of the size of each component and always merge the smaller into the larger.‡ Thus, every time a member is merged into a bigger component, it finds itself in a component at least twice as big. Thus, if there are initially n components, each with one member, none of the n members can have its component changed more than 1+log n times. As the time spent by this new version of MERGE is proportional to the number of members whose component names are changed, and the total number of such changes is at most n(1+log n), we see that O(n log n) work suffices for all merges.
Now let us consider the data structure needed for this implementation. First, we need a mapping from set names to records consisting of
We also need another array of records, indexed by members, to indicate
We use 0 to serve as NIL, the end-of-list marker. In a language that lent itself to such constructs, we would prefer to use pointers in this array, but Pascal does not permit pointers into arrays.
In the special case where set names, as well as members, are chosen from the subrange 1..n, we can use an array for the mapping described above. That is, we define
type
nametype: 1..n;
elementtype = 1..n;
MFSET = record
setheaders: array[ 1..n] of record
{ headers for set lists }
count: 0..n;
firstelement: 0..n
end;
names; array[1..n] of record
{ table giving set containing each member }
setname: nametype;
nextelement: 0..n
end
end;
The procedures INITIAL, MERGE, and FIND are shown in Fig. 5.23.
Figure 5.24 shows an example of the data structure used in Fig. 5.23, where set 1 is {1, 3, 4}, set 2 is {2}, and set 5 is {5, 6}.
Another, completely different, approach to the implementation of MFSET's uses trees with pointers to parents. We shall describe this approach informally. The basic idea is that nodes of trees correspond to set members, with an array or other implementation of a mapping leading from set members to their nodes. Each node, except the root of each tree, has a pointer to its parent. The roots hold the name of the set, as well as an element. A mapping from set names to roots allows access to any given set, when merges are done.
Figure 5.25 shows the sets A = {1, 2, 3, 4}, B = {5, 6}, and C = {7} represented in this form. The rectangles are assumed to be part of the root node, not separate nodes.
procedure INITIAL ( A: nametype; x: elementtype; var C:
MFSET );
{ initialize A to a set containing x only }
begin
C.names [x].setname : = A;
C.names [x].nextelement := 0;
{ null pointer at end of list of members of A }
C.setheaders [A].count := 1;
C.setheaders [A].firstelement := x
end; { INITIAL }
procedure MERGE ( A, B: nametype; var C: MFSET );
{ merge A and B, calling the result A or B, arbitrarily }
var
i: 0..n; { used to find end of smaller list }
begin
if C.setheaders [A ].count > C.setheaders
[B].count then begin
{ A is the larger set; merge B into A }
{ find end of B, changing set names to A as we go }
i := C.setheaders[B].firstelement;
while C.names [i].nextelement <> 0 do
begin
C.names [i].setname := A;
i := C.names [i].nextelement
end;
{ append list A to the end of B and call the result A }
{ now i is the index of the last member of B }
C.names [i].setname := A;
C.names [i].nextelement := C.setheaders [A
].firstelement;
C.setheaders [A ].firstelement := C.setheaders [B
].firstelement;
C.setheaders [A ].count := C.setheaders [A
].count +
C.setheaders [B ].count;
C.setheaders[B ].count := 0;
C.setheaders[B ].firstelement := 0
{ above two steps not really necessary, as set B no longer exists }
end
else { B is at least as large as A }
{ code similar to case above, but with A and B interchanged }
end; { MERGE }
function FIND ( x: 1..n; var C: MFSET );
{ return the name of the set of which x is a member }
begin
return ( C. names [x ].setname)
end; { FIND }
Fig. 5.23. The operations of an MFSET.
To find the set containing an element x, we first consult a mapping (e.g., an array) not shown in Fig. 5.25, to obtain a pointer to the node for x. We then follow the path from that node to the root of its tree and read the name of the set there.
The basic merge operation is to make the root of one tree be a child of the root of the other. For example, we could merge A and B of Fig. 5.25 and call the result A, by making node 5 a child of node 1. The result is shown in Fig. 5.26. However, indiscriminate merging could result in a tree of n nodes that is a single chain. Then doing a FIND operation on each of those nodes would take O(n2) time. Observe that although a merge can be done in O(1) steps, the cost of a reasonable number of FIND's will dominate the total cost, and this approach is not necessarily better than the simplest one for executing n merges and n finds.
However, a simple improvement guarantees that if n is the number of elements, then no FIND will take more than O(log n) steps. We simply keep at each root a count of the number of elements in the set, and when called upon to merge two sets, we make the root of the smaller tree be a child of the root of the larger. Thus, every time a node is moved to a new tree, two things happen: the distance from the node to its root increases by one, and the node will be in a set with at least twice as many elements as before. Thus, if n is the total number of elements, no node can be moved more than logn times; hence, the distance to its root can never exceed logn. We conclude that each FIND requires at most O(log n) time.
Another idea that may speed up this implementation of MFSET's is path compression. During a FIND, when following a path from some node to the root, make each node encountered along the path be a child of the root. The easiest way to do this is in two passes. First, find the root, and then retraverse the same path, making each node a child of the root.
Example 5.7. Figure 5.27(a) shows a tree before executing a FIND operation on the node for element 7 and Fig. 5.27(b) shows the result after 5 and 7 are made children of the root. Nodes 1 and 2 on the path are not moved because 1 is the root, and 2 is already a child of the root.
Path compression does not affect the cost of MERGE's; each MERGE still takes a constant amount of time. There is, however, a subtle speedup in FIND's since path compression tends to shorten a large number of paths from various nodes to the root with relatively little effort.
Unfortunately, it is very difficult to analyze the average cost of FIND's when path compression is used. It turns out that if we do not require that smaller trees be merged into larger ones, we require no more than O(n log n) time to do n FIND's. Of course, the first FIND may take O(n) time by itself for a tree consisting of one chain. But path compression can change a tree very rapidly and no matter in what order we apply FIND to elements of any tree no more than O(n) time is spent on n FIND's. However, there are
Fig. 5.24. Example of the MFSET data structure.
Fig. 5.25. MFSET represented by a collection of trees.
sequences of MERGE and FIND instructions that require W(nlog n) time.The algorithm that both uses path compression and merges the smaller tree into the larger is asymptotically the most efficient method known for implementing MFSET's. In particular, n FIND's require no more than O(na(n)) time, where a(n) is a function that is not constant, yet grows much more slowly than logn. We shall define a(n) below, but the analysis that leads to this bound is beyond the scope of this book.
Fig. 5.26. Merging B into A.
Fig. 5.27. An example of path compression.
The function a(n) is closely related to a very rapidly growing function A(x, y), known as Ackermann's function. A(x, y) is defined recursively by:
A(0,y) = 1 for y ?/FONT> 0
A(1, 0) = 2
A(x, 0) = x+2 for x ?/FONT> 2
A(x,y) = A(A(x-1, y),y-1) for x, y ?/FONT> 1
Each value of y defines a function of one variable. For example, the third line above tells us that for y=0, this function is "add 2." For y = 1, we have A(x, 1) = A(A(x-1, 1),0) = A(x-1, 1) + 2, for x > 1, with A(1, 1) = A(A(0, 1),0) = A(1, 0) = 2. Thus A(x, 1) = 2x for all x ?/FONT> 1. In other words, A(x, 1) is "multiply by 2." Then, A(x, 2) = A(A(x-1, 2), 1) = 2A(x-1, 2) for x > 1. Also, A(1, 2) = A(A(0,2), 1) = A(1, 1) = 2. Thus A(x, 2) = 2x. Similarly, we can show that A(x, 3) = 22...2 (stack of x 2's), while A(x, 4) is so rapidly growing there is no accepted mathematical notation for such a function.
A single-variable Ackermann's function can be defined by letting A(x) = A(x, x). The function a(n) is a pseudo-inverse of this single variable function. That is, a(n) is the least x such that n ?/FONT> A(x). For example, A(1) = 2, so a(1) = a(2) = 1. A(2) = 4, so a(3) = a(4) = 2. A(3) = 8, so a(5) = . . . = a(8) = 3. So far, a(n) seems to be growing rather steadily.
However, A(4) is a stack of 65536 2's. Since log(A(4)) is a stack of 65535 2's, we cannot hope even to write A(4) explicitly, as it would take log(A(4)) bits to do so. Thus a(n) ?/FONT> 4 for all integers n one is ever likely to encounter. Nevertheless, a(n) eventually reaches 5, 6, 7, . . . on its unimaginably slow course toward infinity.
A subsequence of a sequence x is obtained by removing zero or more (not necessarily contiguous) elements from x. Given two sequences x and y, a longest common subsequence (LCS) is a longest sequence that is a subsequence of both x and y.
For example, an LCS of 1, 2, 3, 2, 4, 1, 2 and 2, 4, 3, 1, 2, 1 is the subsequence 2, 3, 2, 1, formed as shown in Fig. 5.28. There are other LCS's as well, such as 2, 4, 1, 2, but there are no common subsequences of length 5.
Fig. 5.28. A longest common subsequence.
There is a UNIX command called diff that compares files line-by-line, finding a longest common subsequence, where a line of a file is considered an element of the subsequence. That is, whole lines are analogous to the integers 1, 2, 3, and 4 in Fig. 5.28. The assumption behind the command diff is that the lines of each file that are not in this LCS are lines inserted, deleted or modified in going from one file to the other. For example, if the two files are versions of the same program made several days apart, diff will, with high probability, find the changes.
There are several general solutions to the LCS problem that work in O(n2) steps on sequences of length n. The command diff uses a different strategy that works well when the files do not have too many repetitions of any line. For example, programs will tend to have lines "begin" and "end" repeated many times, but other lines are not likely to repeat.
The algorithm used by diff for finding an LCS makes use of an efficient implementation of sets with operations MERGE and SPLIT, to work in time O(plogn), where n is the maximum number of lines in a file and p is the number of pairs of positions, one from each file, that have the same line. For example, p for the strings in Fig. 5.28 is 12. The two 1's in each string contribute four pairs, the 2's contribute six pairs, and 3 and 4 contribute one pair each. In the worst case, p,. could be n2, and this algorithm would take O(n2logn) time. However, in practice, p is usually closer to n, so we can expect an O(nlogn) time complexity.
To begin the description of the algorithm let A = a1a2 ???/FONT> an and B = b1b2 ?? ?/FONT> bm be the two strings whose LCS we desire. The first step is to tabulate for each value a, the positions of the string A at which a appears. That is, we define PLACES(a)= { i ?/FONT> a = ai }. We can compute the sets PLACES(a) by constructing a mapping from symbols to headers of lists of positions. By using a hash table, we can create the sets PLACES(a) in O(n) "steps" on the average, where a "step" is the time it takes to operate on a symbol, say to hash it or compare it with another. This time could be a constant if symbols are characters or integers, say. However, if the symbols of A and B are really lines of text, then steps take an amount of time that depends on the average length of a line of text.
Having computed PLACES(a) for each symbol a that occurs in string A, we are ready to find an LCS. To simplify matters, we shall only show how to find the length of the LCS, leaving the actual construction of the LCS as an exercise. The algorithm considers each bj, for j = 1, 2, ... , m, in turn. After considering bj, we need to know, for each i between 0 and n, the length of the LCS of strings a1 ???/FONT> ai and b1 ???/FONT> bj.
We shall group values of i into sets Sk, for k = 0, 1, . . . , n, where Sk consists of all those integers i such that the LCS of a1 ???/FONT> ai and b1 ???/FONT> bj has length k. Note that Sk will always be a set of consecutive integers, and the integers in Sk+1 are larger than those in Sk, for all k.
Example 5.8. Consider Fig. 5.28, with j = 5. If we try to match zero symbols from the first string with the first five symbols of the second (24312), we naturally have an LCS of length 0, so 0 is in S0. If we use the first symbol from the first string, we can obtain an LCS of length 1, and if we use the first two symbols, 12, we can obtain an LCS of length 2. However, using 123, the first three symbols, still gives us an LCS of length 2 when matched against 24312. Proceeding in this manner, we discover S0 = {0}, S1 = {1}, S2 = {2, 3}, S3 = {4, 5, 6}, and S4 = {7}.
Suppose that we have computed the Sk's for position j-1 of the second string and we wish to modify them to apply to position j. We consider the set PLACES(bj). For each r in PLACES(bj), we consider whether we can improve some of the LCS's by adding the match between ar and bj to the LCS of a1 ???/FONT> ar- 1 and b1 ???/FONT> bj. That is, if both r-1 and r are in Sk, then all s ?/FONT> r in Sk really belong in Sk+1 when bj is considered. To see this we observe that we can obtain k matches between a1 ???/FONT> ar-1 and bl ?? ?/FONT> bj-1, to which we add a match between ar and bj. We can modify Sk and Sk+1 by the following steps.
It is important to consider the members of PLACES(bj) largest first. To see why, suppose for example that 7 and 9 are in PLACES(bj), and before bj is considered, S3={6, 7, 8, 9} and S4={10, 11}.
If we consider 7 before 9, we split S3 into S3 = {6} and S'3 = {7, 8, 9}, then make S4 = {7, 8, 9, 10, 11}. If we then consider 9, we split S4 into S4={7, 8} and S'4 = {9, 10, 11}, then merge 9, 10 and 11 into S5. We have thus moved 9 from S3 to S5 by considering only one more position in the second string, representing an impossibility. Intuitively, what has happened is that we have erroneously matched bj against both a7 and a9 in creating an imaginary LCS of length 5.
In Fig. 5.29, we see a sketch of the algorithm that maintains the sets Sk as we scan the second string. To determine the length of an LCS, we need only execute FIND(n) at the end.
procedure LCS;
begin
(1) initialize S0 = {0, 1, ... , n} and Si = ?/FONT> for i = 1, 2, ... , n;
(2) for j := 1 to n do { compute Sk's for position
j }
(3) for r in PLACES(bj), largest first do begin
(4) k := FIND(r);
(5) if k = FIND(r-1) then begin { r is not
smallest in Sk }
(6) SPLIT(Sk, Sk, S'k,
r);
(7) MERGE(S'k, Sk+1,
Sk+1)
end
end
end; { LCS }
Fig. 5.29. Sketch of longest common subsequence program.
As we mentioned earlier, the algorithm of Fig. 5.29 is a useful approach only if there are not too many matches between symbols of the two strings. The measure of the number of matches is

where |PLACES(bj)| denotes the number of elements in set PLACES(bj). In other words, p is the sum over all bj of the number of positions in the first string that match bj. Recall that in our discussion of file comparison, we expect p to be of the same order as m and n, the lengths of the two strings (files).
It turns out that the 2-3 tree is a good structure for the sets Sk. We can initialize these sets, as in line (1) of Fig. 5.29, in O(n) steps. The FIND operation requires an array to serve as a mapping from positions r to the leaf for r and also requires pointers to parents in the 2-3 tree. The name of the set, i.e., k for Sk, can be kept at the root, so we can execute FIND in O(logn) steps by following parent pointers until we reach the root. Thus all executions of lines (4) and (5) together take O(plogn) time, since those lines are each executed exactly once for each match found.
The MERGE operation of line (5) has the special property that every member of S'k is lower than every member of Sk+1, and we can take advantage of this fact when using 2-3 trees for an implementation.† To begin the MERGE, place the 2-3 tree for S'k to the left of that for Sk+1. If both are of the same height, create a new root with the roots of the two trees as children. If S'k is shorter, insert the root of that tree as the leftmost child of the leftmost node of Sk+1 at the appropriate level. If this node now has four children, we modify the tree exactly as in the INSERT procedure of Fig. 5.20. An example is shown in Fig. 5.30. Similarly, if Sk+1 is shorter, make its root the rightmost child of the rightmost node of S'k at the appropriate level.
Fig. 5.30. Example of MERGE.
The SPLIT operation at r requires that we travel up the tree from leaf r, duplicating every interior node along the path and giving one copy to each of the two resulting trees. Nodes with no children are eliminated, and nodes with one child are removed and have that child inserted into the proper tree at the proper level.
Example 5.9. Suppose we split the tree of Fig. 5.30(b) at node 9. The two trees, with duplicated nodes, are shown in Fig. 5.31(a). On the left, the parent of 8 has only one child, so 8 becomes a child of the parent of 6 and 7. This parent now has three children, so all is as it should be; if it had four children, a new node would have been created and inserted into the tree. We need only eliminate nodes with zero children (the old parent of 8) and the chain of nodes with one child leading to the root. The parent of 6, 7, and 8 becomes the new root, as shown in Fig. 5.31(b). Similarly, in the right-hand tree, 9 becomes a sibling of 10 and 11, and unnecessary nodes are eliminated, as is also shown in Fig. 5.31(b).
Fig. 5.31. An example of SPLIT.
If we do the splitting and reorganization of the 2-3 tree bottom up, it can be shown by consideration of a large number of cases that O(logn) steps suffices. Thus, the total time spent in lines (6) and (7) of Fig. 5.29 is O(plogn), and hence the entire algorithm takes O(plogn) steps. We must add in the preprocessing time needed to compute and sort PLACES(a) for symbols a. As we mentioned, if the symbols a are "large" objects, this time can be much greater than any other part of the algorithm. As we shall see in Chapter 8, if the symbols can be manipulated and compared in single "steps," then O(nlogn) time suffices to sort the first string a1a2 ???/FONT> an (actually, to sort objects (i, ai) on the second field), whereupon PLACES(a) can be read off from this list in O(n) time. Thus, the length of the LCS can be computed in O(max(n, p) logn) time which, since p ?/FONT> n is normal, can be taken as O(plogn).
| 5.1 | Draw all possible binary search trees containing the four elements 1, 2, 3, 4. |
|---|---|
| 5.2 | Insert the integers 7, 2, 9, 0, 5, 6, 8, 1 into a binary search tree by repeated application of the procedure INSERT of Fig. 5.3. |
| 5.3 | Show the result of deleting 7, then 2 from the final tree of Exercise 5.2. |
| *5.4 | When deleting two elements from a binary search tree using the procedure of Fig. 5.5, does the final tree ever depend on the order in which you delete them? |
| 5.5 | We wish to keep track of all 5-character substrings that occur in a given string, using a trie. Show the trie that results when we insert the 14 substrings of length five of the string ABCDABACDEBACADEBA. |
| *5.6 | To implement Exercise 5.5, we could keep a pointer at each leaf, which, say, represents string abcde, to the interior node representing the suffix bcde. That way, if the next symbol, say f, is received, we don't have to insert all of bcdef, starting at the root. Furthermore, having seen abcde, we may as well create nodes for bcde, cde, de, and e, since we shall, unless the sequence ends abruptly, need those nodes eventually. Modify the trie data structure to maintain such pointers, and modify the trie insertion algorithm to take advantage of this data structure. |
| 5.7 | Show the 2-3 tree that results if we insert into an empty set, represented as a 2-3 tree, the elements 5, 2, 7, 0, 3, 4, 6, 1, 8, 9. |
| 5.8 | Show the result of deleting 3 from the 2-3 tree that results from Exercise 5.7. |
| 5.9 | Show the successive values of the various Si's when implementing the LCS algorithm of Fig. 5.29 with first string abacabada, and second string bdbacbad. |
| 5.10 | Suppose we use 2-3 trees to implement the MERGE and SPLIT
operations as in Section 5.6.
|
| 5.11 | Some of the structures discussed in this chapter can be modified easily
to support the MAPPING ADT. Write procedures MAKENULL,
ASSIGN, and COMPUTE to operate on the following data structures.
|
| 5.12 | Show that in any subtree of a binary search tree, the minimum element is at a node without a left child. |
| 5.13 | Use Exercise 5.12 to produce a nonrecursive version of DELETE-MIN. |
| 5.14 | Write procedures ASSIGN, VALUEOF, MAKENULL and GETNEW for trie nodes represented as lists of cells. |
| *5.15 | How do the trie (list of cells implementation), the open hash table, and the binary search tree compare for speed and for space utilization when elements are strings of up to ten characters? |
| *5.16 | If elements of a set are ordered by a "<" relation, then we can keep one or two elements (not just their keys) at interior nodes of a 2-3 tree, and we then do not have to keep these elements at the leaves. Write INSERT and DELETE procedures for 2-3 trees of this type. |
| 5.17 | Another modification we could make to 2-3 trees is to keep only keys
at interior nodes, but do not require that the keys k1 and k2
at a node
truly be the minimum keys of the second and third subtrees, just that
all keys k of the third subtree satisfy k ?/FONT>
k2, all keys k of the second
satisfy k1 ?/FONT> k <
k2, and all keys k of the first satisfy k < k1.
|
| *5.18 | Another data structure that supports dictionaries with the MIN operation is the AVL tree (named for the inventors' initials) or height-balanced tree. These trees are binary search trees in which the heights of two siblings are not permitted to differ by more than one. Write procedures to implement INSERT and DELETE, while maintaining the AVL-tree property. |
| 5.19 | Write the Pascal program for procedure delete1 of Fig. 5.21. |
| *5.20 | A finite automaton consists of a set of states, which we shall take to be the integers 1..n and a table transitions[state, input] giving a next state for each state and each input character. For our purposes, we shall assume that the input is always either 0 or 1. Further, certain of the states are designated accepting states. For our purposes, we shall assume that all and only the even numbered states are accepting. Two states p and q are equivalent if either they are the same state, or (i) they are both accepting or both nonaccepting, (ii) on input 0 they transfer to equivalent states, and (iii) on input 1 they transfer to equivalent states. Intuitively, equivalent states behave the same on all sequences of inputs; either both or neither lead to accepting states. Write a program using the MFSET operations that computes the sets of equivalent states of a given finite automaton. |
| **5.21 | In the tree implementation of MFSET:
|
| 5.22 | Select a data structure and write a program to compute PLACES (defined in Section 5.6) in average time O(n) for strings of length n. |
| *5.23 | Modify the LCS procedure of Fig. 5.29 to compute the LCS, not just its length. |
| *5.24 | Write a detailed SPLIT procedure to work on 2-3 trees. |
| *5.25 | If elements of a set represented by a 2-3 tree consist only of a key field, an element whose key appears at an interior node need not appear at a leaf. Rewrite the dictionary operations to take advantage of this fact and avoid storing any element at two different nodes. |
Tries were first proposed by Fredkin [1960]. Bayer and McCreight [1972] introduced B-trees, which, as we shall see in Chapter 11, are a generalization of 2-3 trees. The first uses of 2-3 trees were by J. E. Hopcroft in 1970 (unpublished) for insertion, deletion, concatenation, and splitting, and by Ullman [1974] for a code optimization problem.
The tree structure of Section 5.5, using path compression and merging smaller into larger, was first used by M. D. McIlroy and R. Morris to construct minimum-cost spanning trees. The performance of the tree implementation of MFSET's was analyzed by Fischer [1972] and by Hopcroft and Ullman [1973]. Exercise 5.21(b) is from Tarjan [1975].
The solution to the LCS problem of Section 5.6 is from Hunt and Szymanski [1977]. An efficient data structure for FIND, SPLIT, and the restricted MERGE (where all elements of one set are less than those of the other) is described in van Emde Boas, Kaas, and Zijlstra [1977].
Exercise 5.6 is based on an efficient algorithm for matching patterns developed by Weiner [1973]. The 2-3 tree variant of Exercise 5.16 is discussed in detail in Wirth [1976]. The AVL tree structure in Exercise 5.18 is from Adel'son-Vel'skii and Landis [1962].
† Recall the left child of the root is a descendant of itself, so we have not ruled out the possibility that x is at the left child of the root.
† The highest-valued node among the descendants of the left child would do as well.
† Recall that all logarithms are to the base 2 unless otherwise noted.
† Trie was originally intended to be a homonym of "tree" but to distinguish these two terms many people prefer to pronounce trie as though it rhymes with "pie."
† VALUEOF is a function version of COMPUTE in Section 2.5.
† There is another version of 2-3 trees that places whole records at interior nodes, as a binary search tree does.
† All nodes, however, take the largest amount of space needed for any variant types, so Pascal is not really the best language of implementing 2-3 trees in practice.M
† A useful variant would take only a key value and delete any element with that key.
† We say a is congruent to b modulo n if a and b have the same remainders when divided by n, or put another way, a-b is a multiple of n.
† Note that n- 1 is the largest number of merges that can be performed before all elements are in one set.
‡ Note that our ability to call the resulting component by the name of either of its constituents is important here, although in the simpler implementation, the name of the first argument was always picked.
† Strictly speaking we should use a different name for the MERGE operation, as the implementation we propose will not work to compute the arbitrary union of disjoint sets, while keeping the elements sorted so operations like SPLIT and FIND can be performed.