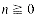 elements. The ai are referred to as atoms which are taken from some set. The null or empty list has n = 0 elements.
elements. The ai are referred to as atoms which are taken from some set. The null or empty list has n = 0 elements.
A stack is an ordered list in which all insertions and deletions are made at one end, called the top. A queue is an ordered list in which all insertions take place at one end, the rear, while all deletions take place at the other end, the front. Given a stack S = (a1, ...an) then we say that a1 is the bottommost element and element ai is on top of element ai - 1, 1 < i  n. When viewed as a queue with an as the rear element one says that ai+1 is behind ai, 1
n. When viewed as a queue with an as the rear element one says that ai+1 is behind ai, 1  i< n.
i< n.
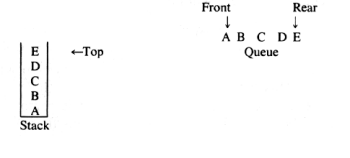
Figure 3.1
The restrictions on a stack imply that if the elements A,B,C,D,E are added to the stack, in that order, then the first element to be removed/deleted must be E. Equivalently we say that the last"element to be inserted into the stack will be the first to be removed. For this reason stacks are sometimes referred to as Last In First Out (LIFO) lists. The restrictions on a queue require that the first element which is inserted into the queue will be the first one to be removed. Thus A is the first letter to be removed, and queues are known as First In First Out (FIFO) lists. Note that the data object queue as defined here need not necessarily correspond to the mathematical concept of queue in which the insert/delete ru les may be different.
One natural example of stacks which arises in computer programming is the processing of subroutine calls and their returns. Suppose we have a main procedure and three subroutines as below:
| proc MAIN | | proc A1 | | proc A2 | | proc A3 |
| ___ | | ___ | | ___ | | ___ |
| ___ | | ___ | | ___ | | ___ |
| ___ | | ___ | | ___ | | ___ |
| call A1 | | call A2 | | call A3 | | ___ |
| r: | | s: | | t: | | |
| ___ | | ___ | | ___ | | ___ |
| ___ | | ___ | | ___ | | ___ |
| end | | end | | end | | end |
Figure 3.2. Sequence of subroutine calls
The MAIN program calls subroutine A1. On completion of A1 execution of MAIN will resume at location r. The address r is passed to Al which saves it in some location for later processing. Al then invokes A2 which in turn calls A3. In each case the calling procedure passes the return address to the called procedure. If we examine the memory while A3 is computing there will be an implicit stack which looks like
(q,r,s,t).
The first entry, q, is the address in the operating system where MAIN returns control. This list operates as a stack since the returns will be made in the reverse order of the calls. Thus t is removed before s, s before r and r before q. Equivalently, this means that A3 must finish processing before A2, A2 before A1, and A1 before MAIN. This list of return addresses need not be maintained in consecutive locations. For each subroutine there is usually a single location associated with the machine code which is used to retain the return address. This can be severely limiting in the case of recursive calls and re-entrant routines, since every time we call a subroutine the new return address wipes out the old one. For example, if we inserted a call to A1 within subroutine A3 expecting the return to be at location u, then at execution time the stack would become (q,u,s,t) and the return address r would be lost. When recursion is allowed, it is no longer adequate to reserve one location for the return address of each subroutine. Since returns are made in the reverse order of calls, an elegant and natural solution to this subroutine return problem is afforded through the explicit use of a stack of return addresses. Whenever a return is made, it is to the top address in the stack. Implementing recursion using a stack is discussed in Section 4.10.
Associated with the object stack there are several operations that are necessary:
CREATE (S) which creates S as an empty stack;
ADD (i,S) which inserts the element i onto the stack S and returns the new stack;
DELETE (S) which removes the top element of stack S and returns the new stack;
TOP (S) which returns the top element of stack S;
ISEMTS (S) which returns true if S is empty else false;
These five functions constitute a working definition of a stack. However we choose to represent a stack, it must be possible to build these operations. But before we do this let us describe formally the structure STACK.
The five functions with their domains and ranges are declared in lines 1 through 5. Lines 6 through 13 are the set of axioms which describe how the functions are related. Lines 10 and 12 are the essential ones which define the last-in-first-out behavior. The above definitions describe an infinite stack for no upper bound on the number of elements is specified. This will be dealt with when we represent this structure in a computer.
The simplest way to represent a stack is by using a one-dimensional array, say STACK(1:n), where n is the maximum number of allowable entries. The first or bottom element in the stack will be stored at STACK(1), the second at STACK(2) and the i-th at STACK(i). Associated with the array will be a variable, top, which points to the top element in the stack. With this decision made the following implementations result:
The implementations of these three operations using an array are so short that we needn't make them separate procedures but can just use them directly whenever we need to. The ADD and DELETE operations are only a bit more complex.
These two procedures are so simple that they perhaps need no more explanation. Procedure DELETE actually combines the functions TOP and DELETE. STACK_FULL and STACK_EMPTY are procedures which we leave unspecified since they will depend upon the particular application. Often a stack full condition will signal that more storage needs to be allocated and the program re-run. Stack empty is often a meaningful condition. In Section 3.3 we will see a very important computer application of stacks where stack empty signals the end of processing.
The correctness of the stack implementation above may be established by showing that in this implementation, the stack axioms of lines 7-12 of the stack structure definition are true. Let us show this for the first three rules. The remainder of the axioms can be shown to hold similarly .
(i) line 7: ISEMTS(CREATE):: = true
Since CREATE results in top being initialized to zero, it follows from the implementation of ISEMTS that ISEMTS(CREATE):: = true.
(ii) line 8: ISEMTS(ADD(i,S)):: = false
The value of top is changed only in procedures CREATE, ADD and DELETE. CREATE initializes top to zero while ADD increments it by 1 so long as top is less than n (this is necessary because we can implement only a finite stack). DELETE decreases top by 1 but never allows its value to become less than zero. Hence, ADD(i,S) either results in an error condition (STACK_FULL), or leaves the value of top > 0. This then implies that ISEMTS(ADD(i,S)):: = false.
(iii) line 9: DELETE(CREATE):: = error
This follows from the observation that CREATE sets top = 0 and the procedure DELETE signals the error condition STACK_EMPTY when top = 0.
Queues, like stacks, also arise quite naturally in the computer solution of many problems. Perhaps the most common occurrence of a queue in computer applications is for the scheduling of jobs. In batch processing the jobs are ''queued-up'' as they are read-in and executed, one after another in the order they were received. This ignores the possible existence of priorities, in which case there will be one queue for each priority.
As mentioned earlier, when we talk of queues we talk about two distinct ends: the front and the rear. Additions to the queue take place at the rear. Deletions are made from the front. So, if a job is submitted for execution, it joins at the rear of the job queue. The job at the front of the queue is the next one to be executed. A minimal set of useful operations on a queue includes the following:
CREATEQ(Q) which creates Q as an empty queue;
ADDQ(i,Q) which adds the element i to the rear of a queue and returns the new queue;
DELETEQ(Q) which removes the front element from the queue Q and returns the resulting queue;
FRONT(Q) which returns the front element of Q;
ISEMTQ(Q) which returns true if Q is empty else false.
A complete specification of this data structure is
The axiom of lines 10-12 shows that deletions are made from the front of the queue.
The representation of a finite queue in sequential locations is somewhat more difficult than a stack. In addition to a one dimensional array Q(1:n), we need two variables, front and rear. The conventions we shall adopt for these two variables are that front is always 1 less than the actual front of the queue and rear always points to the last element in the queue. Thus, front = rear if and only if there are no elements in the queue. The initial condition then is front = rear = 0. With these conventions, let us try an example by inserting and deleting jobs, Ji,from a job queue
With this scheme, the following implementation of the CREATEQ, ISEMTQ, and FRONT operations results for a queue with capacity n:
The following algorithms for ADDQ and DELETEQ result:
The correctness of this implementation may be established in a manner akin to that used for stacks. With this set up, notice that unless the front regularly catches up with the rear and both pointers are reset to zero, then the QUEUE_FULL signal does not necessarily imply that there are n elements in the queue. That is, the queue will gradually move to the right. One obvious thing to do when QUEUE_FULL is signaled is to move the entire queue to the left so that the first element is again at Q(1) and front = 0. This is time consuming, especially when there are many elements in the queue at the time of the QUEUE_FULL signal.
Let us look at an example which shows what could happen, in the worst case, if each time the queue becomes full we choose to move the entire queue left so that it starts at Q(1). To begin, assume there are n elements J1, ...,Jn in the queue and we next receive alternate requests to delete and add elements. Each time a new element is added, the entire queue of n - 1 elements is moved left.
A more efficient queue representation is obtained by regarding the array Q(1:n) as circular. It now becomes more convenient to declare the array as Q(0:n - 1). When rear = n - 1, the next element is entered at Q(0) in case that spot is free. Using the same conventions as before, front will always point one position counterclockwise from the first element in the queue. Again, front = rear if and only if the queue is empty. Initially we have front = rear = 1. Figure 3.4 illustrates some of the possible configurations for a circular queue containing the four elements J1-J4 with n > 4. The assumption of circularity changes the ADD and DELETE algorithms slightly. In order to add an element, it will be necessary to move rear one position clockwise, i.e.,
Using the modulo operator which computes remainders, this is just rear
One surprising point in the two algorithms is that the test for queue full in ADDQ and the test for queue empty in DELETEQ are the same. In the case of ADDQ, however, when front = rear there is actually one space free, i.e. Q(rear), since the first element in the queue is not at Q(front) but is one position clockwise from this point. However, if we insert an item here, then we will not be able to distinguish between the cases full and empty, since this insertion would leave front = rear. To avoid this, we signal queue-full thus permitting a maximum, of n - 1 rather than n elements to be in the queue at any time. One way to use all n positions would be to use another variable, tag, to distinguish between the two situations, i.e. tag = 0 if and only if the queue is empty. This would however slow down the two algorithms. Since the ADDQ and DELETEQ algorithms will be used many times in any problem involving queues, the loss of one queue position will be more than made up for by the reduction in computing time.
The procedures QUEUE_FULL and QUEUE_EMPTY have been used without explanation, but they are similar to STACK_FULL and STACK_EMPTY. Their function will depend on the particular application.
The rat-in-a-maze experiment is a classical one from experimental psychology. A rat (or mouse) is placed through the door of a large box without a top. Walls are set up so that movements in most directions are obstructed. The rat is carefully observed by several scientists as it makes its way through the maze until it eventually reaches the other exit. There is only one way out, but at the end is a nice hunk of cheese. The idea is to run the experiment repeatedly until the rat will zip through the maze without taking a single false path. The trials yield his learning curve.
We can write a computer program for getting through a maze and it will probably not be any smarter than the rat on its first try through. It may take many false paths before finding the right one. But the computer can remember the correct path far better than the rat. On its second try it should be able to go right to the end with no false paths taken, so there is no sense re-running the program. Why don't you sit down and try to write this program yourself before you read on and look at our solution. Keep track of how many times you have to go back and correct something. This may give you an idea of your own learning curve as we re-run the experiment throughout the book.
Let us represent the maze by a two dimensional array, MAZE(1:m, 1:n), where a value of 1 implies a blocked path, while a 0 means one can walk right on through. We assume that the rat starts at MAZE(1,1) and the exit is at MAZE(m,n).
With the maze represented as a two dimensional array, the location of the rat in the maze can at any time be described by the row, i, and column, j of its position. Now let us consider the possible moves the rat can make at some point (i,j) in the maze. Figure 3.6 shows the possible moves from any point (i,j). The position (i,j) is marked by an X. If all the surrounding squares have a 0 then the rat can choose any of these eight squares as its next position. We call these eight directions by the names of the points on a compass north, northeast, east, southeast, south, southwest, west, and northwest, or N, NE, E, SE, S, SW, W, NW.
We must be careful here because not every position has eight neighbors. If (i,j) is on a border where either i = 1 or m, or j = 1 or n, then less than eight and possibly only three neighbors exist. To avoid checking for these border conditions we can surround the maze by a border of ones. The array will therefore be declared as MAZE(0:m + 1,0:n + 1).
Another device which will simplify the problem is to predefine the possible directions to move in a table, MOVE(1:8.1:2), which has the values
By equating the compass names with the numbers 1,2, ...,8 we make it easy to move in any direction. If we are at position (i,j) in the maze and we want to find the position (g,h) which is southwest of i,j, then we set
g
For example, if we are at position (3,4), then position (3 + 1 = 4, 4 +(-1) = 3) is southwest.
As we move through the maze we may have the chance to go in several directions. Not knowing which one to choose, we pick one but save our current position and the direction of the last move in a list. This way if we have taken a false path we can return and try another direction. With each new location we will examine the possibilities, starting from the north and looking clockwise. Finally, in order to prevent us from going down the same path twice we use another array MARK(0:m + 1,0:n + 1) which is initially zero. MARK(i,j) is set to 1 once we arrive at that position. We assume MAZE(m,n) = 0 as otherwise there is no path to the exit. We are now ready to write a first pass at an algorithm.
This is not a SPARKS program and yet it describes the essential processing without too much detail. The use of indentation for delineating important blocks of code plus the use of SPARKS key words make the looping and conditional tests transparent.
What remains to be pinned down? Using the three arrays MAZE, MARK and MOVE we need only specify how to represent the list of new triples. Since the algorithm calls for removing first the most recently entered triple, this list should be a stack. We can use the sequential representation we saw before. All we need to know now is a reasonable bound on the size of this stack. Since each position in the maze is visited at most once, at most mn elements can be placed into the stack. Thus mn locations is a safe but somewhat conservative bound. In the following maze
the only path has at most
Now, what can we say about the computing time for this algorithm? It is interesting that even though the problem is easy to grasp, it is difficult to make any but the most trivial statement about the computing time. The reason for this is because the number of iterations of the main while loop is entirely dependent upon the given maze. What we can say is that each new position (i,j) that is visited gets marked, so paths are never taken twice. There are at most eight iterations of the inner while loop for each marked position. Each iteration of the inner while loop takes a fixed amount of time, O(1), and if the number of zeros in MAZE is z then at most z positions can get marked. Since z is bounded above by mn, the computing time is bounded by
When pioneering computer scientists conceived the idea of higher level programming languages, they were faced with many technical hurdles. One of the biggest was the question of how to generate machine language instructions which would properly evaluate any arithmetic expression. A complex assignment statement such as
X
might have several meanings; and even if it were uniquely defined, say by a full use of parentheses, it still seemed a formidable task to generate a correct and reasonable instruction sequence. Fortunately the solution we have today is both elegant and simple. Moreover, it is so simple that this aspect of compiler writing is really one of the more minor issues.
An expression is made up of operands, operators and delimiters. The expression above has five operands: A,B,C,D, and E. Though these are all one letter variables, operands can be any legal variable name or constant in our programming language. In any expression the values that variables take must be consistent with the operations performed on them. These operations are described by the operators. In most programming languages there are several kinds of operators which correspond to the different kinds of data a variable can hold. First, there are the basic arithmetic operators: plus, minus, times, divide, and exponentiation (+,-,*,/,**). Other arithmetic operators include unary plus, unary minus and mod, ceil, and floor. The latter three may sometimes be library subroutines rather than predefined operators. A second class are the relational operators:
The first problem with understanding the meaning of an expression is to decide in what order the operations are carried out. This means that every language must uniquely define such an order. For instance, if A = 4, B = C = 2, D = E = 3, then in eq. 3.1 we might want X to be assigned the value
However, the true intention of the programmer might have been to assign X the value
Of course, he could specify the latter order of evaluation by using parentheses:
X
To fix the order of evaluation, we assign to each operator a priority. Then within any pair of parentheses we understand that operators with the highest priority will be evaluated first. A set of sample priorities from PL/I is given in Figure 3.7.
Notice that all of the relational operators have the same priority. Similarly, exponentiation, unary minus, unary plus and Boolean negation all have top priority. When we have an expression where two adjacent operators have the same priority, we need a rule to tell us which one to perform first. For example, do we want the value of - A ** B to be understood as (-A) ** B or -(A ** B)? Convince yourself that there will be a difference by trying A = -1 and B = 2. From algebra we normally consider A ** B ** C as A ** (B ** C) and so we rule that operators in priority 6 are evaluated right-to-left. However, for expressions such as A * B/ C we generally execute left-to-right or (A * B)/C. So we rule that for all other priorities, evaluation of operators of the same priority will proceed left to right. Remember that by using parentheses we can override these rules, and such expressions are always evaluated with the innermost parenthesized expression first.
Now that we have specified priorities and rules for breaking ties we know how X
X
How can a compiler accept such an expression and produce correct code? The answer is given by reworking the expression into a form we call postfix notation. If e is an expression with operators and operands, the conventional way of writing e is called infix, because the operators come in-between the operands. (Unary operators precede their operand.) The postfix form of an expression calls for each operator to appear after its operands. For example,
infix: A * B/C has postfix: AB * C/.
If we study the postfix form of A * B/C we see that the multiplication comes immediately after its two operands A and B. Now imagine that A * B is computed and stored in T. Then we have the division operator, /, coming immediately after its two arguments T and C.
Let us look at our previous example
infix: A/B ** C + D * E - A * C
postfix: ABC ** /DE * + AC * -
and trace out the meaning of the postfix.
Every time we compute a value let us store it in the temporary location Ti, i
So T6 will contain the result. Notice that if we had parenthesized the expression, this would change the postfix only if the order of normal evaluation were altered. Thus, A / (B ** C) + (D * E) - A * C will have the same postfix form as the previous expression without parentheses. But (A / B) ** (C + D) * (E - A ) * C will have the postfix form AB / CD + ** EA - * C *.
Before attempting an algorithm to translate expressions from infix to postfix notation, let us make some observations regarding the virtues of postfix notation that enable easy evaluation of expressions. To begin with, the need for parentheses is elimlnated. Secondly, the priority of the operators is no longer relevant. The expression may be evaluated by making a left to right scan, stacking operands, and evaluating operators using as operands the correct number from the stack and finally placing the result onto the stack. This evaluation process is much simpler than attempting a direct evaluation from infix notation.
To see how to devise an algorithm for translating from infix to postfix, note that the order of the operands in both forms is the same. In fact, it is simple to describe an algorithm for producing postfix from infix:
1) fully parenthesize the expression;
2) move all operators so that they replace their corresponding right parentheses;
3) delete all parentheses.
For example, A/B ** C + D * E - A * C when fully parenthesized yields
The arrows point from an operator to its corresponding right parenthesis. Performing steps 2 and 3 gives
ABC ** / DE * + AC * -.
The problem with this as an algorithm is that it requires two passes: the first one reads the expression and parenthesizes it while the second actually moves the operators. As we have already observed, the order of the operands is the same in infix and postfix. So as we scan an expression for the first time, we can form the postfix by immediately passing any operands to the output. Then it is just a matter of handling the operators. The solution is to store them in a stack until just the right moment and then to unstack and pass them to the output.
For example, since we want A + B * C to yield ABC * + our algorithm should perform the following sequence of stacking (these stacks will grow to the right):
At this point the algorithm must determine if * gets placed on top of the stack or if the + gets taken off. Since * has greater priority we should stack * producing
Now the input expression is exhausted, so we output all remaining operators in the stack to get
ABC * +
For another example, A * (B + C) * D has the postfix form ABC + * D *, and so the algorithm should behave as
At this point we want to unstack down to the corresponding left parenthesis, and then delete the left and right parentheses; this gives us:
These examples should motivate the following hierarchy scheme for binary arithmetic operators and delimiters. The general case involving all the operators of figure 3.7 is left as an exercise.
The rule will be that operators are taken out of the stack as long as their in-stack priority, isp, is greater than or equal to the in-coming priority, icp of the new operator. ISP(X) and ICP(X) are functions which reflect the table of figure 3.8.
As for the computing time, the algorithm makes only one pass across the input. If the expression has n symbols, then the number of operations is proportional to some constant times n. The stack cannot get any deeper than the number of operators plus 1, but it may achieve that bound as it does for A + B * C ** D.
Up to now we have been concerned only with the representation of a single stack or a single queue in the memory of a computer. For these two cases we have seen efficient sequential data representations. What happens when a data representation is needed for several stacks and queues? Let us once again limit ourselves, to sequential mappings of these data objects into an array V(1:m). If we have only 2 stacks to represent. then the solution is simple. We can use V(1) for the bottom most element in stack 1 and V(m) for the corresponding element in stack 2. Stack 1 can grow towards V(m) and stack 2 towards V(1). It is therefore possible to utilize efficiently all the available space. Can we do the same when more than 2 stacks are to be represented? The answer is no, because a one dimensional array has only two fixed points V(1) and V(m) and each stack requires a fixed point for its bottommost element. When more than two stacks, say n, are to be represented sequentially, we can initially divide out the available memory V(1:m) into n segments and allocate one of these segments to each of the n stacks. This initial division of V(1:m) into segments may be done in proportion to expected sizes of the various stacks if the sizes are known. In the absence of such information, V(1:m) may be divided into equal segments. For each stack i we shall use B(i) to represent a position one less than the position in V for the bottommost element of that stack. T(i), 1
B (i) = T (i) =
as the initial values of B(i) and T(i), (see figure 3.9). Stack i, 1
The algorithms to add and delete appear to be a simple as in the case of only 1 or 2 stacks. This really is not the case since the STACK_FULL condition in algorithm ADD does not imply that all m locations of V are in use. In fact, there may be a lot of unused space between stacks j and j + 1 for 1
Several strategies are possible for the design of algorithm STACK_FULL. We shall discuss one strategy in the text and look at some others in the exercises. The primary objective of algorithm STACK_FULL is to permit the adding of elements to stacks so long as there is some free space in V. One way to guarantee this is to design STACK_FULL along the following lines:
a) determine the least j, i < j
b) if there is no j as in a), then look to the left of stack i. Find the largest j such that 1
c) if there is no j satisfying either the conditions of a) or b), then all m spaces of V are utilized and there is no free space.
The writing of algorithm STACK_FULL using the above strategy is left as an exercise. It should be clear that the worst case performance of this representation for the n stacks together with the above strategy for STACK_FULL would be rather poor. In fact, in the worst case O(m) time may be needed for each insertion (see exercises). In the next chapter we shall see that if we do not limit ourselves to sequential mappings of data objects into arrays, then we can obtain a data representation for m stacks that has a much better worst case performance than the representation described here. Sequential representations for n queues and other generalizations are discussed in the exercises.
1. Consider a railroad switching network as below
Railroad cars numbered 1,2,3 ...,n are at the right. Each car is brought into the stack and removed at any time. For instance, if n = 3, we could move 1 in, move 2 in, move 3 in and then take the cars out producing the new order 3,2,1. For n = 3 and 4 what are the possible permutations of the cars that can be obtained? Are any permutations not possible?
2. Using a Boolean variable to distinguish between a circular queue being empty or full, write insert and delete procedures.
3. Complete the correctness proof for the stack implementation of section 3.1.
4. Use the queue axioms to prove that the circular queue representation of section 3.1 is correct.
5. A double ended queue (deque) is a linear list in which additions and deletions may be made at either end. Obtain a data representation mapping a deque into a one dimensional array. Write algorithms to add and delete elements from either end of the deque.
6. [Mystery function] Let f be an operation whose argument and result is a queue and which is defined by the axioms:
what does f do?
7. A linear list is being maintained circularly in an array C(0: n - 1) with F and R set up as for circular queues.
a) Obtain a formula in terms of F, R and n for the number of elements in the list.
b) Write an algorithm to delete the k'th element in the list.
c) Write an algorithm to insert an element Y immediately after the k'th element .
What is the time complexity of your algorithms for b) and c)?
8. Let L = (a1,a2, ...,an) be a linear list represented in the array V(1:n) using the mapping: the i'th element of L is stored in V(i). Write an algorithm to make an inplace reversal of the order of elements in V. I.e., the algorithm should transform V such that V(i) contains the n - i + 1'st element of L. The only additional space available to your algorithm is that for simple variables. The input to the algorithm is V and n. How much time does your algorithm take to accomplish the reversal?
9. a) Find a path through the maze of figure 3.5.
b) Trace out the action of procedure PATH on the maze of figure 3.5. Compare this to your own attempt in a).
10. What is the maximum path length from start to finish in any maze of dimensions n X m?
11. Write the postfix form of the following expressions:
a) A ** B ** C
b) -A + B - C + D
c) A ** -B + C
d) (A + B) * D + E/(F + A * D) + C
12. Obtain isp and icp priorities for all the operators of figure 3.7 together with the delimiters '(',and')'. These priorities should be such that algorithm POSTFIX correctly generates the postfix form for all expressions made up of operands and these operators and delimiters.
13. Use the isp and icp priorities obtained in exercise 12 to answer the following:
a) In algorithm POSTFIX what is the maximum number of elements that can be on the stack at any time if the input expression E has n operators and delimiters?
b) What is the answer to a) if E contains no operators of priority 6, has n operators and the depth of nesting of parentheses is at most 6?
14. Another expression form that is easy to evaluate and is parenthesis free is known as prefix. In this way of writing expressions, the operators precede their operands. For example:
Notice that the order of operands is not changed in going from infix to prefix .
a) What is the prefix form of the expressions in exercise 11.
b) Write an algorithm to evaluate a prefix expression, E (Hint: Scan E right to left and assume that the leftmost token of E is '
c) Write an algorithm to transform an infix expression E into its prefix equivalent. Assume that the input expression E begins with a '
What is the time complexity of your algorithms for b) and c)? How much space is needed by each of these algorithms?
15. Write an algorithm to transform from prefix to postfix. Carefully state any assumptions you make regarding the input. How much time and space does your algorithm take?
16. Do exercise 15 but this time for a transformation from postfix to prefix.
17. Write an algorithm to generate fully parenthesized infix expressions from their postfix form. What is the complexity (time and space) of your algorithm?
18. Do exercise 17 starting from prefix form.
19. Two stacks are to be represented in an array V(1:m) as described in section 3.4. Write algorithms ADD(i.X) and DELETE(i) to add X and delete an element from stack i, 1
20. Obtain a data representation mapping a stack S and a queue Q into a single array V(1:n). Write algorithms to add and delete elements from these two data objects. What can you say about the suitability of your data representation?
21. Write a SPARKS algorithm implementing the strategy for STACK_FULL(i) outlined in section 3.4.
22. For the ADD and DELETE algorithms of section 3.4 and the STACK_FULL(i) algorithm of exercise 21 produce a sequence of adds and deletes that will require O(m) time for each add. Use n = 2 and start from a configuration representing a full utilization of V(1:m).
23. It has been empirically observed that most programs that get close to using all available space eventually run out of space. In the light of this observation, it seems futile to move stacks around providing space for other stacks to grow in if there is only a limited amount of space that is free. Rewrite the algorithm of exercise 21 so that the algorithm terminates if there are fewer than C free spaces. C is an empirically determined constant and is provided to the algorithm.
24. Another strategy for the STACK_FULL(i) condition of section 3.4 is to redistribute all the free space in proportion to the rate of growth of individual stacks since the last call to STACK_FULL. This would require the use of another array LT(1:n) where LT(j) is the value of T(j) at the last call to STACK_FULL. Then the amount by which each stack has grown since the last call is T(j) - LT(j). The figure for stack i is actually T(i) - LT(i) + 1, since we are now attempting to add another element to i.
Write algorithm STACK_FULL (i) to redistribute all the stacks so that the free space between stacks j and j + 1 is in proportion to the growth of stack j since the last call to STACK_FULL. STACK_FULL (i) should assign at least 1 free location to stack i.
25. Design a data representation sequentially mapping n queues into all array V(1:m). Represent each queue as a circular queue within V. Write algorithms ADDQ, DELETEQ and QUEUE-FULL for this representation.
26. Design a data representation, sequentially mapping n data objects into an array V(1:m). n1 of these data objects are stacks and the remaining n2 = n - n1 are queues. Write algorithms to add and delete elements from these objects. Use the same SPACE_FULL algorithm for both types of data objects. This algorithm should provide space for the i-th data object if there is some space not currently being used. Note that a circular queue with space for r elements can hold only r - 1.
27. [Landweber]
People have spent so much time playing card games of solitaire that the gambling casinos are now capitalizing on this human weakness. A form of solitaire is described below. Your assignment is to write a computer program to play the game thus freeing hours of time for people to return to more useful endeavors.
To begin the game, 28 cards are dealt into 7 piles. The leftmost pile has 1 card, the next two cards, and so forth up to 7 cards in the rightmost pile. Only the uppermost card of each of the 7 piles is turned face up. The cards are dealt left to right, one card to each pile, dealing to one less pile each time, and turning the first card in each round face up.
On the top-most face up card of each pile you may build in descending sequences red on black or black on red. For example, on the 9 of spades you may place either the 8 of diamonds or the 8 of hearts. All face up cards on a pile are moved as a unit and may be placed on another pile according to the bottommost face up card. For example, the 7 of clubs on the 8 of hearts may be moved as a unit onto the 9 of clubs or the 9 of spades.
Whenever a face down card is uncovered, it is turned face up. If one pile is removed completely, a face-up King may be moved from a pile (together with all cards above it) or the top of the waste pile (see below)) into the vacated space. There are four output piles, one for each suit, and the object of the game is to get as many cards as possible into the output piles. Each time an Ace appears at the top of a pile or the top of the stack it is moved into the appropriate output pile. Cards are added to the output piles in sequence, the suit for each pile being determined by the Ace on the bottom.
From the rest of the deck, called the stock, cards are turned up one by one and placed face up on a waste pile. You may always play cards off the top of the waste pile, but only one at a time. Begin by moving a card from the stock to the top of the waste pile. If there is ever more than one possible play to be made, the following order must be observed:
i) Move a card from the top of a playing pile or from the top of the waste pile to an output pile. If the waste pile becomes empty, move a card from the stock to the waste pile.
ii) Move a card from the top of the waste pile to the leftmost playing pile to which it can be moved. If the waste pile becomes empty move a card from the stock to the waste pile.
iii) Find the leftmost playing pile which can be moved and place it on top of the leftmost playing pile to which it can be moved.
iv) Try i), ii) and iii) in sequence, restarting with i) whenever a move is made.
v) If no move is made via (i)-(iv) move a card from the stock to the waste pile and retry (i).
Only the topmost card of the playing piles or the waste pile may be played to an output pile. Once played on an output pile, a card may not be withdrawn to help elsewhere. The game is over when either
i) all the cards have been played to the output or
ii) the stock pile has been exhausted and no more cards can be moved
When played for money, the player pays the house $52 at the beginning and wins $5 for every card played to the output piles.
Write your program so that it will play several games, and determine your net winnings. Use a random number generator to shuffle the deck.
Output a complete record of two games in easily understood form. Include as output the number of games played and the net winning (+ or -).
structure STACK (item)
1 declare CREATE ( )
 stack
stack2 ADD (item, stack)
 stack
stack3 DELETE (stack)
 stack
stack4 TOP (stack)
 item
item5 ISEMTS (stack)
 boolean;
boolean;6 for all S
 stack, i
stack, i  item let
item let7 ISEMTS (CREATE) :: = true
8 ISEMTS (ADD (i,S)) :: = false
9 DELETE (CREATE) :: = error
10 DELETE (ADD (i,S)) :: = S
11 TOP(CREATE) :: = error
12 TOP(ADD(i,S)) :: = i
13 end
end STACK
CREATE ( ) :: = declare STACK(1:n); top
 0
0ISEMTS(STACK) :: = if top = 0 then true
else false
TOP(STACK) :: = if top = 0 then error
else STACK(top)
procedure ADD (item, STACK, n, top)
//insert item into the STACK of maximum size n; top is the number
of elements curently in STACK//
if top
 n then call STACK_FULL
n then call STACK_FULLtop
 top + 1
top + 1STACK (top)
 item
itemend ADD
procedure DELETE (item, STACK, top)
//removes the top element of STACK and stores it in item
unless STACK is empty//
if top
 0 then call STACK_EMPTY
0 then call STACK_EMPTYitem
 STACK (top)
STACK (top)top
 top - 1
top - 1end DELETE
structure QUEUE (item)
1 declare CREATEQ( )
 queue
queue2 ADDQ(item,queue)
 queue
queue3 DELETEQ(queue)
 queue
queue4 FRONT(queue)
 item
item5 ISEMTQ(queue)
 boolean;
boolean;6 for all Q
 queue, i
queue, i  item let
item let7 ISEMTQ(CREATEQ) :: = true
8 ISEMTQ(ADDQ(i,Q)) :: = false
9 DELETEQ(CREATEQ) :: = error
10 DELETEQ(ADDQ(i,Q)):: =
11 if ISEMTQ(Q) then CREATEQ
12 else ADDQ(i,DELETEQ(Q))
13 FRONT(CREATEQ) :: = error
14 FRONT(ADDQ(i,Q)) :: =
15 if ISEMTQ(Q) then i else FRONT(Q)
16 end
17 end QUEUE
Q(1) (2) (3) (4) (5) (6) (7) ... Remarks
front rear
0 0 queue empty Initial
0 1 Jl Job 1 joins Q
0 2 J1 J2 Job 2 joins Q
0 3 J1 J2 J3 Job 3 joins Q
1 3 J2 J3 Job 1 leaves Q
1 4 J2 J3 J4 Job 4 joins Q
2 4 J3 J4 Job 2 leaves Q
CREATEQ(Q) :: = declare Q(l:n); front
 rear
rear  0
0ISEMTQ(Q) :: = if front = rear then true
else false
FRONT(Q) :: = if ISEMTQ(Q) then error
else Q(front + 1)
procedure ADDQ(item, Q, n, rear)
//insert item into the queue represented in Q(l:n)//
if rear = n then call QUEUE_FULL
rear
 rear + 1
rear + 1 Q(rear)
 item
itemend ADDQ
procedure DELETEQ(item, Q, front, rear)
//delete an element from a queue//
if front = rear then call QUEUE_EMPTY
front
 front + 1
front + 1 item
 Q(front)
Q(front)end DELETEQ

Figure 3.3
if rear = n - 1 then rear
 0
0else rear
 rear + 1.
rear + 1.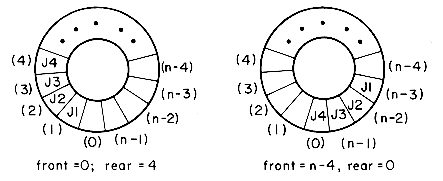
Figure 3.4: Circular queue of n elements and four jobs J1, J2, J3, J4
 (rear + 1)mod n. Similarly, it will be necessary to move front one position clockwise each time a deletion is made. Again, using the modulo operation, this can be accomplished by front
(rear + 1)mod n. Similarly, it will be necessary to move front one position clockwise each time a deletion is made. Again, using the modulo operation, this can be accomplished by front  (front + l)mod n. An examination of the algorithms indicates that addition and deletion can now be carried out in a fixed amount of time or O(1).
(front + l)mod n. An examination of the algorithms indicates that addition and deletion can now be carried out in a fixed amount of time or O(1).procedure ADDQ(item, Q, n, front, rear)
//insert item in the circular queue stored in Q(0:n - 1);
rear points to the last item and front is one position
counterclockwise from the first item in Q//
rear
 (rear + l)mod n //advance rear clockwise//
(rear + l)mod n //advance rear clockwise//if front = rear then call QUEUE-FULL
Q(rear)
 item //insert new item//
item //insert new item//end ADDQ
procedure DELETEQ(item, Q, n, front, rear)
//removes the front element of the queue Q(0:n - 1)//
if front = rear then call QUEUE-EMPTY
front
 (front + 1)mod n //advance front clockwise//
(front + 1)mod n //advance front clockwise//item
 Q(front) //set item to front of queue//
Q(front) //set item to front of queue//end DELETEQ
3.2 A MAZING PROBLEM

Figure 3.5
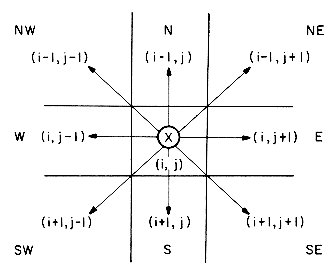
Figure 3.6
MOVE 1 2
-- --
(1) -1 0 north
(2) -1 1 northeast
(3) 0 1 east
(4) 1 1 southeast
(5) 1 0 south
(6) 1 -1 southwest
(7) 0 -1 west
(8) -1 -1 northwest
 i + MOVE(6,1); h
i + MOVE(6,1); h j + MOVE(6,2)
j + MOVE(6,2)set list to the maze entrance coordinates and direction north;
while list is not empty do
(i,j, mov)
 coordinates and direction from front of list
coordinates and direction from front of listwhile there are more moves do
(g,h)
 coordinates of next move
coordinates of next moveif (g,h) = (m,n) then success
if MAZE (g,h) = 0 //the move is legal//
and MARK (g,h) = 0 //we haven't been here before//
then [MARK (g,h)
 1
1add (i,j, mov) to front of list
(i,j,mov)
 (g,h, null)]
(g,h, null)]end
end
print no path has been found

 m/2
m/2 (n + 1) positions. Thus mn is not too crude a bound. We are now ready to give a precise maze algorithm.
(n + 1) positions. Thus mn is not too crude a bound. We are now ready to give a precise maze algorithm.procedure PATH (MAZE, MARK, m, n, MOVE, STACK)
//A binary matrix MAZE (0:m + 1, 0:n + 1) holds the maze.
MARK (0:m + 1, 0:n + 1) is zero in spot (i,j) if MAZE (i,j) has not
yet been reached. MOVE (8,2) is a table used to change coordinates
(i,j) to one of 8 possible directions. STACK (mn,3) holds the
current path// MARK (1,1)
 1
1(STACK(1,1),STACK(1,2),STACK(1,3))
 (1,1,2);top
(1,1,2);top  1
1while top
 0 do
0 do(i,j,mov)
 (STACK(top,1),STACK(top,2), STACK(top,3) + 1)
(STACK(top,1),STACK(top,2), STACK(top,3) + 1)top
 top - 1
top - 1while mov
 8 do
8 dog
 i + MOVE (mov,1); h
i + MOVE (mov,1); h  j + MOVE(mov,2)
j + MOVE(mov,2)if g = m and h = n
then [for p
 1 to top do //goal//
1 to top do //goal//print (STACK(p,1),STACK(p,2)
end
print(i,j); print(m,n);return]
if MAZE(g,h) = 0 and MARK(g,h) = 0
then[MARK(g,h)
 1
1top
 top + 1
top + 1(STACK(top,1),STACK(top,2),STACK(top,3))

(i,j,mov) //save (i,j) as part of current path//
mov
 0; i
0; i  g; j
g; j  h]
h]mov
 mov + 1 //point to next direction//
mov + 1 //point to next direction//end
end
print ('no path has been found')end PATH
 . (In actual experiments, however, the rat may be inspired by the watching psychologist and the invigorating odor from the cheese at the exit. It might reach its goal by examining far fewer paths than those examined by algorithm PATH. This may happen despite the fact that the rat has no pencil and only a very limited mental stack. It is difficult to incorporate the effect of the cheese odor and the cheering of the psychologists into a computer algorithm.) The array MARK can be eliminated altogether and MAZE(i,j) changed to 1 instead of setting MARK(i,j) to 1, but this will destroy the original maze.
. (In actual experiments, however, the rat may be inspired by the watching psychologist and the invigorating odor from the cheese at the exit. It might reach its goal by examining far fewer paths than those examined by algorithm PATH. This may happen despite the fact that the rat has no pencil and only a very limited mental stack. It is difficult to incorporate the effect of the cheese odor and the cheering of the psychologists into a computer algorithm.) The array MARK can be eliminated altogether and MAZE(i,j) changed to 1 instead of setting MARK(i,j) to 1, but this will destroy the original maze.3.3 EVALUATION OF EXPRESSIONS
 A/B ** C + D* E - A * C
A/B ** C + D* E - A * C(3.1)
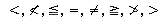 . These are usually defined to work for arithmetic operands, but they can just as easily work for character string data. ('CAT' is less than 'DOG' since it precedes 'DOG' in alphabetical order.) The result of an expression which contains relational operators is one of the two constants: true or false. Such all expression is called Boolean, named after the mathematician George Boole, the father of symbolic logic.
. These are usually defined to work for arithmetic operands, but they can just as easily work for character string data. ('CAT' is less than 'DOG' since it precedes 'DOG' in alphabetical order.) The result of an expression which contains relational operators is one of the two constants: true or false. Such all expression is called Boolean, named after the mathematician George Boole, the father of symbolic logic.4/(2 ** 2) + (3 * 3) - (4 * 2)
= (4/4) + 9 - 8
= 2.
(4/2) ** (2 + 3) * (3 - 4) * 2
= (4/2) ** 5* -1 * 2
= (2**5)* -2
= 32* -2
= -64.
 ((((A/ B) ** (C + D)) * (E - A)) * C).
((((A/ B) ** (C + D)) * (E - A)) * C).
Figure 3.7. Priority of arithmetic, Boolean and relational operators
 A/B ** C + D * E - A * C will be evaluated, namely as
A/B ** C + D * E - A * C will be evaluated, namely as ((A/(B** C)) + (D* E)) - (A * C).
((A/(B** C)) + (D* E)) - (A * C).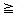 1. Reading left to right, the first operation is exponentiation:
1. Reading left to right, the first operation is exponentiation:Operation Postfix
--------- -------
T1
 B **C AT1/DE * + AC * -
B **C AT1/DE * + AC * -T2
 A/T1 T2DE * + AC * -
A/T1 T2DE * + AC * -T3
 D * E T2T3 + AC * -
D * E T2T3 + AC * -T4
 T2 + T3 T4AC * -
T2 + T3 T4AC * -T5
 A * C T4T5 -
A * C T4T5 -T6
 T4, - T5 T6
T4, - T5 T6procedure EVAL (E)
//evaluate the postfix expression E. It is assumed that the
last character in E is an '
 '. A procedure NEXT-TOKEN is
'. A procedure NEXT-TOKEN isused to extract from E the next token. A token is either a
operand, operator, or '
 '. A one dimensional array STACK(l:n) is
'. A one dimensional array STACK(l:n) isused as a stack//
top
 0 // initialize STACK//
0 // initialize STACK//loop
x
 NEXT-TOKEN (E)
NEXT-TOKEN (E)case
: x = '
 ' : return//answer is at top of stack//
' : return//answer is at top of stack//: x is an operand: call ADD(x,STACK,n,top)
:else: remove the correct number of operands
for operator x from STACK, perform
the operation and store the result, if
any, onto the stack
end
forever
end EVAL

Next Token Stack Output
---------- ----- ------
none empty none
A empty A
+ + A
B + AB
* + * AB
C + * ABC
Next Token Stack Output
---------- ----- ------
none empty none
A empty A
* * A
( *( A
B *( AB
+ *(+ AB
C *(+ ABC
) * ABC +
* * ABC + *
D * ABC + * D
done empty ABC + * D *
Symbol In-Stack Priority In-Coming Priority
------ ----------------- ------------------
) - -
** 3 4
*,/ 2 2
binary +,- 1 1
( 0 4
Figure 3.8 Priorities of Operators for Producing Postfix
procedure POSTFIX (E)
//convert the infix expression E to postfix. Assume the last
character of E is a '
 ', which will also be the last character of
', which will also be the last character ofthe postfix. Procedure NEXT-TOKEN returns either the next
operator, operand or delimiter--whichever comes next.
STACK (1:n) is used as a stack and the character '-
 ' with
' withISP('- ') = -1 is used at the bottom of the stack. ISP and ICP
') = -1 is used at the bottom of the stack. ISP and ICPare functions.//
STACK(1)
 '-
'- '; top
'; top  1 //initialize stack//
1 //initialize stack//loop
x
 NEXT-TOKEN(E)
NEXT-TOKEN(E)case
:x = '
 ': while top > 1 do //empty the stack//
': while top > 1 do //empty the stack//print(STACK(top));top
 top - 1
top - 1end
print (' ')
')return
:x is an operand: print (x)
:x = ')': while STACK(top)
 '(' do// unstack until '('//
'(' do// unstack until '('//print (STACK(top));top
 top - 1
top - 1end
top
 top - 1 //delete')'//
top - 1 //delete')'//:else while ISP(STACK(top))
 ICP(x) do
ICP(x) doprint (STACK(top)); top
 top - 1
top - 1end
call ADD(x,STACK,n,top) //insert x in STACK//
end
forever
end POSTFIX
3.4 MULTIPLE STACKS AND QUEUES
 i
i  n will point to the topmost element of stack i. We shall use the boundary condition B(i) = T(i) iff the i'th stack is empty. If we grow the i'th stack in lower memory indexes than the i + 1'st, then with roughly equal initial segments we have
n will point to the topmost element of stack i. We shall use the boundary condition B(i) = T(i) iff the i'th stack is empty. If we grow the i'th stack in lower memory indexes than the i + 1'st, then with roughly equal initial segments we have m/n
m/n (i - 1), 1
(i - 1), 1  i
i  n
n(3.2)
 i
i  n can grow from B(i) + 1 up to B(i + 1) before it catches up with the i + 1'st stack. It is convenient both for the discussion and the algorithms to define B(n + 1) = m. Using this scheme the add and delete algorithms become:
n can grow from B(i) + 1 up to B(i + 1) before it catches up with the i + 1'st stack. It is convenient both for the discussion and the algorithms to define B(n + 1) = m. Using this scheme the add and delete algorithms become:procedure ADD(i,X)
//add element X to the i'th stack, 1
 i
i  n//
n//if T(i) = B(i + 1) then call STACK-FULL (i)
T(i)
 T(i) + 1
T(i) + 1V(T(i))
 X //add X to the i'th stack//
X //add X to the i'th stack//end ADD
procedure DELETE(i,X)
//delete topmost element of stack i//
if T(i) = B(i) then call STACK-EMPTY(i)
X
 V(T(i))
V(T(i))T(i)
 T(i) - 1
T(i) - 1end DELETE
 j
j  n and j
n and j  i (figure 3.10). The procedure STACK_FULL (i) should therefore determine whether there is any free space in V and shift stacks around so as to make some of this free space available to the i'th stack.
i (figure 3.10). The procedure STACK_FULL (i) should therefore determine whether there is any free space in V and shift stacks around so as to make some of this free space available to the i'th stack. n such that there is free space between stacks j and j + 1, i.e., T(j) < B(j + 1). If there is such a j, then move stacks i + 1, i + 2, ...,j one position to the right (treating V(1) as leftmost and V(m) as rightmost), thereby creating a space between stacks i and i + 1.
n such that there is free space between stacks j and j + 1, i.e., T(j) < B(j + 1). If there is such a j, then move stacks i + 1, i + 2, ...,j one position to the right (treating V(1) as leftmost and V(m) as rightmost), thereby creating a space between stacks i and i + 1. j < i and there is space between stacks j and j + 1, i.e., T(j) < B(j + 1). If there is such a j, then move stacks j + 1, j + 2, ...,i one space left creating a free space between stacks i and i + 1.
j < i and there is space between stacks j and j + 1, i.e., T(j) < B(j + 1). If there is such a j, then move stacks j + 1, j + 2, ...,i one space left creating a free space between stacks i and i + 1.
Figure 3.9 Initial configuration for n stacks in V(1:m). All stacks are empty and memory is divided into roughly equal segments.
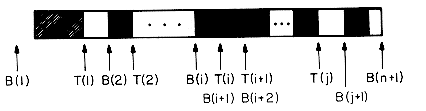
Figure 3.10 Configuration when stack i meets with stack i + 1 but there is still free space elsewhere in V.
EXERCISES
f(CREATEQ) :: = CREATEQ
f(ADDQ(i,q)) :: = if ISEMTQ(q) then ADDQ(i,q)
else ADDQ(FRONT(q), f(DELETEQ(ADDQ(i,q))))
infix prefix
-----------------------------------------------
A * B/C /* ABC
A/B ** C + D * E - A * C - +/A ** BC * DE * AC
A * (B + C)/D - G -/* A + BCDG
 '.)
'.) ' and that the prefix expression should begin with a '
' and that the prefix expression should begin with a ' '.
'. i
i  2. Your algorithms should be able to add elements to the stacks so long as there are fewer than m elements in both stacks together.
2. Your algorithms should be able to add elements to the stacks so long as there are fewer than m elements in both stacks together.


