Suppose n keys, k1, k2, . . . , kn, are stored at the internal nodes of a binary search tree. It is assumed that the keys are given in sorted order, so that k1 < k2 < . . . < kn. An extended binary search tree is obtained from the binary search tree by adding successor nodes to each of its terminal nodes as indicated in Figure 12.9 by ?/FONT>'s.
Although the programming goal in this chapter is to find optimal binary search trees, extended binary search trees are used along the way. In the extended tree, the ?/FONT>'s represent terminal nodes, while the other nodes are internal nodes. These terminal nodes represent unsuccessful searches of the tree for key values. Such searches do not end successfully because the search key is not actually stored in the tree. They actually terminate when a null subtree pointer is encountered along the search path.
In general, the terminal node in the extended tree that is the left successor of k1 can be interpreted as representing all key values that are not stored and are less than k1. Similarly, the terminal node in the extended tree that is the right successor of kn represents all key values not stored in the tree that are greater than kn. The terminal node that is accessed between ki and ki+1 in an inorder traversal represents all key values not stored that lie between ki and ki+1. For example, in the extended tree in Figure 12.9(b), if the possible key values are 0,1, 2, 3, . . . ,100, then the terminal node labeled 0 represents the missing key values 0,1, and 2 if k1 is 3. The terminal node labeled 3 represents the key values between k3 and k4. If k3 is 17 and k4 is 21, then the terminal node labeled 3 represents the missing key values 18,19, and 20. If k6 is 90, then terminal node 6 represents the missing key values 91 through 100.
Assuming that the relative frequency with which each key value is accessed is known, weights can be assigned to each node of the extended tree. The weights represent the relative frequencies of searches terminating at each node. The weighted path length of the extended tree is then a natural measure for the average time to search the binary search tree for a key.
Example 12.2
Find the extended binary search tree that has the minimal weighted path length. The optimal binary search tree is obtained from this tree simply by omitting the extended nodes. n
Before dealing with this problem, we compare it to the Huffman coding problem that has already been solved. When the weights attached to the internal nodes of the extended binary search tree are zero, this problem is similar to the Huffman coding problem. The difference is that the task now is to find the binary search tree with minimal weighted path length, whereas the Huffman algorithm finds the binary tree with minimal weighted path length. Since the binary search trees are only a subset of all binary trees, the Huffman tree will yield a value of the minimal weighted path length that is never larger than that of the optimal binary search tree. The Huffman algorithm will not solve the current problem unless, by chance, the tree that it constructs is a binary search tree or can be converted to one with no increase in the weighted path length. An algorithm, the Hu-Tucker algorithm, has been developed for this special case, and requires, as does the Huffman algorithm, time O(n lg n) and O(n) storage. Initially, its time was thought to be O(n2), but Knuth showed how to reduce this time by selecting the appropriate data structure. We now proceed to the general case in which the weights of the internal nodes need not be zero.
12.4.1 Finding Optimal Binary Search Trees

(a) Binary Search Tree
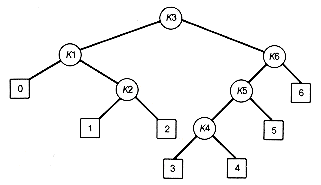
(b) Extended Binary Search Tree
Figure 12.9 Extension of a Binary Search Tree