 (n) time, but the straightforward method of multiplying them takes
(n) time, but the straightforward method of multiplying them takes  (n2) time. In this chapter, we shall show how the Fast Fourier Transform, or FFT, can reduce the time to multiply polynomials to
(n2) time. In this chapter, we shall show how the Fast Fourier Transform, or FFT, can reduce the time to multiply polynomials to  (nl n).
(nl n).


The straightforward method of adding two polynomials of degree n takes  (n) time, but the straightforward method of multiplying them takes
(n) time, but the straightforward method of multiplying them takes  (n2) time. In this chapter, we shall show how the Fast Fourier Transform, or FFT, can reduce the time to multiply polynomials to
(n2) time. In this chapter, we shall show how the Fast Fourier Transform, or FFT, can reduce the time to multiply polynomials to  (nl n).
(nl n).
Polynomials
A polynomial in the variable x over an algebraic field F is a function A(x) that can be represented as follows:
We call n the degree-bound of the polynomial, and we call the values a0, a1, . . ., an - 1 the coefficients of the polynomial. The coefficients are drawn from the field F, typically the set C of complex numbers. A polynomial A(x) is said to have degree k if its highest nonzero coefficient is ak. The degree of a polynomial of degree-bound n can be any integer between 0 and n - 1, inclusive. Conversely, a polynomial of degree k is a polynomial of degree-bound n for any n > k.
There are a variety of operations we might wish to define for polynomials. For polynomial addition, if A (x) and B (x) are polynomials of degree-bound n, we say that their sum is a polynomial C (x), also of degree-bound n, such that C (x) = A (x) + B (x) for all x in the underlying field. That is, if
and
then
where cj = aj + bj for j = 0,1, . . .,n - 1. For example, if A(x) = 6x3 + 7x2 - 10x + 9 and B(x) = -2x3+ 4x - 5, then C(x) = 4x3 + 7x2 - 6x + 4.
For polynomial multiplication, if A(x) and B(x) are polynomials of degree-bound n, we say that their product C(x) is a polynomial of degree-bound 2n - 1 such that C(x) = A(x)B(x) for all x in the underlying field. You have probably multiplied polynomials before, by multiplying each term in A(x) by each term in B(x) and combining terms with equal powers. For example, we can multiply A(x) = 6x3 + 7x2 - 10x + 9 and B(x) = -2x3 + 4x - 5 as follows:
Another way to express the product C(x) is
where
We shall nevertheless speak of the degree-bound of C as being the sum of the degree-bounds of A and B, since if a polynomial has degree-bound k it also has degree-bound k + 1.
Chapter outline
Section 32.1 presents two ways to represent polynomials: the coefficient representation and the point-value representation. The straightforward methods for multiplying polynomials--equations (32.1) and (32.2)--take
This chapter uses complex numbers extensively, and the symbol i will be used exclusively to denote
The coefficient and point-value representations of polynomials are in a sense equivalent; that is, a polynomial in point-value form has a unique counterpart in coefficient form. In this section, we introduce the two representations and show how they can be combined to allow multiplication of two degree-bound n polynomials in
A coefficient representation of a polynomial
The coefficient representation is convenient for certain operations on polynomials. For example, the operation of evaluating the polynomial A(x) at a given point x0 consists of computing the value of A(x0). Evaluation takes time
Similarly, adding two polynomials represented by the coefficient vectors a = (a0, a1, . . ., an-1) and b = (b0, b1, . . ., bn-1) takes
Now, consider the multiplication of two degree-bound n polynomials A(x) and B(x) represented in coefficient form. If we use the method described by equations (32.1) and (32.2), polynomial multiplication takes time
A point-value representation of a polynomial A(x) of degree-bound n is a set of n point-value pairs
such that all of the xk are distinct and
for k = 0, 1, . . ., n - 1. A polynomial has many different point-value representations, since any set of n distinct points x0, x1, . . ., xn-1 can be used as a basis for the representation.
Computing a point-value representation for a polynomial given in coefficient form is in principle straightforward, since all we have to do is select n distinct points x0, x1, . . ., xn-1 and then evaluate A(xk) for k = 0, 1, . . ., n - 1. With Horner's method, this n-point evaluation takes time
The inverse of evaluation--determining the coefficient form of a polynomial from a point-value representation--is called interpolation. The following theorem shows that interpolation is well defined, assuming that the degree-bound of the interpolating polynomial equals the number of given point-value pairs.
Theorem 32.1
For any set {(x0, y0), (x1, y1), . . ., (xn-1, yn-1)} of n point-value pairs, there is a unique polynomial A(x) of degree-bound n such that yk = A(xk) for k = 0, 1, . . ., n - 1.
Proof The proof is based on the existence of the inverse of a certain matrix. Equation (32.3) is equivalent to the matrix equation
The matrix on the left is denoted V(x0, x1, . . ., xn-1) and is known as a Vandermonde matrix. By Exercise 31.1-10, this matrix has determinant
and therefore, by Theorem 31.5, it is invertible (that is, nonsingular) if the xk are distinct. Thus, the coefficients aj can be solved for uniquely given the point-value representation:
The proof of Theorem 32.1 describes an algorithm for interpolation based on solving the set (32.4) of linear equations. Using the LU decomposition algorithms of Chapter 31, we can solve these equations in time O(n3).
A faster algorithm for n-point interpolation is based on Lagrange's formula:
You may wish to verify that the right-hand side of equation (32.5) is a polynomial of degree-bound n that satisfies A(xk) = yk for all k. Exercise 32.1-4 asks you how to compute the coefficients of A using Lagrange's formula in time
Thus, n-point evaluation and interpolation are well-defined inverse operations that transform between the coefficient representation of a polynomial and a point-value representation.1 The algorithms described above for these problems take time
1Interpolation is a notoriously tricky problem from the point of view of numerical stability. Although the approaches described here are mathematically correct, small differences in the inputs or round-off errors during computation can cause large differences in the result.
The point-value representation is quite convenient for many operations on polynomials. For addition, if C(x) = A(x) + B(x), then C(xk) = A(xk) + B(xk) for any point xk. More precisely, if we have a point-value representation for A,
and for B,
(note that A and B are evaluated at the same n points), then a point-value representation for C is
The time to add two polynomials of degree-bound n in point-value form is thus
Similarly, the point-value representation is convenient for multiplying polynomials. If C(x) = A(x)B(x), then C(xk) = A(xk)B(xk) for any point xk, and we can pointwise multiply a point-value representation for A by a point-value representation for B to obtain a point-value representation for C. We must face the problem, however, that the degree-bound of C is the sum of the degree-bounds for A and B. A standard point-value representation for A and B consists of n point-value pairs for each polynomial. Multiplying these together gives us n point-value pairs for C, but since the degree-bound of C is 2n, Theorem 32.1 implies that we need 2n point-value pairs for a point-value representation of C. We must therefore begin with "extended" point-value representations for A and for B consisting of 2n point-value pairs each. Given an extended point-value representation for A,
and a corresponding extended point-value representation for B,
then a point-value representation for C is
Given two input polynomials in extended point-value form, we see that the time to multiply them to obtain the point-value form of the result is
Finally, we consider how to evaluate a polynomial given in point-value form at a new point. For this problem, there is apparently no approach that is simpler than converting the polynomial to coefficient form first, and then evaluating it at the new point.
Can we use the linear-time multiplication method for polynomials in point-value form to expedite polynomial multiplication in coefficient form? The answer hinges on our ability to convert a polynomial quickly from coefficient form to point-value form (evaluate) and vice-versa (interpolate).
We can use any points we want as evaluation points, but by choosing the evaluation points carefully, we can convert between representations in only
Figure 32.1 shows this strategy graphically. One minor detail concerns degree-bounds. The product of two polynomials of degree-bound n is a polynomial of degree-bound 2n. Before evaluating the input polynomials A and B, therefore, we first double their degree-bounds to 2n by adding n high-order coefficients of 0. Because the vectors have 2n elements, we use "complex (2n)th roots of unity," which are denoted by the w2n terms in Figure 32.1.
Given the FFT, we have the following
1. Double degree-bound: Create coefficient representations of A(x) and B(x) as degree-bound 2n polynomials by adding n high-order zero coefficients to each.
2. Evaluate: Compute point-value representations of A(x) and B(x) of length 2n through two applications of the FFT of order 2n. These representations contain the values of the two polynomials at the (2n)th roots of unity.
3. Pointwise multiply: Compute a point-value representation for the polynomial C(x) = A(x)B(x) by multiplying these values together pointwise. This representation contains the value of C(x) at each (2n)th root of unity.
4. Interpolate: Create the coefficient representation of the polynomial C(x) through a single application of an FFT on 2n point-value pairs to compute the inverse DFT.
Steps (1) and (3) take time
Theorem 32.2
The product of two polynomials of degree-bound n can be computed in time
32.1-1
Multiply the polynomials A(x) = 7x3 - x2 + x - 10 and B(x) = 8x3 - 6x + 3 using equations (32.1) and (32.2).
32.1-2
Evaluating a polynomial A(x) of degree-bound n at a given point x0 can also be done by dividing A(x) by the polynomial (x - x0) to obtain a quotient polynomial q(x) of degree-bound n - 1 and a remainder r, such that
Clearly, A(x0) = r. Show how to compute the remainder r and the coefficients of q(x) in time
32.1-3
Derive a point-value representation for
32.1-4
Show how to use equation (32.5) to interpolate in time
32.1-5
Explain what is wrong with the "obvious" approach to polynomial division using a point-value representation. Discuss separately the case in which the division comes out exactly and the case in which it doesn't.
32.1-6
Consider two sets A and B, each having n integers in the range from 0 to 10n. We wish to compute the Cartesian sum of A and B, defined by
Note that the integers in C are in the range from 0 to 20n. We want to find the elements of C and the number of times each element of C is realized as a sum of elements in A and B. Show that the problem can be solved in O(n lg n) time. (Hint: Represent A and B as polynomials of degree 10n.)
In Section 32.1, we claimed that if we use complex roots of unity, we can evaluate and interpolate in
A complex nth root of unity is a complex number w such that
There are exactly n complex nth roots of unity; these are e2
Figure 32.2 shows that the n complex roots of unity are equally spaced around the circle of unit radius centered at the origin of the complex plane. The value
is called the principal nth root of unity; all of the other complex nth roots of unity are powers of wn.
The n complex nth roots of unity,
form a group under multiplication (see Section 33.3). This group has the same structure as the additive group (Zn, +) modulo n, since
Lemma 32.3
For any integers n
Proof The lemma follows directly from equation (32.6), since
Corollary 32.4
For any even integer n > 0,
Proof The proof is left as Exercise 32.2-1.
Lemma 32.5
If n > 0 is even, then the squares of the n complex nth roots of unity are the n/2 complex (n/2)th roots of unity.
Proof By the cancellation lemma, we have
Thus,
As we shall see, the halving lemma is essential to our divide-and-conquer approach for converting between coefficient and point-value representations of polynomials, since it guarantees that the recursive subproblems are only half as large.
Lemma 32.6
For any integer n
Proof Because equation (3.3) applies to complex values,
Requiring that k not be divisible by n ensures that the denominator is not 0, since
Recall that we wish to evaluate a polynomial
of degree-bound n at
The vector y = (y0, y1, . . . , yn-1) is the Discrete Fourier Transform (DFT) of the coefficient vector a = (a0, a1, . . . , an-1). We also write y = DFTn(a).
2The length n is actually what we referred to as 2n in Section 32.1, since we double the degree-bound of the given polynomials prior to evaluation. In the context of polynomial multiplication, therefore, we are actually working with complex (2n)th roots of unity.+
By using a method known as the Fast Fourier Transform (FFT), which takes advantage of the special properties of the complex roots of unity, we can compute DFTn(a) in time
The FFT method employs a divide-and-conquer strategy, using the even-index and odd-index coefficients of A(x) separately to define the two new degree-bound n/2 polynomials A[0](x) and A[1](x):
Note that A[0] contains all the even-index coefficients of A (the binary representation of the index ends in 0) and A[1] contains all the odd-index coefficients (the binary representation of the index ends in 1). It follows that
so that the problem of evaluating A(x) at
1. evaluating the degree-bound n/2 polynomials A[0](x) and A[1](x) at the points
and then
2. combining the results according to equation (32.9).
By the halving lemma, the list of values (32.10) consists not of n distinct values but only of the n/2 complex (n/2)th roots of unity, with each root occurring exactly twice. Therefore, the polynomials A[0] and A[1] of degree-bound n/2 are recursively evaluated at the n/2 complex (n/2)th roots of unity. These subproblems have exactly the same form as the original problem, but are half the size. We have now successfully divided an n-element DFTn computation into two n/2-element DFTn/2 computations. This decomposition is the basis for the following recursive FFT algorithm, which computes the DFT of an n-element vector a = (a0, a1, . . . , an - 1), where n is a power of 2.
The RECURSIVE-FFT procedure works as follows. Lines 2-3 represent the basis of the recursion; the DFT of one element is the element itself, since in this case
Lines 6-7 define the coefficient vectors for the polynomials A[0] and A[1]. Lines 4, 5, and 13 guarantee that w is updated properly so that whenever lines 11-12 are executed,
or, since
Lines 11-12 combine the results of the recursive DFTn/2 calculations. For y0, y1, . . . , yn/2 - 1, line 11 yields
where the last line of this argument follows from equation (32.9). For yn/2,yn/2+1, . . . , yn - 1, letting k = 0, 1, . . . , n/2 - 1, line 12 yields
The second line follows from the first since
To determine the running time of procedure RECURSIVE-FFT, we note that exclusive of the recursive calls, each invocation takes time
Thus, we can evaluate a polynomial of degree-bound n at the complex nth roots of unity in time
We now complete the polynomial multiplication scheme by showing how to interpolate the complex roots of unity by a polynomial, which enables us to convert from point-value form back to coefficient form. We interpolate by writing the DFT as a matrix equation and then looking at the form of the matrix inverse.
From equation (32.4), we can write the DFT as the matrix product y = Vna, where Vn is a Vandermonde matrix containing the appropriate powers of wn:
The (k, j) entry of
For the inverse operation, which we write as
Theorem 32.7
For j, k = 0, 1, . . . , n - 1, the (j, k) entry of
Proof We show that
This summation equals 1 if j' = j, and it is 0 otherwise by the summation lemma (Lemma 32.6). Note that we rely on -(n - 1) < j' - j < n - l, so that j' - j is not divisible by n, in order for the summation lemma to apply.
Given the inverse matrix
for j = 0,1, . . . , n - 1. By comparing equations (32.8) and (32.11), we see that by modifying the FFT algorithm to switch the roles of a and y, replace wn by
Thus, by using the FFT and the inverse FFT, we can transform a polynomial of degree-bound n back and forth between its coefficient representation and a point-value representation in time
Theorem 32.8
For any two vectors a and b of length n, where n is a power of 2,
where the vectors a and b are padded with 0's to length 2n and
32.2-1
Prove Corollary 32.4.
32.2-2
Compute the DFT of the vector (0, 1, 2, 3).
32.2-3
Do Exercise 32.1-1 by using the
32.2-4
Write pseudocode to compute
32.2-5
Describe the generalization of the FFT procedure to the case in which n is a power of 3. Give a recurrence for the running time, and solve the recurrence.
32.2-6
Suppose that instead of performing an n-element FFT over the field of complex numbers (where n is even), we use the ring Zm of integers modulo m, where m = 2tn/2 + 1 and t is an arbitrary positive integer. Use w = 2t instead of wn as a principal nth root of unity, modulo m. Prove that the DFT and the inverse DFT are well defined in this system.
32.2-7
Given a list of values z0, z1, . . . , zn-1 (possibly with repetitions), show how to find the coefficients of the polynomial P(x) of degree-bound n that has zeros only at z0, z1, . . . , zn - 1 (possibly with repetitions). Your procedure should run in time O(n lg2 n). (Hint: The polynomial P(x) has a zero at zj if and only if P(x) is a multiple of (x - zj).)
32.2-8
The chirp transform of a vector a = (a0, a1, . . . , an - 1) is the vector y = (y0, y1, . . . , yn - 1), where
to view the chirp transform as a convolution.)
Since the practical applications of the DFT, such as signal processing, demand the utmost speed, this section examines two efficient FFT implementations. First, we shall examine an iterative version of the FFT algorithm that runs in
We first note that the for loop of lines 10-13 of RECURSIVE-FFT involves computing the value
The operation in this loop, multiplying w (which is equal to
We now show how to make the FFT algorithm iterative rather than recursive in structure. In Figure 32.4, we have arranged the input vectors to the recursive calls in an invocation of RECURSIVE-FFT in a tree structure, where the initial call is for n = 8. The tree has one node for each call of the procedure, labeled by the corresponding input vector. Each RECURSIVE-FFT invocation makes two recursive calls, unless it has received a 1-element vector. We make the first call the left child and the second call the right child.
Looking at the tree, we observe that if we could arrange the elements of the initial vector a into the order in which they appear in the leaves, we could mimic the execution of the RECURSIVE-FFT procedure as follows. First, we take the elements in pairs, compute the DFT of each pair using one butterfly operation, and replace the pair with its DFT. The vector then holds n/2 2-element DFT's. Next, we take these n/2 DFT's in pairs and compute the DFT of the four vector elements they come from by executing two butterfly operations, replacing two 2-element DFT's with one 4-element DFT. The vector then holds n/4 4-element DFT's. We continue in this manner until the vector holds two (n/2)-element DFT's, which we can combine using n/2 butterfly operations into the final n-element DFT.
To turn this observation into code, we use an array A[0 . . n - 1] that initially holds the elements of the input vector a in the order in which they appear in the leaves of the tree of Figure 32.4. (We shall show later how to determine this order.) Because the combining has to be done on each level of the tree, we introduce a variable s to count the levels, ranging from 1 (at the bottom, when we are combining pairs to form 2-element DFT's) to lg n (at the top, when we are combining two (n/2)-element DFT's to produce the final result). The algorithm therefore has the following structure:
We can express the body of the loop (line 3) as more precise pseudocode. We copy the for loop from the RECURSIVE-FFT procedure, identifying y[0] with A[k . . k + 2s-1 _ 1] and y[1] with A[k + 2s-1. . k + 2s _ 1]. The value of w used in each butterfly operation depends on the value of s; we use wm, where m = 2s. (We introduce the variable m solely for the sake of readability.) We introduce another temporary variable u that allows us to perform the butterfly operation in place. When we replace line 3 of the overall structure by the loop body, we get the following pseudocode, which forms the basis of our final iterative FFT algorithm as well as the parallel implementation we shall present later.
We now present the final version of our iterative FFT code, which inverts the two inner loops to eliminate some index computation and uses the auxiliary procedure BIT-REVERSE-COPY(a, A) to copy vector a into array A in the initial order in which we need the values.
How does BIT-REVERSE-COPY get the elements of the input vector a into the desired order in the array A? The order in which the leaves appear in Figure 32.4 is "bit-reverse binary." That is, if we let rev(k) be the lg n-bit integer formed by reversing the bits of the binary representation of k, then we want to place vector element ak in array position A[rev(k)]. In Figure 32.4, for example, the leaves appear in the order 0, 4, 2, 6, 1, 5, 3, 7; this sequence in binary is 000, 100, 010, 110, 001, 101, 011, 111, and in bit- reverse binary we get the sequence 000, 001, 010, 011, 100, 101, 110, 111. To see that we want bit-reverse binary order in general, we note that at the top level of the tree, indices whose low-order bit is 0 are placed in the left subtree and indices whose low-order bit is 1 are placed in the right subtree. Stripping off the low-order bit at each level, we continue this process down the tree, until we get the bit-reverse binary order at the leaves.
Since the function rev (k) is easily computed, the BIT-REVERSE-COPY procedure can be written as follows.
The iterative FFT implementation runs in time
We can exploit many of the properties that allowed us to implement an efficient iterative FFT algorithm to produce an efficient parallel algorithm for the FFT. (See Chapter 29 for a description of the combinational-circuit model.) The combinational circuit PARALLEL-FFT that computes the FFT on n inputs is shown in Figure 32.5 for n = 8. The circuit begins with a bi-reverse permutation of the inputs, followed by lg n stages, each stage consisting of n/2 butterflies executed in parallel. The depth of the circuit is therefore
The leftmost part of the circuit PARALLEL-FFT performs the bit-reverse permutation, and the remainder mimics the iterative FFT-BASE procedure. We take advantage of the fact that each iteration of the outermost for loop performs n/2 independent butterfly operations that can be performed in parallel. The value of s in each iteration within FFT-BASE corresponds to a stage of butterflies shown in Figure 32.5. Within stage s, for s = 1, 2, . . . , lg n, there are n/2s groups of butterflies (corresponding to each value of k in FFT-BASE), with 2s-1 butterflies per group (corresponding to each value of j in FFT-BASE). The butterflies shown in Figure 32.5 correspond to the butterfly operations of the innermost loop (lines 8-11 of FFT-BASE). Note also that the values of w used in the butterflies correspond to those used in FFT-BASE: in stage s, we use
32.3-1
Show how ITERATIVE-FFT computes the DFT of the input vector (0, 2, 3, -1, 4, 5, 7, 9).
32.3-2
Show how to implement an FFT algorithm with the bit-reversal permutation occurring at the end, rather than at the beginning, of the computation. (Hint: Consider the inverse DFT.)
32.3-3
To compute DFTn, how many addition, subtraction, and multiplication elements, and how many wires, are needed in the PARALLEL-FFT circuit described in this section? (Assume that only one wire is needed to carry a number from one place to another.)
32.3-4
Suppose that the adders in the FFT circuit sometimes fail in such a manner that they always produce a zero output, independent of their inputs. Suppose that exactly one adder has failed, but that you don't know which one. Describe how you can identify the failed adder by supplying inputs to the overall FFT circuit and observing the outputs. Try to make your proeedure efficient.
32-1 Divide-and-conquer multiplication
a. Show how to multiply two linear polynomials ax + b and cx + d using only three multiplications. (Hint: One of the multiplications is (a + b)
b. Give two divide-and-conquer algorithms for multiplying two polynomials of degree-bound n that run in time
c. Show that two n-bit integers can be multiplied in O(n1g 3) steps, where each step operates on at most a constant number of 1-bit values.
32-2 Toeplitz matrices
A Toeplitz matrix is an n X n matrix A = (aij) such that aij = ai-1, j-1 for i = 2, 3, . . . , n and j = 2, 3, . . . , n.
a. Is the sum of two Toeplitz matrices necessarily Toeplitz? What about the product?
b. Describe how to represent a Toeplitz matrix so that two n X n Toeplitz matrices ean be added in O(n) time.
c. Give an O(n lg n)-time algorithm for multiplying an n X n Toeplitz matrix by a vector of length n. Use your representation from part (b).
d. Give an efficient algorithm for multiplying two n X n Toeplitz matrices. Analyze its running time.
32-3 Evaluating all derivatives of a polynomial at a point
Given a polynomial A(x) of degree-bound n, its tth derivative is defined by
From the coefficient representation (a0, a1, . . . , an-1) of A(x) and a given point x0, we wish to determine A(t) (x0) for t = 0, 1, . . . , n - 1.
a. Given coefficients b0, b1, . . . , bn-1 such that
show how to compute A(t) (x0), for t = 0, 1, . . . , n - 1, in O(n) time.
b. Explain how to find b0, b1, . . . , bn-1 in O(n lg n) time, given
c. Prove that
where f(j) = aj
d. Explain how to evaluate
32-4 Polynomial evaluation at multiple points
We have observed that the problem of evaluating a polynomial of degree-bound n - 1 at a single point can be solved in O(n) time using Horner's rule. We have also discovered that such a polynomial can be evaluated at all n complex roots of unity in O(n lg n) time using the FFT. We shall now show how to evaluate a polynomial of degree-bound n at n arbitrary points in O(n lg2 n) time.
To do so, we shall use the fact that we can compute the polynomial remainder when one such polynomial is divided by another in O(n lg n) time, a result that we assume without proof. For example, the remainder of 3x3 + x2 - 3x + 1 when divided by x2 + x + 2 is
Given the coefficient representation of a polynomial
a. Prove that A(x) mod (x - z) = A(z) for any point z.
b. Prove that Qkk(x) = A(xk) and that Q0,n-1(x) = A(x).
c. Prove that for i
d. Give an O(n lg2 n)-time algorithm to evaluate A(x0), A(x1), . . . , A(xn-1).
32-5 FFT using modular arithmetic
As defined, the Discrete Fourier Transform requires the use of complex numbers, which can result in a loss of precision due to round-off errors. For some problems, the answer is known to contain only integers, and it is desirable to utilize a variant of the FFT based on modular arithmetic in order to guarantee that the answer is calculated exactly. An example of such a problem is that of multiplying two polynomials with integer coefficients. Exercise 32.2-6 gives one approach, using a modulus of length
a. Suppose that we search for the smallest k such that p = kn + 1 is prime. Give a simple heuristic argument why we might expect k to be approximately lg n. (The value of k might be much larger or smaller, but we can reasonably expect to examine O(lg n) candidate values of k on average.) How does the expected length of p compare to the length of n?
Let g be a generator of
b. Argue that the DFT and the inverse DFT are well-defined inverse operations modulo p, where w is used as a principal nth root of unity.
c. Argue that the FFT and its inverse can be made to work modulo p in time O(n lg n), where operations on words of O(lg n) bits take unit time. Assume that the algorithm is given p and w.
d. Compute the DFT modulo p = 17 of the vector (0, 5, 3, 7, 7, 2, 1, 6). Note that g = 3 is a generator of
Press, Flannery, Teukolsky, and Vetterling[161, 162] have a good description of the Fast Fourier Transform and its applications. For an excellent introduction to signal processing, a popular FFT application area, see the text by Oppenheim and Willsky [153].
Cooley and Tukey [51] are widely credited with devising the FFT in the 1960's. The FFT had in fact been discovered many times previously, but its importance was not fully realized before the advent of modern digital computers. Press, Flannery, Teukolsky, and Vetterling attribute the origins of the method to Runge and König ( 1924).
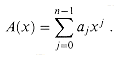
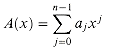
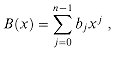
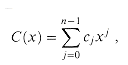
6x3 + 7x2 - 10x + 9
- 2x3 + 4x - 5
-------------------------
- 30x3 - 35x2 + 50x - 45
24x4 + 28x3 - 40x2 + 36x
- 12x6 - 14x5 + 20x4 - 18x3
---------------------------------------------
- 12x6 - 14x5 + 44x4 - 20x3 - 75x2 + 86x - 45

(32.1)

(32.2)
Note that degree(C) = degree(A) + degree(B), implying
degree-bound(C) = degree-bound(A) + degree-bound(B) - 1
 degree-bound(A) + degree-bound(B).
degree-bound(A) + degree-bound(B). (n2) time when the polynomials are represented in coefficient form, but only
(n2) time when the polynomials are represented in coefficient form, but only  (n) time when they are represented in point-value form. We can, however, multiply polynomials using the coefficient representation in only
(n) time when they are represented in point-value form. We can, however, multiply polynomials using the coefficient representation in only  (n lg n) time by converting between the two representations. To see why this works, we must first study complex roots of unity, which we do in Section 32.2. Then, we use the FFT and its inverse, also described in Section 32.2, to perform the conversions. Section 32.3 shows how to implement the FFT quickly in both serial and parallel models.
(n lg n) time by converting between the two representations. To see why this works, we must first study complex roots of unity, which we do in Section 32.2. Then, we use the FFT and its inverse, also described in Section 32.2, to perform the conversions. Section 32.3 shows how to implement the FFT quickly in both serial and parallel models.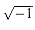 .
.32.1 Representation of polynomials
 (n lg n) time.
(n lg n) time.Coefficient representation
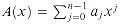 of degree-bound n is a vector of coefficients a = (a0, a1, . . ., an-1). In matrix equations in this chapter, we shall generally treat vectors as column vectors.
of degree-bound n is a vector of coefficients a = (a0, a1, . . ., an-1). In matrix equations in this chapter, we shall generally treat vectors as column vectors. (n) using Horner's rule:
(n) using Horner's rule:A(x0) = a0 + x0(a1+x0(a2+ ... +x0(an-2+x0(an-1))...)).
 (n) time: we just output the coefficient vector c = (c0, c1, . . ., cn-1), where cj = aj + bj for j = 0,1, . . . ,n - 1.
(n) time: we just output the coefficient vector c = (c0, c1, . . ., cn-1), where cj = aj + bj for j = 0,1, . . . ,n - 1. (n2), since each coefficient in the vector a must be multiplied by each coefficient in the vector b. The operation of multiplying polynomials in coefficient form seems to be considerably more difficult than that of evaluating a polynomial or adding two polynomials. The resulting coefficient vector c, given by equation (32.2), is also called the convolution of the input vectors a and b, denoted c = a
(n2), since each coefficient in the vector a must be multiplied by each coefficient in the vector b. The operation of multiplying polynomials in coefficient form seems to be considerably more difficult than that of evaluating a polynomial or adding two polynomials. The resulting coefficient vector c, given by equation (32.2), is also called the convolution of the input vectors a and b, denoted c = a  b. Since multiplying polynomials and computing convolutions are fundamental computational problems of considerable practical importance, this chapter concentrates on efficient algorithms for them.
b. Since multiplying polynomials and computing convolutions are fundamental computational problems of considerable practical importance, this chapter concentrates on efficient algorithms for them.Point-value representation
{(x0, y0), (x1, y1), . . ., (xn-1, yn-1)}yk = A(xk)
(32.3)
 (n2). We shall see later that if we choose the xk cleverly, this computation can be accelerated to run in time
(n2). We shall see later that if we choose the xk cleverly, this computation can be accelerated to run in time  (n lg n).
(n lg n).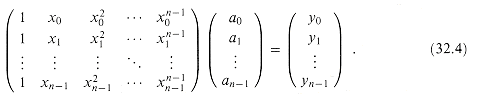
(32.4)
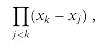
a = V(x0, x1, . . ., xn-1)-1y.

(32.5)
 (n2).
(n2). (n2).
(n2).{(x0, y0), (x1, y1), . . ., (xn-1, yn-1)} ,{(x0, y'0), (x1, y'1), . . ., (xn-1, y'n-1)}{(x0, y0 + y'0), (x1, y1+y'1), . . ., (xn-1, yn-1+y'n-1)}. (n).
(n).{(x0,y0),(x1, y1),...,(x2n-1,y2n-1)},{(x0,y'0),(x1,y'1),...,(x2n-1,y'2n-1)},{(x0,y0y'0),(x1,y1y'1),...,(x2n-1,y2n-1y'2n-1)}. (n), much less than the time required to multiply polynomials in coefficient form.
(n), much less than the time required to multiply polynomials in coefficient form.Fast multiplication of polynomials in coefficient form
 (n lg n) time. As we shall see in Section 32.2, if we choose "complex roots of unity" as the evaluation points, we can produce a point-value representation by taking the Discrete Fourier Transform (or DFT) of a coefficient vector. The inverse operation, interpolation, can be performed by taking the "inverse DFT" of point-value pairs, yielding a coefficient vector. Section 32.2 will show how the FFT performs the DFT and inverse DFT operations in
(n lg n) time. As we shall see in Section 32.2, if we choose "complex roots of unity" as the evaluation points, we can produce a point-value representation by taking the Discrete Fourier Transform (or DFT) of a coefficient vector. The inverse operation, interpolation, can be performed by taking the "inverse DFT" of point-value pairs, yielding a coefficient vector. Section 32.2 will show how the FFT performs the DFT and inverse DFT operations in  (n lg n) time.
(n lg n) time. (n lg n)-time procedure for multiplying two polynomials A(x) and B(x) of degree-bound n, where the input and output representations are in coefficient form. We assume that n is a power of 2; this requirement can always be met by adding high-order zero coefficients.
(n lg n)-time procedure for multiplying two polynomials A(x) and B(x) of degree-bound n, where the input and output representations are in coefficient form. We assume that n is a power of 2; this requirement can always be met by adding high-order zero coefficients.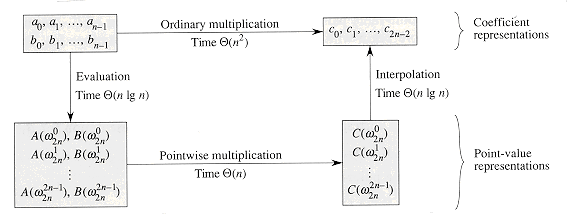
Figure 32.1 A graphical outline of an efficient polynomial-multiplication process. Representations on the top are in coefficient form, while those on the bottom are in point-value form. The arrows from left to right correspond to the multiplication operation. The w2n terms are complex (2n)th roots of unity.
 (n), and steps (2) and (4) take time
(n), and steps (2) and (4) take time  (n lg n). Thus, once we show how to use the FFT, we will have proven the following.
(n lg n). Thus, once we show how to use the FFT, we will have proven the following. (n lg n), with both the input and output representations in coefficient form.
(n lg n), with both the input and output representations in coefficient form. Exercises
A(x) = q(x)(x - x0) + r .
 (n) from x0 and the coefficients of A.
(n) from x0 and the coefficients of A.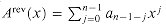 from a point-value representation for
from a point-value representation for 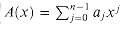 , assuming that none of the points is 0.
, assuming that none of the points is 0. (n2). (Hint: First compute
(n2). (Hint: First compute  j(x - xk) and
j(x - xk) and  j(xj - xk) and then divide by (x - xk) and (xj - xk) as necessary for each term. See Exercise 32.1-2.)
j(xj - xk) and then divide by (x - xk) and (xj - xk) as necessary for each term. See Exercise 32.1-2.)C = {x + y: x  A and y
A and y  B}.
B}.32.2 The DFT and FFT
 (n lg n) time. In this section, we define complex roots of unity and study their properties, define the DFT, and then show how the FFT computes the DFT and its inverse in just
(n lg n) time. In this section, we define complex roots of unity and study their properties, define the DFT, and then show how the FFT computes the DFT and its inverse in just  (n lg n) time.
(n lg n) time.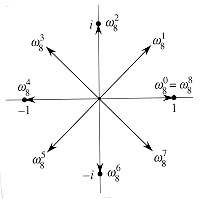
Figure 32.2 The values of
 in the complex plane, where w8 = e2
in the complex plane, where w8 = e2 i/8 is the principal 8th root of unity.
i/8 is the principal 8th root of unity.Complex roots of unity
wn = 1 .
 ik/n for k = 0, 1, . . . , n - 1. To interpret this formula, we use the definition of the exponential of a complex number:
ik/n for k = 0, 1, . . . , n - 1. To interpret this formula, we use the definition of the exponential of a complex number:eiu = cos(u) + i sin(u).
wn = e2
 i/n
i/n(32.6)
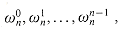
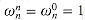 implies that
implies that 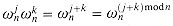 . Similarly,
. Similarly, 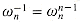 . Essential properties of the complex nth roots of unity are given in the following lemmas.
. Essential properties of the complex nth roots of unity are given in the following lemmas. 0, k
0, k  0, and d > 0,
0, and d > 0,
(32.7)

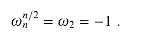
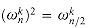 , for any non-negative integer k. Note that if we square all of the complex nth roots of unity, then each (n/2)th root of unity is obtained exactly twice, since
, for any non-negative integer k. Note that if we square all of the complex nth roots of unity, then each (n/2)th root of unity is obtained exactly twice, since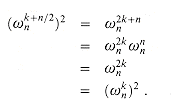
 have the same square. This property can also be proved using Corollary 32.4, since
have the same square. This property can also be proved using Corollary 32.4, since 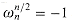 implies
implies 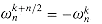 , and thus
, and thus 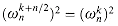 .
.  1 and nonnegative integer k not divisible by n,
1 and nonnegative integer k not divisible by n,
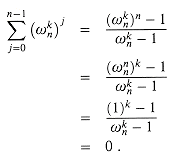
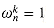 only when k is divisible by n.
only when k is divisible by n. The DFT
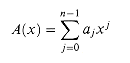
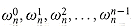 (that is, at the n complex nth roots of unity).2 Without loss of generality, we assume that n is a power of 2, since a given degree-bound can always be raised--we can always add new high-order zero coefficients as necessary. We assume that A is given in coefficient form: a = (a0, a1, . . . , an-1). Let us define the results yk, for k = 0, 1, . . . , n - 1, by
(that is, at the n complex nth roots of unity).2 Without loss of generality, we assume that n is a power of 2, since a given degree-bound can always be raised--we can always add new high-order zero coefficients as necessary. We assume that A is given in coefficient form: a = (a0, a1, . . . , an-1). Let us define the results yk, for k = 0, 1, . . . , n - 1, by
(32.8)
The FFT
 (n lg n), as opposed to the
(n lg n), as opposed to the  (n2) time of the straightforward method.
(n2) time of the straightforward method.A[0](x) = a0 + a2x + a4x2 +


 + an-2xn/2-1,
+ an-2xn/2-1,A[1](x) = a1 + a3x + a5x2 +


 + an-1xn/2-1.
+ an-1xn/2-1.A(x) = A[0](x2) + xA[1](x2),
(32.9)
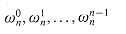 reduces to
reduces to
(32.10)
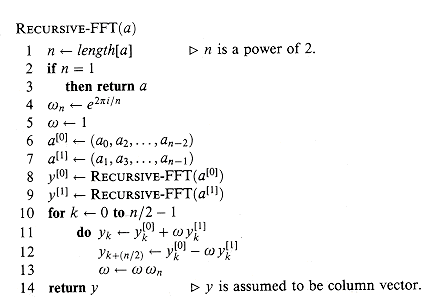
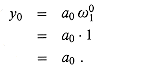
 . (Keeping a running value of w from iteration to iteration saves time over computing
. (Keeping a running value of w from iteration to iteration saves time over computing 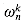 from scratch each time through the for loop.) Lines 8-9 perform the recursive DFTn/2 computations, setting, for k = 0, 1, . . . , n/2 - 1,
from scratch each time through the for loop.) Lines 8-9 perform the recursive DFTn/2 computations, setting, for k = 0, 1, . . . , n/2 - 1,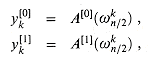
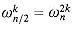 by the cancellation lemma,
by the cancellation lemma,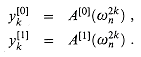
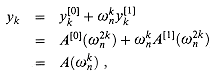
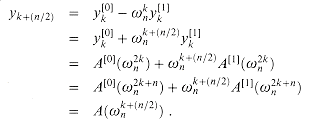
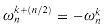 . The fourth line follows from the third because
. The fourth line follows from the third because  implies
implies 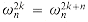 . The last line follows from equation (32.9). Thus, the vector y returned by RECURSIVE-FFT is indeed the DFT of the input vector a.
. The last line follows from equation (32.9). Thus, the vector y returned by RECURSIVE-FFT is indeed the DFT of the input vector a. (n), where n is the length of the input vector. The recurrence for the running time is therefore
(n), where n is the length of the input vector. The recurrence for the running time is thereforeT(n) = 2T(n/2) +
 (n)
(n)=
 (n lg n) .
(n lg n) . (n lg n) using the Fast Fourier Transform.
(n lg n) using the Fast Fourier Transform.Interpolation at the complex roots of unity
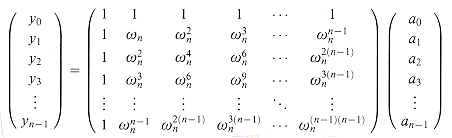
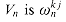 , for j,k = 0, 1, . . . , n - 1, and the exponents of the entries of Vn form a multiplication table.
, for j,k = 0, 1, . . . , n - 1, and the exponents of the entries of Vn form a multiplication table.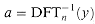 , we proceed by multiplying y by the matrix
, we proceed by multiplying y by the matrix 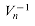 , the inverse of Vn.
, the inverse of Vn.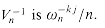 .
.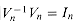 , the n X n identity matrix. Consider the (j, j') entry of
, the n X n identity matrix. Consider the (j, j') entry of 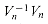 :
: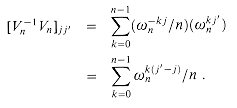
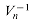 , we have that
, we have that  is given by
is given by
(32.11)
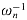 , and divide each element of the result by n, we compute the inverse DFT (see Exercise 32.2-4). Thus,
, and divide each element of the result by n, we compute the inverse DFT (see Exercise 32.2-4). Thus, 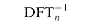 can be computed in
can be computed in  (n lg n) time as well.
(n lg n) time as well. (n lg n). In the context of polynomial multiplication, we have shown the following.
(n lg n). In the context of polynomial multiplication, we have shown the following.
 denotes the componentwise product of two 2n-element vectors.
denotes the componentwise product of two 2n-element vectors. Exercises
 (n lg n)-time scheme.
(n lg n)-time scheme. in
in  (n lg n) time.
(n lg n) time.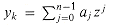 and z is any complex number. The DFT is therefore a special case of the chirp transform, obtained by taking z = wn. Prove that the chirp transform can be evaluated in time O(n lg n) for any complex number z. (Hint: Use the equation
and z is any complex number. The DFT is therefore a special case of the chirp transform, obtained by taking z = wn. Prove that the chirp transform can be evaluated in time O(n lg n) for any complex number z. (Hint: Use the equation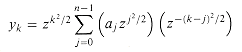
32.3 Efficient FFT implementations
 (n lg n) time but has a lower constant hidden in the
(n lg n) time but has a lower constant hidden in the  -notation than the recursive implementation in Section 32.2. Then, we shall use the insights that led us to the iterative implementation to design an efficient parallel FFT circuit.
-notation than the recursive implementation in Section 32.2. Then, we shall use the insights that led us to the iterative implementation to design an efficient parallel FFT circuit.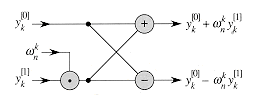
Figure 32.3 A butterfly operation. The two input values enter from the left,
 is multiplied by
is multiplied by 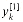 , and the sum and difference are output on the right. The figure can be interpreted as a combinational circuit.
, and the sum and difference are output on the right. The figure can be interpreted as a combinational circuit.
Figure 32.4 The tree of input vectors to the recursive calls of the RECURSIVE-FFT procedure. The initial invocation is for n = 8.
An iterative FFT implementation
 twice. In compiler terminology, this value is known as a common subexpression. We can change the loop to compute it only once, storing it in a temporary variable t.
twice. In compiler terminology, this value is known as a common subexpression. We can change the loop to compute it only once, storing it in a temporary variable t.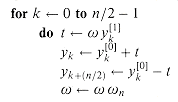
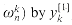 , storing the product into t, and adding and subtracting t from
, storing the product into t, and adding and subtracting t from  , is known as a butterfly operation and is shown schematically in Figure 32.3.
, is known as a butterfly operation and is shown schematically in Figure 32.3.1 for s
 1 to lg n
1 to lg n2 do for k
 0 to n - 1 by 2s
0 to n - 1 by 2s3 do combine the two 2s-1 -element DFT's in
A[k . . k + 2s-1 - 1] and A[k + 2s-1 . . k + 2s - 1]
into one 2s-element DFT in A[k . . k + 2s - 1]
FFT-BASE(a)
1 n
 length[a]
length[a]  n is a power of 2.
n is a power of 2.2 for s
 1 to lg n
1 to lg n3 do m
 2s
2s4 wm
 e2
e2 i/m
i/m5 for k
 0 to n - 1 by m
0 to n - 1 by m6 do w
 1
17 for j
 0 to m/2 - 1
0 to m/2 - 18 do t
 w A[k + j + m/2]
w A[k + j + m/2]9 u
 A[ k + j]
A[ k + j]10 A[k + j]
 u + t
u + t11 A[k + j + m /2]
 u - t
u - t12 w
 wwm
wwmITERATIVE-FFT(a)
1 BIT-REVERSE-COPY (a, A)
2 n
 length[a]
length[a] 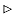 n is a power of 2.
n is a power of 2.3 for s
 1 to lg n
1 to lg n4 do m
 2s
2s5 wm
 e2
e2 i/m
i/m6 w
 1
17 for j
 0 to m/2 - 1
0 to m/2 - 18 do for k
 j to n - 1 by m
j to n - 1 by m9 do t
 w A[k + m/2]
w A[k + m/2]10 u
 A[k]
A[k]11 A[k]
 u + t
u + t12 A[k + m/2]
 u - t
u - t13 w
 wwm
wwm14 return A
BIT-REVERSE-COPY(a, A)
1 n
 length[a]
length[a]2 for k
 0 to n - 1
0 to n - 13 do A[rev(k)]
 ak
ak (n lg n). The call to BIT-REVERSE-COPY(a,A) certainly runs in O(n lg n) time, since we iterate n times and can reverse an integer between 0 and n - 1, with lg n bits, in O(lg n) time. (In practice, we usually know the initial value of n in advance, so we would probably code a table mapping k to rev(k), making BIT-REVERSE-COPY run in
(n lg n). The call to BIT-REVERSE-COPY(a,A) certainly runs in O(n lg n) time, since we iterate n times and can reverse an integer between 0 and n - 1, with lg n bits, in O(lg n) time. (In practice, we usually know the initial value of n in advance, so we would probably code a table mapping k to rev(k), making BIT-REVERSE-COPY run in  (n) time with a low hidden constant. Alternatively, we could use the clever amortized reverse binary counter scheme described in Problem 18-1.) To complete the proof that ITERATIVE-FFT runs in time
(n) time with a low hidden constant. Alternatively, we could use the clever amortized reverse binary counter scheme described in Problem 18-1.) To complete the proof that ITERATIVE-FFT runs in time  (n lg n), we show that L(n), the number of times the body of the innermost loop (lines 9-12) is executed, is
(n lg n), we show that L(n), the number of times the body of the innermost loop (lines 9-12) is executed, is  (n lg n). We have
(n lg n). We have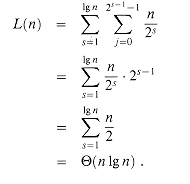
A parallel FFT circuit
 (lg n).
(lg n).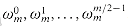 , where m = 2s.
, where m = 2s.
Figure 32.5 A combinational circuit PARALLEL-FFT that computes the FFT, here shown on n = 8 inputs. The stages of butterflies are labeled to correspond to iterations of the outermost loop of the FFT-BASE procedure. An FFT on n inputs can be computed in
 (1g n) depth with
(1g n) depth with  (n lg n) combinational elements.
(n lg n) combinational elements.Exercises
Problems
 (c + d).)
(c + d).) (n1g 3). The first algorithm should divide the input polynomial coefficients into a high half and a low half, and the second algorithm should divide them according to whether their index is odd or even.
(n1g 3). The first algorithm should divide the input polynomial coefficients into a high half and a low half, and the second algorithm should divide them according to whether their index is odd or even.

 for k = 0, 1, . . . , n - 1.
for k = 0, 1, . . . , n - 1.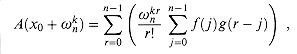
 j! and
j! and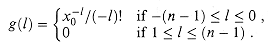
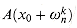 for k = 0, 1, . . . , n - 1 in O(n lg n) time. Conclude that all nontrivial derivatives of A(x) can be evaluated at x0 in O(n lg n) time.
for k = 0, 1, . . . , n - 1 in O(n lg n) time. Conclude that all nontrivial derivatives of A(x) can be evaluated at x0 in O(n lg n) time.(3x3 + x2 - 3x + 1) mod (x2 + x + 2) = 5x - 3.
 and n points x0, x1, . . . , xn-1, we wish to compute the n values A(x0), A(x1), . . . , A(xn-1). For 0
and n points x0, x1, . . . , xn-1, we wish to compute the n values A(x0), A(x1), . . . , A(xn-1). For 0  i
i  j
j  n - 1, define the polynomials
n - 1, define the polynomials 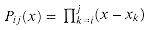 and Qij(x) = A(x) mod pij(x). Note that Qij(x) has degree-bound at most j - i.
and Qij(x) = A(x) mod pij(x). Note that Qij(x) has degree-bound at most j - i. k
k  j, we have Qik(x) = Qij(x) mod Pik(x) and Qkj(x) = Qij(x) mod Pkj (x).
j, we have Qik(x) = Qij(x) mod Pik(x) and Qkj(x) = Qij(x) mod Pkj (x). (n) bits to handle a DFT on n points. This problem gives another approach that uses a modulus of the more reasonable length O(lg n); it requires that you understand the material of Chapter 33. Let n be a power of 2.
(n) bits to handle a DFT on n points. This problem gives another approach that uses a modulus of the more reasonable length O(lg n); it requires that you understand the material of Chapter 33. Let n be a power of 2.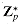 , and let w = gk mod p.
, and let w = gk mod p.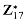 .
.Chapter notes