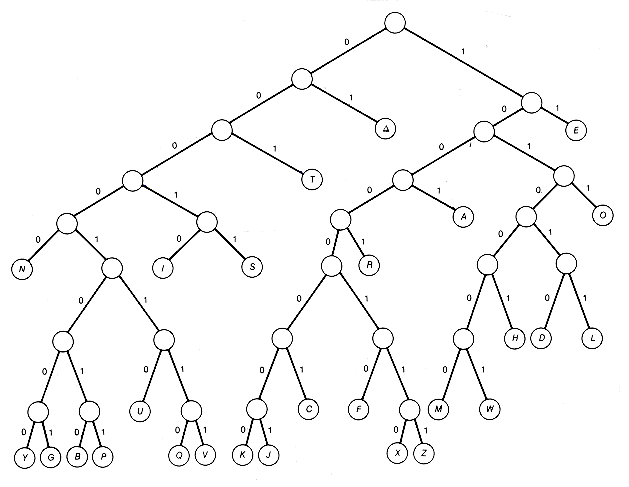
Figure 12.2 Binary Tree T1
Since elements of computer memory actually store only sequences of 0's and 1's (by design), character information must be encoded. One way to encode the character set of a computer is by means of a standard fixed-length code, which uses six 0's and 1's per character.
The character set of a computer is the alphabet of characters that it can accept. For example, not all computers accept braces (that is, {}). Two important standard character sets are ASCII (American Standard Code for Information Interchange) and EBCDIC (Extended Binary Coded Decimal Interchange Codes). Both use fixed-length codes. ASCII uses a seven-bit code and EBCDIC uses eight bits. An n-bit fixed-length code can distinguish 2n characters, and a sequence of l characters would then be represented by a sequence of l ?/FONT> n 0's and 1's. Variable-length codes are not constrained to using the same number of 0's and l's for each character.
Using a variable-length code, a text in which the characters occur with different frequencies can be compressed. Shorter-length sequences would be assigned to characters used more frequently, and longer-length sequences to characters used less frequently. This is the idea behind the Morse code. Morse, in fact, estimated the relative frequencies of characters by looking at the frequency with which printer's boxes containing the different characters of the alphabet needed to be refilled.
The use of fixed-length codes makes it easy to decode a sequence of 0's and 1's to recover the original sequence of characters or text. It is not so easy for variable-length codes. A variable-length code must be chosen with care, if it is to allow proper decoding and avoid ambiguity. One way to achieve such a code is to use the scheme outlined for Figure 12.2, which associates a code to each binary tree. Decoding the code generated by a given binary tree would then proceed as follows:
1. Start at the root of a binary tree that is identical to the one used for encoding the original text.
2. Follow the branches according to the dictates of the sequence of 0's and l's to be decoded梘o left for a 0 and right for a 1.
3. When a terminal node is reached, the sequence of 0's and 1's that led to it is decoded as the character associated with that terminal node.
4. Start again at the root to decode the remainder of the sequence in the same way.
The relative frequency with which each of twenty-six characters of the alphabet and the blank space between words occur in English text is as follows:
These relative frequencies are used to assign weights to the nodes of a tree such as T1. Each internal node is assigned weight 0, and each terminal node is assigned the relative frequency of the character associated with it. Thus, node S of T1 is assigned weight 51. The average amount of compression is measured by the weighted path length of the tree. In this way, the amount of compression achieved with different codes can be compared, since each tree has associated with it a unique code. The average length of the assigned codes is obtained by subtracting 1 from the weighted path length when the weights are normalized to sum to 1. Weights are normalized by dividing each weight by the sum of all the weights. The designer of a compression scheme can make this calculation directly or write a program for this purpose.
The weighted path length of T1 can be improved. Take the subtree with root at depth 5, and I and S as its successors, and interchange it with T to obtain binary tree T2 (shown in Figure 12.3). The weights of I and S, 57 and 51, will now each contribute one less time to the weighted path length of T2 than to T1, while T, with weight 80, will contribute one more time to the weighted path length of T2 than to T1. The result is that the weighted path length of T2 will be (57 + 51) - 80 less than that of T1.
The programmer's goal should be to find a binary tree, called the optimal binary tree, which has minimum weighted path length when the characters of the alphabet are stored at its n terminal nodes. Incidentally, the references here are to characters associated with the terminal nodes, but more generally they can be words or messages. A straightforward algorithm for finding this optimal binary tree is to generate each binary tree with n terminal nodes, associate the alphabetic characters with these n nodes, and calculate the weighted path length of the tree. A tree that yields the minimal weighted path length is optimal. Unfortunately, this algorithm is feasible only for small n. If n = 13, there are more than 1012 such trees, and the number of trees increases by a factor of almost 4 each time n increases by 1. We have to find a better way.
12.3.2 Representation of Huffman Trees
D A B C D E F G H I J K L
186 64 13 22 32 103 21 15 47 57 1 5 32
M N O P Q R S T U V W X Y Z
20 57 63 15 1 48 51 80 23 8 18 1 16 1
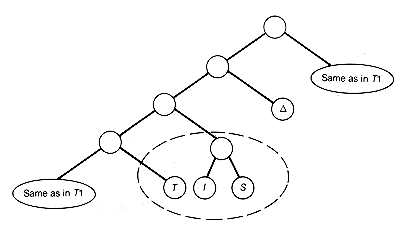
Figure 12.3 Binary Tree T2, Obtained by Interchanging Two Subtrees