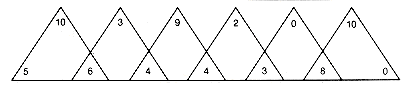
To start the development, we use the a's and b's of Example 12.3 and array them as shown in Figure 12.14(a). In an inorder traversal of any binary search tree with the six keys, the weights assigned to the accessed nodes would occur in the order a0 b1 a1 b2 a2 b3, and so on. This sequence looks like triples, as shown in Figure12.14(b). A value can be associated with each triple by summing up its weights. Thus the triples just shown have values 21, 13, 17, 9, 11, and 18 respectively. A greedy tree is constructed by always finding an allowed triple with minimal value and generating its corresponding subtree next. The weighted path length of the resultant tree is the sum of the weights of the (n - 1) triples thus created. The greedy construction procedure is as follows. The allowable triples shown in the array have values 21, 13, 17, 9, 11, and 18. The triple with the lowest value (9) is
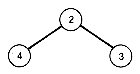
2
4 3
Combining the corresponding key and terminal nodes yields the subtree shown in Figure 12.14(c). Its assigned value is the triple value 9. Delete that triple from the array, and replace it by a terminal node value of 9, as shown in Figure 12.14(d).
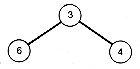
Now repeat this process. The next minimal value is 13, corresponding to the triple This gives the subtree shown in Figure 12.14(e). The condensed array is shown in Figure 12.14(f). Repeating the process finds the minimal triple whose value is 17. The corresponding subtree is Figure 12.14(g), and the new array is shown in Figure 12.14(h). Continuing in this fashion produces the arrays shown in Figure 12.14(i), (j), and (k).
3
6 4
b1 b2 b3 b4 b5 b6
10 3 9 2 0 10
5 6 4 4 3 8 0
a0 a1 a2 a3 a4 a5 a6

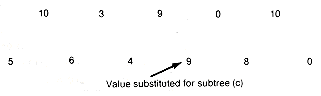
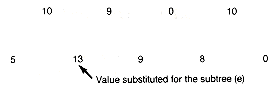

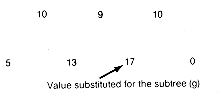
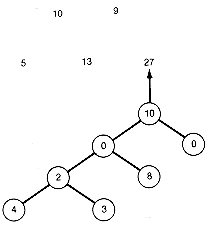
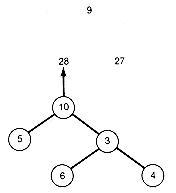

The greedy tree thus constructed by always taking a minimal triple is shown in Figure 12.15. Its weighted path length can be found by keeping an accumulated sum, as in the Huffman algorithm. In this case the greedy algorithm actually yields the optimal tree.